Class 11 Maths Chapter 10 Exercise 10.2

Class 11 Maths Chapter 10 Exercise 10.2 - Straight Lines NCERT Solutions

NCERT Solutions for Class 11 Maths Chapter 10, Exercise 10.2, provide a step-by-step explanation to help you understand the concepts of straight lines. These solutions have been crafted by an experienced CBSE maths teacher to ensure that students can easily grasp the methods. By studying the NCERT Solutions for Exercise 10.2, all your doubts related to Chapter 10 – Straight Lines will be cleared. Additionally, you can explore solutions for other exercises from Class 11 Maths Chapter 10 and other chapters to strengthen your understanding.

You can now Download the PDF of NCERT Solutions for Class 11 Maths Chapter 10, Exercise 10.2 on Straight Lines. This resource is specifically designed to help you easily understand and solve problems from Exercise 10.2 of Chapter 10, ensuring a better understanding of the concepts of straight lines and enhancing your performance in exams.

Q1. Write equations for the x and y axis.

Solution. Since ordinate (y coordinate) of every point on x-axis is 0,therefore the equation of x axis is y=0

Since ordinate (y coordinate) of every point on y axis is 0,therefore the equation of y axis is x =0

Q2.Find the equation of the line which passes through the point (-4,3) with slope 1/2.

Solution. The equation of a line which passes through (x1,y1) with slope m is given by

y – y1 = m(x -x1)

Here x1 =-4, y1 = 3 and m = 1/2

Putting these values in standard equation ,we get

y – 3 =( 1/2)[x -(-4)]

y -3 = (1/2) (x +4)

2y – 6 = x + 4

2y -x = 10

Hence required equation of the line is 2y -x =10

Q3. Find the equation of the line which passes through the origin(0,0) with slope m.

Solution. The equation of the line passes through the point(x1,y1) with slope m is given by

y -y1 = m(x – x1)

Here x1 = 0 ,y1 = 0 and m =m

y -0 = m(x -0)

y = mx

mx -y = 0

The required equation is mx -y = 0

Q4.Find the equation of the line which passes through (2,2√3) and is inclined with the x axis at an angle of 75°.

Solution. The equation of the line passes through the point(x1,y1) with slope m is given by

y -y1 = m(x – x1)

Here x1 = 2,y1 = 2√3 and m =tan 75°

tan 75°= tan (45 +30) = (tan 45 + tan30)/(1-tan 45 tan 30) = (1 + 1/√3)/(1 -1/√3) = (√3+1)/(√3-1)

∴ m = (√3+1)/(√3 -1)

Therefore putting the value of m in standard equation

y – 2√3 = (√3 +1)/(√3 -1)[x – 2]

(y -2√3)(√3 -1) = (√3+1)(x -2)

y√3 – y -6 +2√3 =x√3 -2√3+x -2

(√3 -1)y -(√3 -1)x =6-2 -2√3-2√3

(√3 -1)y -(√3 -1)x =4 -4√3

(√3 -1)x -(√3 -1)y=4√3-4

(√3 -1)x -(√3 -1)y=4(√3-1)

Hence the required equation passing through the given point is (√3 -1)x -(√3 -1)y=4(√3-1)

Q5. Find the equation of the line which intersects the x axis at a distance of 3 units to the left of origin with slope -2.

Solution. The coordinates of the point 3 units to the left of origin is (-3,0)

The slope of the line which is passing through (-3,0) is given = -2

The equation of the line passes through the point(x1,y1) with slope m is given by

y -y1 = m(x – x1)

Here x1 = -3,y1 = 0 and m= -2

y-0 = -2[x -(-3)]

y = -2x -6

2x +y +6 =0

Hence required equation is 2x +y +6 =0

Q6. Find the equation of the line which intersects the y axis at a distance of 2 units above the origin and makes an angle of 30° with the positive direction of the x axis.

Solution. The point on y axis which is at a distance of 2 units above the origin is (0,2)

The slope(m) of the line which is passing through (0,2) is, m = tan 30°=1/√3

The equation of the line passes through the point(x1,y1) with slope m is given by

y -y1 = m(x – x1)

Here x1 = 0,y1 = 2 and m= 1/√3

y -2 = (1/√3)(x – 0)

y -2 = x/√3

y√3 -2√3 = x

x -y√3 +2√3 =0

Q7. Find the equation of the line which passes through the points (–1, 1) and (2, – 4)

Solution. The given points are (-1,1) and (2,-4)

The equation of the line passing through the points (x1,y1) with slope m is given by

y -y1 =m (x -x1), where x1 =-1,y1=1 and x2 =2,y2 =-4

The slope m = (y2-y1)/(x2-x1) =(-4-1)/(2+1) = -5/3

∴ y -1 = (-5/3)(x +1)

3y -3 = -5(x +1)

3y -3 =-5x -5

5x +3y +2 = 0

Hence the required equation is 5x +3y +2 = 0

Q8. Find the equation of the line which is at a perpendicular distance of 5 units from the origin and the angle made by the perpendicular with the positive x-axis is 30^o.

Solution. The perpendicular distance(p) of the line from the origin = 5 units

Angle made by the perpendicular(w) with the positive x axis = 30°

The equation of a line which is at a perpendicular distance (p) from the origin and the angle(w) made by the perpendicular with the positive x -axis is given by

x cos ω + y sin ω = p

Putting the value ω = 30°

x cos 30° + y sin 30° = 5

x(√3/2) + y (1/2) = 5

x√3 + y = 10

x√3 + y – 10=0

Hence the required equation which is described in the question is

x√3 + y -10 = 0

Q9. The vertices of the ΔPQR are P(2,1), Q(-2,3) and R(4,5). Find equation of the median through the vertex R.

Solution. The vertices of the ΔPQR are P(2,1), Q(-2,3) and R(4,5) and median through the vertex are shown below

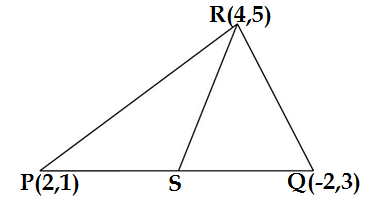
The coordinates of S are [(-2+2)/2, (3+1)/2] = (0,2)

y -y1 =m (x -x1), where x1 =4,y1=5 and x2 =-2,y2 =3

The slope(m) of the median (RS) of the ΔPQR is = (5-2)/(4-0) = 3/4

y -5=(3/4) (x -4)

4y -20 = 3x -12

3x -4y -12 +20 = 0

3x -4y + 8 = 0

Hence the required equation of the median RS of the ΔPQR is 3x -4y + 8 = 0

Q10.Find the equation of the line passing through (–3, 5) and perpendicular to the line through the points (2, 5) and (–3, 6).

Solution. Since two lines are perpendicular to each other when the product of their slopes

(m₁ and m₂) is

m₁m₂=-1

Let slope of the line which is passing through the given points (-3,5) =m₁and slope of the line joining two given points (2,5) and (-3,6)= m₂

We know slope(m) of the line which joins two points (x₁,y₁) and (x₂,y₂) is given by

m =(y₂-y₁)/(x₂-x₁)

m₂= (6-5)/(-3-2) = -1/5

m₁(-1/5)=-1

m₁=-1×-5 = 5

The equation of the line which is passing through a point (x₁,y₁) with slope m is given by

y – y₁=m (x -x₁)

The equation of the line which is passing through a point (-3,5) with slope 5 is given by

y -5 = 5(x +3)

y -5 = 5x +15

5x -y +20 = 0

Hence required equation of the line is 5x – y +20 =0

Q11. A line perpendicular to the line segment joining the points (1, 0) and (2, 3) divides it in the ratio 1: n. Find the equation of the line.

Solution. Let the coordinates of the point of intersection of a perpendicular line and line segment joining two points (x₁,y₁) and (x₂,y₂) are (x,y)

x = (kx₂+x₁)/(k+1) and y=(ky₂+y₁)/(k+1) where k is the ratio by which the point(x,y) divides the line segment

$x=\frac{2/n+1}{1/n +1},y=\frac{3/n+0}{1/n+1}$

$x=\frac{n+2}{n +1},y=\frac{3}{n+1}$

The equation of the line which is passing through a point (x₁,y₁) with slope m is given by

y – y₁=m (x -x₁)

Since two lines are perpendicular to each other when the product of their slopes

(m₁ and m₂) is

m₁m₂=-1 ,where m₂=(y₂-y₁)/(x₂-x₁)

∴m₁= (x₁-x₂)/(y₂-y₁)=(1-2)/(3-0) = -1/3

Therefore the equation of perpendicular line passes through [(n+2)/(n+1), 3/(n+1)] is given as

y -3/(n+1) = -1/3[x -(n+2)/(n+1)]

3y(n+1) -9= -[x(n +1)-(n+2)]

3y(n+1) -9 = -x(n+1) + n+2

3y(n+1) +x(n+1) = n+11

x(n+1) + 3y(n+1) -n -11 =0

Hence the required equation is x(n+1) + 3y(n+1) -n -11 =0

Q12.Find the equation of a line that cuts off equal intercepts on the coordinate axes and passes through the point (2, 3).

Solution. The equation of the line with x axis intercept a and y axis intercept b is given as

x/a + y/b = 1

Since it is given to us a = b,so putting the value of a and x =2,y = 3

2/b + 3/b = 1

5/b =1

b = 5

Also a = 5

Putting the values of a and b in the standard intercepts form of the equation

x/5 + y/5 = 1

x + y = 5

Hence the required equation is x+y =5

Q13. Find equation of the line passing through the point (2, 2) and cutting off intercepts on the axes whose sum is 9.

Solution. The equation of the line with x axis intercept a and y axis intercept b is given as

x/a + y/b = 1

The sum of the x intercept and y intercept given to us is a +b=9 so putting the value of a=9-b in the equation

x/(9-b)+ y/b = 1

Since the line is passing through (2,2)

2/(9-b)+ 2/b = 1

(2b + 18 -2b)/[b(9-b)] =1

18 = b(9- b)

9b -b² = 18

b²-9b + 18 = 0

b²-6b -3b + 18 =0

b(b -6) -3(b -6) = 0

(b -6)(b-3) = 0

b = 6,3

If b=6 then a = 9 -6 = 3 and if b= 3 then a = 9- 3 =6

Putting the values of a and b in the standard intercepts form of the equation

x/3 + y/6 = 1 or x/6 + y/3 =1

2x + y = 6 or x + 2y = 6

Hence the required equations are 2x + y = 6 or x + 2y = 6

Q14.Find the equation of the line through the point (0, 2) making an angle 2π/3 with the positive x-axis. Also, find the equation of line parallel to it and crossing the y-axis at a distance of 2 units below the origin.

Solution. The line described in the question is passing through the point (0,2) making an angle 2π/3 with the positive x axis means slope of the line,m = tan 2π/3

m = tan 2π/3 = tan (π – π/3) = -tan π/3= -√3 [ since tan 2π/3 lies in second quadrant where tan is negative)

The equation of the line which is passing through a point (x₁,y₁) with slope m is given by

y – y₁=m (x -x₁)

Therefore equation of the line passes through (0,2) is

y -2 = -√3(x -0)

y -2 = -x√3

x√3 + y -2 = 0

The second line which is parallel to the previous line crossing the y-axis at a distance of 2 units below the origin

Therefore coordinates of the point where the line crosses the y axis are (0,-2)

We know the slopes of two parallel lines are equal,so the slope of the line,m =-√3

The equation of the line which is passing through a point (x₁,y₁) with slope m is given by

y – y₁=m (x -x₁)

Therefore equation of the line passes through (0,-2) is

y +2 = -√3(x -0)

y +2 =-x√3

x√3 +y +2 =0

Hence equation of the line is x√3 + y -2 = 0 and equation of the line parallel to it is x√3 +y +2 =0

Q15. The perpendicular from the origin to a line meets it at the point (–2, 9), find the equation of the line.

Solution. We are given the perpendicular from the origin to a line that meets it at the point (–2, 9)

So, perpendicular on the line from the origin passes through (0,0) and (-2,9)

Therefore the slope of the perpendicular line,m is

m = (9-0)/(-2-0) = -9/-2 = 9/2

The equation of the line which is passing through a point (x₁,y₁) with slope m is given by

y – y₁=m (x -x₁)

It is known to us that the product of the slopes of two perpendicular lines is = -1

m ×9/2 = -1

m = -2/9

Therefore equation of the line passes through (-2,9) is

y +2 = -2/9(x -0)

9y +18 =-2x

2x + 9y +18 = 0

Hence the required equation of the line is 2x + 9y +18 = 0

Q16.The length L (in centimetre) of a copper rod is a linear function of its Celsius temperature C. In an experiment, if L = 124.942 when C = 20 and L= 125.134 when C = 110, express L in terms of C.

Solution. It is given to us that length, L is the function of Celsius, C

In an experiment, if L = 124.942 when C = 20 and L= 125.134 when C = 110

If L is shown along Y-axis and C is shown along X-axis, then we get two points in the XY plane (20,124.942) and (110,125.134)

Express L in terms of C, means we have to find out the equation of the line joining two points (20,124.942) and (110,125.134)

The equation of the line which is passing through a point (x₁,y₁) with slope m is given by

y – y₁=m (x -x₁)

m = (125.134 -124.942)/(110-20)=0.192/90

Putting the values of (20,124.942) in place of (x₁,y₁) [hint :you can put (110,125.134) also]

$y-124.942=\frac{0.192}{90}\left ( x-20 \right )$

90y -11244.78 = 0.192x -3.84

90y = 0.192x -3.84 +11244.78

90y = 0.192x +11240.94

Replacing y =L and x = C

90L = 0.192 C + 11240.94

$L=\frac{0.192}{90}C+11240.94$

Hence L is expressed in terms of the C by the relation

$L=\frac{0.192}{90}C+11240.94$

Q17.The owner of a milk store finds that, he can sell 980 litres of milk each week at Rs. 14/litre and 1220 litres of milk each week at Rs. 16/litre. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at Rs. 17/litre?

Solution. Let the demand is shown by x and selling price is shown by y axis

Therefore in XY plane there are two points (980,14) and (1220,16)

The slope,m of the line joining two points (980,14) and (1220,16)

m = (16 -14)/(1220 -980) = 2/240 = 1/120

The equation of the line which is passing through a point (x₁,y₁) with slope m is given by

y – y₁=m (x -x₁)

Putting the values (x₁,y₁) =(980,14) and m =1/120

$y-14=\frac{1}{120}\left ( x-980 \right )$

120y -1680 = x -980

x -120y =980 -1680

x -120y =-700

The relationship between demand(x) and selling price(y) is x -120y =700

If selling price(y) is Rs 17/litre ,so putting the value of y =17 in the equation

x-120×17 =-700

x-2040=-700

x = -700 + 2040 =1340

Hence the owner of the milk can sell 1340 litres at the selling price of Rs 17/litre

Q18.P (a, b) is the mid-point of a line segment between axes. Show that equation of the line is x/a + y/b = 2

Solution. The given point P(a,b) is the mid point of a line segment between axes

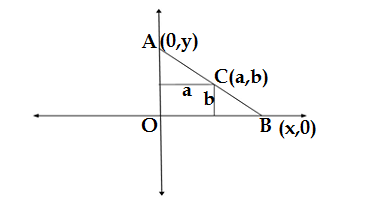
Let the line is AB which intersects the Y-axis at A and X-axis at B, the coordinates of A is (0,y) and coordinates of B are (x,0)

(0 +x)/2 =a and (y+0)/2 = b

x/2 =a and y/2 = b

x = 2a and y =2b

So, x-intercept is 2a and y-intercept is 2b

If x-intercept is a and y-intercept is b then the equation of the line is given by

x/a + y/b =1

Substituting a and b by 2a and 2b,we get required equation

x/2a + y/2b =1

x/a + y/b = 2

Hence proved

Q19. Point R (h, k) divides a line segment between the axes in the ratio 1: 2. Find the equation of the line.

Solution. It is given to us that point (h,k) divides a line segment between the X and Y-axis in the ratio of 1: 2

The coordinates of the points the line intersects y-axis is (0,y) and x-axis is (x,0)

According to section formula

$x=\frac{mx_{2}+nx_{1}}{m+n},y =\frac{my_{2}+ny_{_{1}}}{m+n}$

$h=\frac{x+2\times 0}{1+2}=\frac{x}{3},k=\frac{1\times 0+2y}{1+2}=\frac{2y}{3}$

x = 3h and y = 3k/2

Therefore the line is passing through the two points (0,3k/2) and (3h,0)

Slope of the line ,m = (0-3k/2)/(3h -0) = -3k/6h = -k/2h

The equation of the line which is passing through a point (x₁,y₁) with slope m is given by

y – y₁=m (x -x₁)

Therefore equation of the line passes through (3h,0)

y -0 = (-k/2h)(x – 3h)

y = (-k/2h) (x -3h)

2hy = -kx +3hk

2hy + kx -3hk =0

Q20. By using the concept of the equation of a line, prove that the three points (3, 0), (– 2, – 2) and (8, 2) are collinear.

Solution. Three given points are (3,0),(-2,-2) and (8,2)

The equation of the line which is passing through a point (x₁,y₁) with slope m is given by

y – y₁=m (x -x₁)

The slope of the line segment joining the two points (3,0) and (-2,-2) is

m=(-2-0)/(-2-3) = -2/-5 = 2/5

Putting the values for (x₁,y₁) =(3,0) and m =2/5

y – 0 = (2/5)(x -3)

5y = 2x -6

2x -5y -6 =0

For three points to be collinear the equation should satisfy the third point (8,2)

2×8 -5×2 -6 =0

16-10 -6 =0

16 -16 =0

0=0 ⇒LHS = RHS

Since (8,2) satisfy the equation of the line joining two points (3,0) and (-2,-2), therefore the given three points are collinear.

Class 11 Maths Exercise 10.2 of the chapter 10 Straight Lines consist of the questions based on the different straight lines passes through different points with different slopes in the cartesion planes.

The equation of the line that passes through the point (x₁,y₁) is given as

y-y₁= m( x-x₁)

Where m is the slope i.e tangent of the angle θ with the positive x-axis,m = tan θ

The slope of the line that passes through the points (x₁,y₁) and (x₂,y₂) is given by

$m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

The angle (θ) between two lines with slopes m₁ and m₂ given by

$tan\theta =\pm \left ( \frac{m_{2}-m_{1}}{1-m_{1}m_{_{2}}} \right )$

The coordinates of a point (x,y) which divides a line segment joining two points ( (x₁,y₁) and (x₂,y₂) in the ratio of m : n

$x=\frac{mx_{2}+nx_{1}}{m+n},y=\frac{my_{2}+ny_{1}}{m+n}$

We hope that Class 11 Maths Chapter 10 – Straight Lines Exercise 10.2 is now clearer to you. If you still have any questions or need further clarification about this exercise, don’t hesitate to ask in the comments. We’re here to help you succeed!

NCERT Solutions of Class 11 Maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability