Class 9 Maths Chapter 13 Exercise 13.9 - Surface Areas and Volumes NCERT Solutions

Class 9 Maths Chapter 13 Exercise 13.9 - Surface Areas and Volumes NCERT Solutions with PDF
The NCERT Solutions for Class 9 Maths Chapter 13 Exercise 13.9 on Surface Areas and Volumes are designed to help you grasp the key concepts of Geometry and apply relevant formulas effectively. These solutions break down complex problems into simple, understandable steps, making it easier for you to tackle application-level questions.
Created by experienced educators, these Class 9 Chapter 13 Maths Exercise 13.9 solutions follow the latest CBSE guidelines. They are presented in a clear, straightforward manner with easy-to-follow examples, ensuring that you are well-prepared for your Term 2 CBSE Board exam.
Download Class 9 Maths Chapter 13 Exercise 13.9 NCERT Solutions PDF
Download the Class 9 Maths Chapter 13 Exercise 13.9 NCERT Solutions PDF for Surface Areas and Volumes. This essential guide includes all the Class 9 Maths Chapter 13 Solutions, making it easier for you to complete your homework and prepare for exams effectively. The PDF format allows you to study offline, so you can access the Class 9 Chapter 13 Maths Solutions anytime, anywhere.
Class 9 Maths Chapter 13 - Surface Areas and Volumes: Find Links to All Exercises NCERT Solutions
Class 9 Maths Chapter 13 Exercise 13.9 - Surface Areas and Volumes NCERT Solutions
Q1. A wooden bookshelf has external dimensions as follows: Height = 110cm, Depth = 25cm,
Breadth = 85cm (see fig. 13.31). The thickness of the plank is 5cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2 and the rate of painting is 10 paise per cm2, find the total expenses required for polishing and painting the surface of the bookshelf.
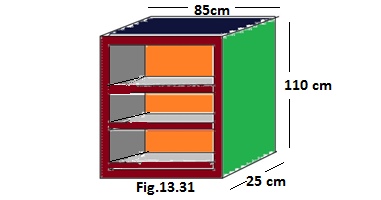
Solution. The external dimensions of the wooden bookshelf are
Height=110 cm, breadth =25 cm and depth of the wooden bookshelf is 85 cm
Let l=85 cm,b =25 cm and h=110 cm
Since thickness of the plank is 5 cm everywhere
Internal length(L) of front portion =85 -2×5 =85 -10 =75 cm
There are 4 planks in front portion
Total internal height of three self =110 -4×5 =90 cm
Hight(H) of single self =90/3 =30 cm
Breadh(B) of each self = 25 -5 =20 cm
Total external surface area of the bookself to be polished
= TSA of whole of bookself(as a cuboid) – 3×area of open portion of the bookself
=2(lb +bh +hl) – 3(length of each self×height of each self)
=2(85×25 +25×110+110×85) – 3(75×30)
=2(2125 +2750 +9350) – 3×2250
=2×14225 – 3×6750
=28450 – 6750
=21700
External Area to be polished is 21700 cm²
Cost of polishing is 20 paise per cm²
20 paise =Rs 0.20
Therefore cost of polishing external surface area of the bookself
= 21700×0.20
=4340
So, the cost of polishing is Rs 4340
Area of the bookshelf to be painted
= 3×TSA of single shelf(as a cuboid) -3×open area of each self
=3×2(LB +BH+HL) – 3(L×H)
=6(75×20+20×30 +30×75) -3(75×30)20100-6750
=6(1500 +600 +2250) -3(2250)
=6×4350 -6750
=26100-6750
=19350
Area to be painted is 19350 cm²
The cost of painting is 10 painse per cm²
10 painse =Rs 0.10
Therefore cost of painting is 0.10 ×19350 =Rs 1935
Total expenses required for polishing and painting the surface of the bookshelf
= Cost of polishing + Cost of painting
=Rs 4340 +Rs 1935
=Rs 6275
Hence total expenses of the painting and polishing is Rs 6275
Q2.The front compound wall of a house is decorated by wooden spheres of diameter 21 cm, placed on small supports as shown in fig. 13.32. Eight such spheres are used for this purpose, and are to be painted silver. Each support is a cylinder of radius 1.5cm and height 7cm and is to be painted black. Find the cost of paint required if silver paint costs 25 paise per cm2 and black paint costs 5 paise per cm2.

Solution. The diameter of the wooden sphere is 21 cm
The radius(r) of the wooden sphere is 21/2 =10.5 cm
Surface area of the sphere=4πr²
=4(22/7)×10.5×10.5
= 88 ×1.5×10.5
=1386
Surface area of a single sphere is 1386 cm²
Area of the sphere to be painted silver =Surface area of the sphere -area of lower circular end of the sphere attached to cynder = 1386 -πr²= 1386 -(22/7)×1.5×1.5 =1386 -7.07=1378.93
The surface area of 8 spheres to be painted =8×1378.93=11031.44 cm²
The cost of silver paint is 25 paise per cm²
35 paise =Rs 0.25
The cost of painting silver colour is
=0.25× 11031.44=Rs 2757.86
Area of the cylinder to be painted
= Curved surface area of the cylinder
=2πrh, where radius (r) of the cylinder is given 1.5 cm and height(h) is given 7 cm
=2(22/7)×1.5×7
= 44×1.5
=66
The surface area of 8 cylinders to be painted is 8×66 =528 cm²
The cost of black paint is 5 paise per cm²
5 paise =Rs 0.05
The cost of painting black colour is
=0.05×528
=Rs 26.40
The total cost of painting both colours
=Rs 2757.86 +Rs 26.40
= Rs 2784.26
Q3.The diameter of a sphere is decreased by 25%. By what percent does its curved surface area decrease?
Solution. Let diameter of the sphere is 2r then its radius is r
Its surface area is,S =4πr²
Since diameter of the sphere is decreased by 25% then diameter of modified sphere is
=2r -25% of 2r
= 2r – r/2
= (4r -r)/2 =3r/2
So, radius of the modified sphere is 3r/4
Surface area of the modified sphere is
S’=4π(3r/4)²=9πr²/4 cm²
The curved surface area of the sphere is decreased by
S -S’ =4πr² – 9πr²/4 =7πr²/4
The percent by which the curved surface area of the sphere is decreased
=[(S-S’)/S]×100
=6.25 ×7
=43.75 %
Hence curved surface area of the sphere is decreased by 43.75 %
The volume of the hemispherical bowl is 22.46 mm³
Conclusion - Class 9 Maths Chapter 13 Exercise 13.9 - Surface Areas and Volumes
Understanding Class 9 Maths Chapter 13 Exercise 13.9 is important for getting the hang of Surface Areas and Volumes. Our simple, step-by-step solutions for Class 9 Maths Chapter 13 Exercise 13.9 will help you work through each problem easily. With these solutions, Surface Areas and Volumes will feel much easier to learn. Be sure to download the PDF for Class 9 Chapter 13 Maths Exercise 13.9, so you can practice anytime and keep these key concepts handy. Keep practicing, and you’ll do great in your exams!
You Can Also Study
NCERT Solutions of class 9 maths
| Chapter 1- Number System | Chapter 9-Areas of parallelogram and triangles |
| Chapter 2-Polynomial | Chapter 10-Circles |
| Chapter 3- Coordinate Geometry | Chapter 11-Construction |
| Chapter 4- Linear equations in two variables | Chapter 12-Heron’s Formula |
| Chapter 5- Introduction to Euclid’s Geometry | Chapter 13-Surface Areas and Volumes |
| Chapter 6-Lines and Angles | Chapter 14-Statistics |
| Chapter 7-Triangles | Chapter 15-Probability |
| Chapter 8- Quadrilateral |
