NCERT solutions for class 9 maths chapter 10 circles
NCERT solutions for class 9 maths chapter 10 circles are important for all the students, study of these NCERT solutions is mandatory for all students of 9 class since examination papers are always prepared on the basis of the NCERT textbook. The proper understanding of these NCERT solutions of maths will help you in attempting the questions on your unit tests, half-yearly exams and annual exams.NCERT solutions for class 9 maths chapter 10 circles are created here by a step by step method therefore every student can understand the solutions easily.
Here you can study science and maths NCERT solutions from class 9 to 12, questions are explained by the depth of the concept in such a way that students could be access to the actual concept of the topics which is required to every student to get excellent marks in the exams. You can also study other extra study material like sample papers, previous years question papers solved and unsolved, preparation of competitive entrance exam.Here you can find the solutions of all exercises of chapter 10 Circles.
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
NCERT solutions for class 9 maths chapter 10 circles
Exercise 10.1
Exercise 10.2
Exercise 10.3
Exercise 10.4
Exercise 10.5
NCERT Solutions of class 9 maths
| Chapter 1- Number System | Chapter 9-Areas of parallelogram and triangles |
| Chapter 2-Polynomial | Chapter 10-Circles |
| Chapter 3- Coordinate Geometry | Chapter 11-Construction |
| Chapter 4- Linear equations in two variables | Chapter 12-Heron’s Formula |
| Chapter 5- Introduction to Euclid’s Geometry | Chapter 13-Surface Areas and Volumes |
| Chapter 6-Lines and Angles | Chapter 14-Statistics |
| Chapter 7-Triangles | Chapter 15-Probability |
| Chapter 8- Quadrilateral |
NCERT solutions for class 9 maths chapter 10 circles
Exercise 10.1
Q1.Fill in the blanks
(i) The centre of the circle lies in— of the circle .(exterior/interior)
(ii) A point, whose distance from the centre of a circle is greater than its radius lies in— of the circle.(exterior/interior)
(iii) The longest chord of the circle is a — of the circle.
(iv) An arc is — of a circle when its ends are the ends of a diameter.
(v) Segment of a circle is the region between an arc and— of the circle.
(vi) A circle divides the plane, on which it lies, in — parts.
Ans.(i) The centre of the circle lies in the interior of the circle.
(ii) A point, whose distance from the centre of a circle is greater than its radius lies in the exterior of the circle.
(iii) The longest chord of the circle is the diameter of the circle.
(iv) An arc is a semicircle of a circle when its ends are the ends of a diameter.
(v) Segment of a circle is the region between an arc and chord of the circle.
(vi) A circle divides the plane, on which it lies, in three parts.
Q2.Write true or false. Give reasons for your answers.
(i) Line segment joining the centre to any point on the circle is a radius of the circle.
(ii) A circle has only a finite number of equal chords.
(iii) If a circle is divided into three equal arcs, each is a major arc.
(iv) A chord of a circle, which is twice as long as its radius, is the diameter of the circle.
(v)Sector is the region between the chord and its corresponding arc.
(vi) A circle is a plane figure.
Ans.(i) True: All point on the circle are equidistant from the centre of the circle
(ii) False: A chord is a distance between two points on the circle, in the circle, there are infinite points and thus can have an infinite number of equal chords.
(iii) False : Each part is one-third of the circle, therefore can’t be a major arc.
(iv) True : Diameter is the longest chord of the circle ,diameter = 2× radius
(v) False: Sector is the region between two radii and an arc.
(vi) True: A circle is drawn on a plane, therefore it is a plane figure.
NCERT solutions for class 9 maths chapter 10 circles
Exercise 10.2
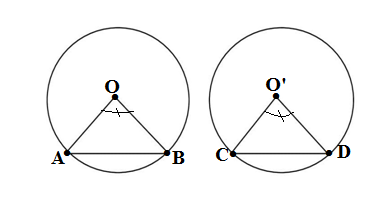
Q1. Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
Ans.
GIVEN: Two circles with equal radii with centre O and O’ and have equal chords AB =CD
TO PROVE: ∠AOB = ∠CO’D
PROOF: AO = CO’ ( radii of congruent circles)
BO = DO’ ( radii of congruent circles)
AB = CD ( given)
ΔAOB ≅ ΔCO’D (SSS rule)
∠AOB = ∠CO’D ( by CPCT rule)
Q2.Prove that, if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Ans.
GIVEN: Two circles with equal radii with centre O and O’ and have equal angles subtended at the centres by the chords ∠AOB = ∠CO’D
TO PROVE: AB = CD
PROOF: AO = CO’ ( radii of congruent circles)
BO = DO’ ( radii of congruent circles)
∠AOB = ∠CO’D ( given)
ΔAOB ≅ ΔCO’D (SAS rule criteria)
AO = CO’ ( by CPCT rule)
NCERT solutions for class 9 maths chapter 10 circles
Exercise 10.3
Q1.Draw different pair of circles. How many points does each pair have in common? What is the maximum number of common points?
Ans.Drawing circles of different types of pairs as following
It can be observed that three types of the possible pairs of the circles can be drawn which are shown by (i),(ii) and (iii)
(i) has no common points,(ii) has one common point and (iii) has two common points
Thus a pair of circles can have the maximum number of 2 common points.
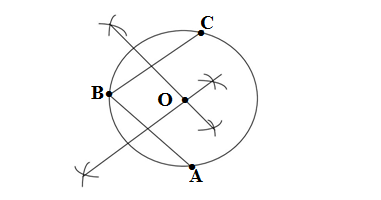
Q2. Suppose you are given a circle, give a construction to find its centre.
Ans.Construction for finding the centre of the circle
Step 1: Drawing two chords AB and BC such that one is the common point between them
Step 2:Drawing a perpendicular bisection of both chords AB and BC, both the perpendicular bisection of the chords intersect at a point located at the interior of the circle, this point O is the centre of the circle.
Q3.If two circles intersect at two points, prove that their centre lies on the perpendicular bisector of the common chord.
Ans.
GIVEN: Two circles with centre O and O’ and common chord AB,M is the point of intersection of the chord and the line OO’.
TO PROVE: OO’ is the perpendicular bisector of the common chord AB
Construction: Joining O to O’,A to O,O to B,A to O’ and B to O’
PROOF:In ΔOAO’ and ΔOBO’
OA = OB (radii of same circle)
O’A = O’B(radii of same circle)
OO’ = O’O(common)
ΔOAO’ ≅ ΔOBO’ (by SSS rule)
∠AOM = ∠BOM (by CPCT)
In ΔOAM and ΔOBM
OA = OB (radii of same circle)
OM = MO(common)
∠AOM = ∠BOM (proved above)
AM = BM (by CPCT)………(i)
∠AMO = ∠BMO (by CPCT)
∠AMO + ∠BMO =180 (linear pair)
∠AMO +∠AMO =180
2∠AMO = 180
∠AMO = 90°……………(ii)
Equation (i) and (ii) shows that O and O’ lies on the perpendicular bisector of the common chord AB
NCERT solutions for class 9 maths chapter 10 circles
Exercise 10.4
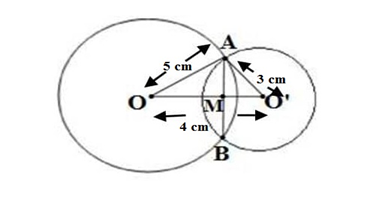
Q1.Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Ans. We are given two circles of centres O and O’ with radii 5 cm and 3 cm intersected at two points A and B.
Also given the distance between their centre OO’ = 4 cm
Let’s find out the length of the common chord
According to Heron’s formula the area of ΔAOO’
S = (a+b+c)/2 = (5+4+3)/2 = 6
…(i)
If two circles intersect at two points then the line joining the centres of the circles is the perpendicular bisector of the common chord of both circles.
Area of ΔAOO’ = 1/2(OO’×AM) = 1/2(4×AM)..(ii)
Therefore from both of the equations (i) and (ii)
1/2(4×AM) = 6
2AM = 6⇒ AM = 3 cm
Hence AB = 2AM = 2×3 = 6 cm
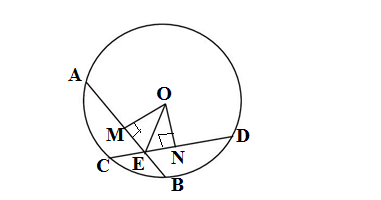
Q2.If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Ans.
GIVEN: A circle with centre O, two equal chords AB and CD intersecting to each other at E.
TO PROVE: AE = DE and BE =CE
CONSTRUCTION: Drawing OM⊥AB and ON⊥CD and Joining O to E
PROOF: Considering ΔOME and ΔONE
OM = ON (distance of equal chords from the centre)
∠OME = ∠ONE=90° (OM⊥AB and ON⊥CD)
OE = OE (common)
ΔOME ≅ΔONE (RHS principle)
ME = NE (by CPCT)……..(i)
It is given to us that
AB = CD
AB/2 = CD/2
Since perpendicular from centre to a chord bisects the chord
AM = DN……….(ii)
Adding both the equation (i) and equation (ii)
AM + ME = DN + NE
AE = DE,Hence proved
Subtracting both sided from AB
BE=AB -AE and CE= CD -DE= AB-AE
∴ BE = CE,Hence proved
Q3.If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Ans.
GIVEN: A circle with centre O, two equal chords AB and CD intersecting to each other at E.
TO PROVE: ∠OEM =∠OEN
CONSTRUCTION: Drawing OM⊥AB and ON⊥CD and Joining O to E
PROOF:In ΔOME and ΔONE
OM = ON (distance of equal chords from the centre)
∠OME = ∠ONE=90° (OM⊥AB and ON⊥CD)
OE = OE (common)
ΔOME ≅ΔONE (RHS principle)
∠OEM =∠OEN (by CPCT rule),Hence proved
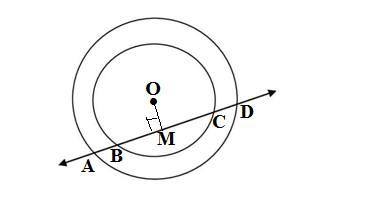
Q4.If a line intersects two concentric circles (circles with the same centres) with centre O at A, B, C and D prove that AB = CD (see figure).
Ans.
GIVEN: Two concentric circles with centre O, a line intersects both circles at A, B, C and D
TO PROVE: AB = CD
CONSTRUCTION: Drawing OM⊥ BC
PROOF: Since perpendicular from centre to a chord bisects the chord
OM⊥ BC (constructed)
∴BM = CM……..(i)
A, B, M,C and D lie on the same line
∴ OM⊥ AD
Since perpendicular from centre to a chord bisects the chord
∴AM = DM………(ii)
Subtracting equation (i) from equation (ii)
AM -BM = DM-CM
AB = CD, Hence proved
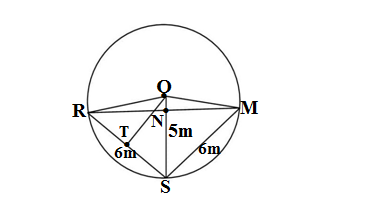
Q5.Three girls Reshma, Salma and Mandeep are playing a game by standing on a circle of radius 5 m drawn in a park. Reshma throws a ball to Salma, Salma to Mandeep, Mandeep to Reshma. If the distance between Reshma and Salma and between Salma and Mandeep is 6m each, what is the distance between Reshma and Mandeep?
Ans.It is given to us that three girls Reshma(R), Salma(S) and Mandeep(M) are located on a circle of radius 5 m such that RS =SM = 6m
In ΔORN and ΔOMN
∠ROS = ∠MOS (equal chords of a circle subtends equal angles to the centre)
OR = OM(radii of the same circle)
ON = ON(common)
ΔORN ≅ ΔOMN (SAS rule)
RN = MN (by CPCT)
∴RM = 2RN……(i)
∠ONR = ∠ONM(by CPCT
∠ONR + ∠ONM = 180° (linear pair)
2∠ONR = 180°
∠ONR = 90°
∴ RN ⊥OS
Area of the ΔROS =1/2(OS ×RN) = 5/2(RN)…..(ii)
Drawing OT⊥RS
∴TR =RS/2 =6/2 =3 m (perpendicular drawn from centre to chord bisects the chord)
OT =√(OR²-TR²) = √(5²-3²) =√(25-9) =√16 = 4 m (since OR =radius =5 m)
Area of the ΔROS =1/2(RS ×OT) = 1/2(6×4)=12 …..(iii)
From equation (ii) and equation (iii)
5/2(RN) = 12
RN = 24/5 = 4.8 m
From equation (i)
RM = 2 ×4.8 = 9.6 m
Hence the distance between Reshma and Mandeep is 9.6 m.
Q6.A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distances on its boundary each having a toy telephone in his hands to talk to each other. Find the length of the string of each phone.
Ans.We are given that three boys,Ankur(A),Syed(S) and David (D) are positioned on a circular park with radius 20 m such that AS = DS = AD
Drawing DM⊥ AS
∴AM = SM (Perpendicular drawn from the centre to the chord bisects the chord)
Since equilateral Δ ASD circumscribed by the circle with centre O,therefore O will also be the centroid of the circle.
We know the centroid of the circle divides the median into the ratio of 2:1
Let the length of the median DM is = x
Since DO:MO = 2: 1
Let the DO = 2k and MO = k
DO =20,therefore k = 10
MO =10 m
SM = √(OS²-MO²) = √(20²-10²) =√(400-100)=√(300) =10√3 m
Hence AS = 2SM =2×10√3 m=20√3 m
Therefore,the length of each string is 20√3 m
Exercise 10.5
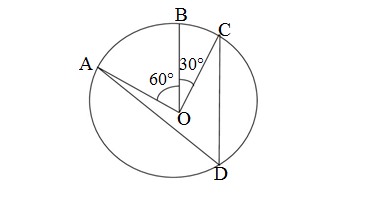
Q1. In figure A, B and C are three points on a circle with centre O such that ∠BOC = 30° and ∠AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.
Ans.It is given to us a circle with centre O
From the figure we have
∠AOB = 60° and ∠BOC = 30°
∴ ∠AOC = ∠AOB+ ∠BOC = 60° + 30° = 90°
Since angle subtended by an arc at the circle is half of the angle subtended by it at the centre
∠ADC = 1/2(∠AOC) = 1/2(90° ) = 45°
Q2.A chord of circle is equal to the radius of the circle, find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Ans.
We are given a circle with centre O in which
The chord AC = Radius of the circle
OA and OC are the radii of the circle
∴ AC = OA = OC
Since ΔAOC is the equilateral triangle, therefore each angle is 60°
∠AOC =60°
The angle on the minor arc is ∠ABC and the angle subtended by the given chord AC at the centre is ∠AOC
We know the angle subtended by an arc at the circle is half of the angle subtended by it at the centre.
Here the angle subtended by an arc ABC at the centre is reflex ∠AOC
reflex ∠AOC = 360° – 60° = 300°
∠ABC = 1/2(reflex∠AOC) = 300°/2 = 150°
On the same way, since the angle subtended by an arc at the circle is half of the angle subtended by it at the centre.
Therefore,
∠ADC = 1/2(∠AOC) = 60°/2 = 30°
Hence, the angle subtended by the chord at a point on the minor arc is 150° and at a point on the major arc is 60°
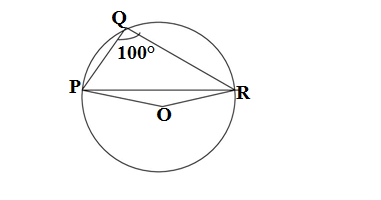
Q3.In figure ∠PQR = 100°,where P,Q and R are points on a circle with centre O. Find ∠OPR.
We are given ∠PQR = 100°, where P,Q and R are points on a circle
The angle subtended by a chord at the circle is half of the angle subtended by it at the centre.
The angle subtended by the chord PR at the centre is reflex ∠POR and at the circle is ∠PQR=100°
reflex ∠POR = 2∠PQR = 2×100 =200°
∴∠POR = 360°-reflex ∠POR = 360°-200° = 160°
In ΔPOR
PO = OR (radii of the circle)
∠OPR = ∠ORP (opposite angles of equal sides in a triangle)
According to the angle sum property of the triangle
∠OPR + ∠ORP +∠POR = 180°
∠OPR + ∠OPR +160°= 180°
2∠OPR = 180°- 160° =20°
∠OPR = 20°/2 = 10°
Therefore the required value of ∠OPR is 10°
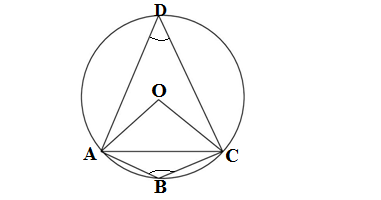
Q4.In figure ∠ABC =69°,∠ACB =31°,find ∠BDC.
In the figure,we are given ∠ABC =69° and ∠ACB =31°
Applying the angle sum property of the triangle
∠BAC +∠ABC +∠ACB =180°
∠BAC + 69° +31° = 180°
∠BAC + 100° = 180°
∠BAC = 180° – 100° =80°
Since,the angles made on the same segment are equal
∴∠BDC=∠BAC =80°
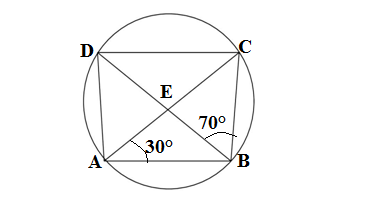
Q5. In figure A,B,C and D are four points on a circle .AC and BD intersects at point E such that ∠ BEC =130° and ∠ECD =20°.Find ∠BAC .
Ans.It is given to us that A, B, C and D are four points on a circle.AC and BD intersect at point E such that ∠ BEC =130° and ∠ECD =20°
∠DEC +∠BEC= 180° (∠DEC and ∠BEC are linear pair)
∠DEC +130°=180°
∠DEC= 180° – 130°= 50°
According to angle sum property of the triangle
∠DEC +∠EDC+∠ECD =180°
50°+∠EDC +20° = 180°
∠EDC = 180°- 70° = 110°
Since ∠EDC =∠BAC (angles made on the same segment)
Therefore ∠BAC = 110°
Q6.ABCD is a cyclic quadrilateral whose diagonals intersects at a point E .If ∠DBC =70°,∠BAC =30°,find ∠BCD.Further ,if AB =BC ,find ∠ECD.
Ans. It is given to us that ABCD is a cyclic quadrilateral whose diagonals intersects at a point E such that ∠DBC =70°,∠BAC =30°
From the figure it is clear that
∠BDC = ∠BAC (angles made on the same segment by the same chord BC)
∠BDC = 30°
∠DBC = ∠DAC (angles made on the same segment by the same chord DC)
∠DAC = 70°
∠DAB = ∠DAC +∠BAC = 70°+ 30° =100°
Since in a cyclic quadrilateral sum of opposite angles is 180°
∠DAB + ∠BCD = 180°
100° + ∠BCD = 180°
∠BCD = 180° – 100°
∠BCD=80°
If AB =BC then in ΔABC,we have
∠BAC = ∠ACB =30° (equal angles to opposite equal sides)
It is also clear from the figure
∠ECD = ∠DCB – ∠ACB
∠ECD = 80° – 30°
∠ECD = 50°
Q7.If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Ans.
GIVEN: ABCD is a cyclic quadrilateral and its diagonal AC and BD are the diameters of the circle.
TO PROVE: ABCD is a rectangle
PROOF: Since it is given to us that diagonals of cyclic quadrilateral ABCD are diameter of the circle
Therefore
∠BAD = 90°(angles made on a semicircle)
∠ABC = 90°(angles made on a semicircle)
∠BCD = 90°(angles made on a semicircle)
∠ADC = 90°(angles made on a semicircle)
Each angle ∠BAD,∠ABC ,∠BCD and ∠ADC is a right angle, therefore cyclic quadrilateral ABCD is a rectangle.
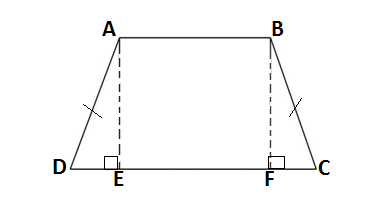
Q8. If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Ans.
GIVEN: ABCD is a trapizium in which AB is parallel to DC
AD = BC
TO PROVE: ABCD is a cyclic
CONSTRUCTION: Drawing AE ⊥ AB and BF ⊥ AB
PROOF: In ΔADE and ΔBCF
AD = BC (given)
∠AED = ∠BEC (each 90°)
Since AE ⊥ AB and BF ⊥ AB and AB parallel to DC
∴ AE ⊥ DC and BF ⊥ DC
Hence ABCD is a rectangle
∴ AE = BF (opposite sides of rectangle)
Therfore
ΔADE ≅ ΔBCF (RHS rule)
∠D = ∠C (by CPCT)
∠A + ∠D = 180° (sum of cointerior angles)
∠A = 180°- ∠D ….(i)
Since ∠C = ∠D ……(ii) (proved above)
Adding equation (i) and equation (ii)
∠A + ∠C = 180°- ∠D + ∠D = 180°
Therefore ABCD is a cyclic quadrilateral
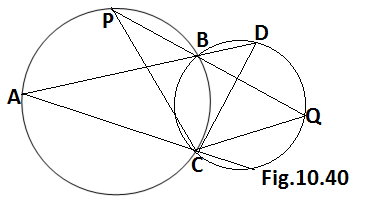
Q9. Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Fig. 10.40). Prove that ∠ ACP = ∠ QCD.
Ans.
GIVEN:Two circles intersects at two points B and C and two line segments ABD and PBQ two line segments intersects the circles at A, D and P,Q respectively
TO PROVE: ∠ ACP = ∠ QCD
PROOF: In circle PBCA
∠ACP = ∠ABP …(i)(angles made on same segment )
∠ABP = ∠DBQ ….(ii)(vertically opposite angle where ABD and PBQ are the lines)
∠DBQ = ∠QCD …..(iii)(angles made on same segment )
From equation (i),(ii) and (iii),we have
∠ACP = ∠ABP = ∠DBQ =∠QCD
∴∠ACP =∠QCD, Hence proved
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions of class 9 science
CBSE Class 9-Question paper of science 2020 with solutions
CBSE Class 9-Sample paper of science
CBSE Class 9-Unsolved question paper of science 2019
NCERT Solutions of class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT solutions of class 10 science
Solutions of class 10 last years Science question papers
CBSE Class 10 – Question paper of science 2020 with solutions
CBSE class 10 -sample paper of science
NCERT solutions of class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions of class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |