NCERT Solutions of class 9 Maths exercise 5.1 -Introduction to Euclid’s Geometry
NCERT Solutions of class 9 Maths exercise 5.1 of chapter 5-Introduction to Euclid’s Geometry.NCERT Solutions for class 9 maths exercise 5.1 chapter 5 -Introduction to Euclid’s Geometry are created for the class 9 CBSE maths students in helping their maths test and the CBSE maths exam. Class 9 maths chapter 5 Introduction to Euclid’s Geometry NCERT solutions are the most helpful tool in clearing the concept of Euclid’s Geometry.
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
Q1.Which of the following statements are true and which are false?Give reasons for your answers.
(i) Only one line can pass through a single point.
(ii) There are an infinite number of lines that pass through two district points.
(iii)A terminated line can be produced indefinitely on both sides.
(iv) If two circles are equal, then their radii are equal.
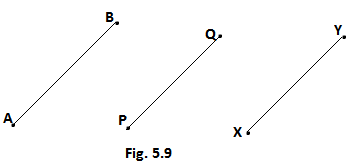
(v) In fig. 5.9,if AB = PQ and PQ = XY,then AB = XY.
Ans.(i) Infinite lines can pass through a point,so the given statement is false.
(ii) One unique line can be drawn through two distinct points,so given statement is false.
(iii) A terminated line is of definite length, so it can not be extended from either of the ends, so the given statement is wrong.
(iv) Two circles are equal means the circumference and centre of both circles coincide to each other,so let their radii are R1 and R2⇒ 2πR1 =2πR2⇒ R1 = R2, So, it is true.
(v) In fig.if AB = PQ,XY = PQ, then AB = XY, according to Euclid’s first axiom things which are equal to the same thing are also equal to each other,so the given statement is true.
Q2. Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they and how might you define them?
(i) Parallel lines
(ii)Perpendicular lines
(iii)Line segment
(iv)Radius of circle
(v)Square
Ans. For defining the given terms we need to be defined first the following terms.
Point: The point is a dot marked by a pencil or pen for showing the position,it is dimensionless.
Line: A line is a straight one-dimensional figure,a line has no thickness and can be extended both sides indefinitely,a line has no endpoints.
Plane: A plane is a flat surface covered by lines or curves,as an example surface of a paper sheet.
Ray: A ray is a part of a line that has only one endpoint, a ray can be extended one side only.
Angle: The angle is the figure formed by two rays with a common initial point, the measurement of the inclination of both rays is measured in degree.
Circle: A circle is a round figure that has no edges and corner point,the distance of all points on its boundary are located at the same distance from a particular point inside it known as its centre and the distance from centre to its boundary is known as the radius of the circle.
Quadrilateral: The area covered by four lines is known as a quadrilateral.
(i) Parallel lines: Parallel lines are the lines that never intersect to each other when extended either of the ends, the perpendicular distance between them is constant.
(ii)Perpendicular lines: If two lines intersect each other at 90° then these lines are called perpendicular lines.
(iii)Line segment: A line segment is a line of definite length,it has two end points.
(iv)Radius of the circle: The distance from the centre of the circle to any point that lies on the circle is known as the radius of the circle.
(v)Square:A quadrilateral whose all sides are equal and each of four angles are of 90°.
Purchase laptop of your own choice in Amazon
Q3. Consider the two postulates given below:
(i)Given any two distinct points A and B there exists a third point C, which is between A and B.
(ii)There exist at least three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent?
Do they follow from Euclid’s postulates? explain.
Ans.
Yes, here, the undefined terms are the ‘point’ and ‘line’
The (i) postulate says that there are two distinct points, A and B there exist a third point C, which is between A and B.
The (ii) postulate says that there exist at least three points that are not on the same line
Both of the postulates say different things,so postulates are consistent.
Euclid’s postulates are related to the following terms
Straight lines are drawn from one point to another point
Terminated line
Circle
Right angle
Two intersecting straight lines
Since both of these given postulates in the question don’t tell anything about the above-mentioned terms, so these postulates are not related to Euclid’s postulate.
Q4. If a pint C lies between two points A and B such that AC = BC, then prove that AC = 1/2AB. Explain by drawing the figure.
Ans.
We are given
AC = BC
Adding AC both sides
AC + AC = BC + AC
BC+AC = AB (BC+AC coincides with line segment AB)
2AC = AB (equals are added to equals then wholes are equal)
Q5. In question 4, point C is called the midpoint of line segment AB. Prove that every line segment has one and only midpoint.
Ans.
Let AB is the line segment and let instead of one mid point there are two mid points D and C of line segment AB.
Therefore
AC = BC ….(i) and AD = BD….(ii)
In equation (i) Adding AC both sides
AC + AC = BC + AC
BC + AC = AB (BC+AC and AB coincides to each other)
2AC = AB……(iii)
In equation (ii) Adding AD both sides
AD + AD = BD + AD
BD + AD= AB (BD +AD and AB both coincide to each other)
AD + AD = AB
2AD = AB…..(iv)
From (i) and (ii)
2AC = 2AD (If equals are equal to the same thing they are equal)
AC = AD (Things which are equal their double are also equal)
We conclude that C and D are the same points, it contradicts our assumption that C and D are two different midpoints of the line segments,so there can be only one mid point of a line segment.
Q6. In fig.5.10, if AC = BD, then prove that AB = CD.
Ans.
We are given
AC = BD
Subtracting BC from both sides
AC – BC = BD – BC
AB = CD( equals are subtracted from equal then reminders are equal)
Q7. Why is the axiom 5 in the list of Euclid’s axioms considered a ‘Universal truth’?(Note that question is not about the fifth postulate)
Ans. Euclid’s axiom 5 tells that whole is greater than the part of the whole. As an example, there is an apple, part of it like one-third of the apple is less than the whole apple, similarly, anything in the universe is always greater than the part of the whole thing, it’s that’s why axiom 5 is considered a ‘Universal Truth’.
Exercise 5.2
Q1. How would you rewrite Euclid’s fifth postulate so that it would be easier to understand?
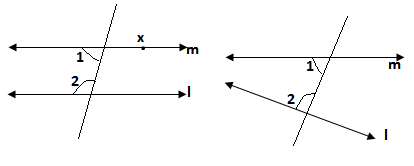
Ans.Euclid’s fifth postulate: If a straight and slant line is intersecting two straight lines forming two interior angles on the same side such that the sum of both angles is less than two right angles when two straight lines are produced indefinitely then both of them intersect on that side on which the sum of the angles is less than two right angles.
If both of the straight lines don’t intersect each other when produced indefinitely then both of the straight lines are parallel
In second figure ∠1 + ∠2 < 180° and in first figure ∠1 + ∠2 = 180°
So,we concluded from Euclid’s fifth postulate
- If x doesn’t lie on the line l then we can draw a parallel line through the point x
- There is a unique line m through x that is parallel to l
Q2.Does Euclid’s fifth postulate imply the existence of parallel lines? Explain.
Ans. Yes, Euclid’s fifth postulate implies the existence of the parallel lines. If the sum of the interior angles either side of the slant lines intersecting a pair of straight lines is equal to the sum of the right angles, then the two lines will not intersect each other at any point, hence both of them would be parallel to each other.
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions for class 9 maths
NCERT Solutions for class 9 science
NCERT Solutions for class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for Class 10 Science
NCERT Solutions for class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions for class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Class 12 Maths Important Questions-Application of Integrals
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution