NCERT Solutions Class 9 Exercise 7.4 of chapter 7-Triangles

NCERT Solutions of Class 9 Exercise 7.4 of chapter 7-Triangles are created here for helping the students of class 9 in helping their preparations for CBSE board exams. All NCERT Solutions of Class 9 Exercise 7.4 of chapter 7-Triangles are solved by an expert of maths in such a way that every student can understand easily without the help of anybody.

Click for online shopping

Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc

You can download the pdf of NCERT solutions of chapter 7

pdf of class 9 NCERT solutions of the chapter 7 -Triangle

Exercise 7.1- Triangles

Exercise 7.2- Triangle

Exercise 7.4 – Triangle

Q1.Show that in a right-angled triangle, the hypotenuse is the longest triangle.

Ans.

 

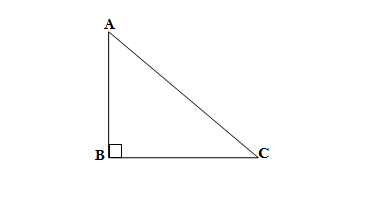
GIVEN: ΔABC is a right triangle,let ∠B =90°

TO PROVE: Hypotenuse is the largest side in a right triangle

PROOF: ∠B = 90°(given)

∠A + ∠B + ∠C  = 180° (angle sum property of the triangle)

∠A + 90° + ∠C  = 180°

∠A + ∠C  = 180°-90°= 90°

∠A and ∠C must be acute angle

∴∠A < 90° and ∠C < 90°

Therefore ∠B is the largest angle

So, ∠B >∠A  and ∠B>∠C

AC> BC and AC > AB (in a triangle side opposite to larger angle is longer)

Hence AC(hypotenuse)  is the largest side in a right triangle

Q2.In the given figure sides AB and AC of ΔABC are extended to points P and Q respectively .Also ∠PBC < ∠QCB. Show that AC > AB.

 

Ans.

GIVEN: In the fig. ∠PBC < ∠QCB

TO PROVE:AC > AB

PROOF: ∠PBC < ∠QCB(given)

∠ABC + ∠PBC = 180°(linear pair)

∠PBC = 180° – ∠ABC ….(i)

∠ACB + ∠QCB = 180°(linear pair)

∠QCB = 180° – ∠ACB ….(ii)

From equation (i) and equation (ii)

180° – ∠ABC < 180° – ∠ACB

∠ABC >∠ ACB

AC > AB (side opposite to larger angle is greater)

Q3.In the given figure , ∠B < ∠A, and ∠C < ∠D. Show that AD < BC.

 

Ans.

GIVEN: ∠B < ∠A, and ∠C < ∠D

TO PROVE:AD < BC

PROOF: ∠B < ∠A (given)

OA < OB….(i) (side opposite to larger angle is grater)

∠C < ∠D

OD < OC…(ii) (side opposite to larger angle is grater)

From equation (i) and equation (ii)

OA + OD < OB + OC

AD < BC (from figure), Hence proved

Q4.AB and CD are respectively smallest and the longest side of quadrilateral ABCD(see the given figure). Show that ∠A > ∠C and ∠B > ∠D.

 

Ans.

GIVEN: AB and CD are respectively smallest and the longest side of quadrilateral ABCD

COSTRUCTION: Joining A to C and B to D

TO PROVE: (i) ∠A > ∠C  (ii)  ∠B > ∠D.

(i) PROOF: In ΔABC

BC> AB (AB is the smallest side in ABCD)

∠BAC > ∠ACB ….(i) (side opposite to larger angle is grater)

In ΔADC

CD > AD (CD is the largest side in ABCD)

∠DAC > ∠ACD….(ii)

Adding equation (i) and (ii)

∠BAC + ∠DAC > ∠ACB + ∠ACD

∠A > ∠C, Hence proved

PROOF: (ii)  ∠B > ∠D

In ΔABD

AD> AB (AB is the smallest side in ABCD)

∠ABD > ∠ADB ….(i) (side opposite to larger angle is grater)

In ΔADC

CD > BC (CD is the largest side in ABCD)

∠DBC > ∠BDC….(ii)

Adding equation (i) and (ii)

∠ABD +∠DBC > ∠ADB + ∠BDC

∠B > ∠D, Hence proved

Q5.In the given figure , PR > PQ and PS bisects ∠QPR , prove that ∠PSR > PSQ.

 

Ans.

GIVEN:PR > PQ

PS bisects ∠QPR

∠QPS = ∠SPR

TO PROVE: ∠PSR >∠ PSQ

PROOF: PR > PQ (given)

∠Q > ∠R (side opposite to larger angle is grater)

In ΔPQS

∠Q + ∠QPS + ∠ PSQ = 180°(angle sum property of the triangle)

∠Q = 180° -(∠QPS + ∠ PSQ)…..(i)

In ΔPSR

∠R + ∠SPR + ∠ PSR = 180°(angle sum property of the triangle)

∠R = 180° -(∠SPR + ∠ PSR)…..(ii)

From (i) and (ii)

180° -(∠QPS + ∠ PSQ) > 180° -(∠SPR + ∠ PSR)

∠SPR + ∠ PSR >∠QPS + ∠ PSQ

Since PS bisects ∠P, ∠QPS = ∠SPR

∠SPR + ∠ PSR >∠SPR + ∠ PSQ

∠ PSR >∠ PSQ, Hence proved

Q6. Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.

Ans. Let A is an external point out of the line and AC⊥ BC

Let BC is a line and AB is a line segment drawn from the point A on the line BC

In triangle ΔABC

∠B <∠C (since ∠B is acute angle and ∠C =90°)

AC < AB (side opposite to larger angle is grater)

Similarly all line segments drawn from A on the line BC are larger than AC

Therefore AC is the shortest side drawn from A on BC, Hence proved

You can compensate us by donating any amount of money for our survival

Our Paytm NO 9891436286

You can compensate us

Paytm number 9891436286

The money collected by us will be used for the education of poor students who leaves their study because of a lack of money.

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions for class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions for class 9 science 

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

NCERT Solutions for class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT Solutions for Class 10 Science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

NCERT Solutions for class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT solutions for class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals

Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2

Class 12 Maths Important Questions-Application of Integrals

Class 12 Maths Important questions on Chapter 7 Integral with Solutions for term 2 CBSE Board 2021-22

Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22

Solutions of class 12  maths question paper 2021 preboard exam CBSE Solution