NCERT Solutions Class 9 Maths Exercise 8.1-Quadrilateral
NCERT Solutions Class 9 Maths Exercise 8.1 of chapter 8-Quadrilateral are based on the questions on different type of quadrilaterals like square,rectangle, rhombus and parallelogram. These NCERT solitions are the solutions of unsolved problems of class 9 maths NCERT text book exercise 8.1 of chapter 8-Quadrilaterals.All questions are solved by the subject expert.You can study here maths and science NCERT solutions, sample papers ,solutions of previous years question papers,important science and maths notes, articles on different type of competitice entrance exams and carrier in online jobs.
NCERT Solutions Class 9 Maths Exercise 8.1-Quadrilateral
Q1.The angles of quadrilateral are in the ratio 3 : 5 : 9: 13. Find all the angles of the quadrilateral.
Ans. Let the angles of quadrilateral are 3x, 5x, 9x and 13x
According to angle sum property of quadrilateral
3x + 5x + 9x + 13x = 360°
30x = 360°
x = 12
Therefore the required angles of quadrilateral are
3x = 3 × 12 = 36°
5x = 5× 12 = 60°
9x = 9 × 12 = 108°
13x = 13 × 12 = 156°
Q2.If diagonals of parallelogram are equal, then show that it is a rectangle.
Ans.
GIVEN: ABCD is a perallogram
Both diagonals are equal i.e BD =AC
TO PROVE: ABCD is a rectangle i.e ∠A= ∠B = ∠C = ∠D = 90°
PROOF: In ΔADC and ΔBDC
AD = BC (opposite sides of parallogram)
DC = DC (common)
BD = AC (given)
ΔADC ≅ BCD (SSS rule congruency of the triangles)
∠D = ∠C (by CPCT)
∠D + ∠C = 180° (Adjacent angles of parallogram)
∠D + ∠D = 180°
2 ∠D = 180°
∠D = 90°
Since we have proved ∠ D =∠C
∴∠C = 90°
∠A = ∠C (opposite angles of paralellogram)
∴∠A = 90°
∠B = ∠D (opposite angles of pallogram)
∴B = 90°
∠A = ∠B=∠C=∠D = 90°
Therefore ABCD is a rectangle, Hence proved
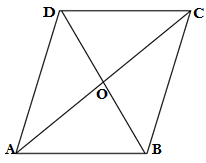
Q3. Show that diagonal of a quadrilateral bisect each other at right angles, then it is a rhombus.
Ans.
GIVEN: Diagonal of quadrilateral bisect each other
∴AO = CO and DO = BO
Diagonal of quadrilateral bisect each other at right angle
∠DOC = ∠AOD = ∠BOC = ∠AOB = 90°
TO PROVE:ABCD is a Rhombus
AB = BC = DC = AD
PROOF: In ΔAOD and ΔCOD
∠DOC = ∠AOD (given)
AO = CO (given)
DO = DO (common)
ΔAOD ≅ΔCOD (SSS rule congruency of Δ’s)
DC = AD (by CPCT)
Similarly we can prove
ΔAOD ≅ ΔAOB, ΔAOB ≅ ΔBOC, ΔBOC ≅ΔDOC
So,AD = AB, AB = BC,BC =DC (by the rule of CPCT)
Therefore ABCD is a rhombus
Hence proved
Q4. Show that diagonals of a square are equal and bisect each other at right angle.
Ans.
GIVEN: ABCD is a square
TO PROVE: AC = BD
AC and BD bisect each other at right angle i.e ∠DOC = ∠DOA = ∠AOB = ∠BOC = 90°
PROOF: In ΔABD and ΔABC
AB = AB (common)
AD = BC (sides of square)
∠A = ∠B = 90° (angles of square)
ΔABD ≅ ΔABC (SSS rule of congruency)
AC = BD (by CPCT)
Hence diaogonals of square are equal
In ΔAOD and ΔBOC
∠AOD = ∠BOC (vertically opposite angles)
∠DAO = ∠BCO (alternate angles)
AD = BC (sides of square)
ΔAOD ≅ ΔCOB ( AAS rule)
AO = CO ( by CPCT)
DO = BO (by CPCT)
Hence diagonals of square bisect each other
Now, considering the ΔDOC and ΔDOA
AD = DC (sides of square)
DO = DO (common)
AO = CO ( proved above )
ΔDOC ≅ΔDOA (SSS rule)
∠DOC =∠DOA (by CPCT)
∠DOC +∠DOA = 180°
∠DOC +∠DOC= 180°
2∠DOC = 180°
∠DOC = 90°
∠DOA = 90°
∠BOC = ∠DOA = 90° (vertically opposite angle)
∠DOC = ∠AOB = 90°(vertically opposite angle)
∠DOC = ∠DOA = ∠AOB = ∠BOC = 90°
Hence diagonal of square bisect each other at 90°
Q5. Show that diagonal of a quadrilateral are equal and bisect each other at right angle,then it is a square.
Ans.
GIVEN:AC = BD
∠DOC = ∠DOA = ∠AOB = ∠BOC = 90°
AO = CO
DO = BO
TO PROVE:ABCD is a sqare
PROOF:In ΔAOD and ΔCOD
DO = DO (common)
AO = CO (given)
∠DOA = ∠COD = 90°(given)
ΔAOD ≅ΔCOD (SAS rule)
AD = DC (by CPCT )
Similarly, ΔAOD ≅ΔAOB
AD = AB (by CPCT)
and ΔAOB≅ΔCOB
AB = BC
∴AB = BC= AD=DC
Therefore all sides of quadrilateral are equal
Now, we have to prove all angles of quadrilateral are of 90°
In ΔABC and ΔABD
AD =BC (proved above)
AB = AB (common)
BD = AC (given)
ΔABC≅ΔBAC
∠A = ∠B (by CPCT)
Since we have proved all sides are equal so ABCD is a parallogram and ∠A , ∠B are adjacent angles.
∴∠A + ∠B = 180°
Putting ∠A = ∠B
∠B + ∠B = 180°
2∠B= 180°⇒ ∠B = 90°and ∠A = 90°
∠A = ∠C = 90°, ∠B = ∠D =90° (opposite angles of parallogram)
Each angle of the given quadrilateral are of 90°
In given quadrilateral all sides are equal and each of four angles are of 90°
Hence ABCD is square.
Latest electronic items,mobiles,laptops and desktops at easy instalments
NCERT Solutions Class 9 Maths Exercise 8.1-Quadrilateral
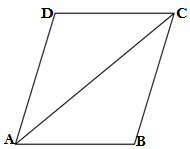
Q6. Diagonal AC of a parallelogram ABCD bisects ∠A (see the given figure). Show that
(i) It bisects ∠C also
(ii)ABCD is a rhombus
Ans.
GIVEN: ABCD is a parallelogram
in which diagonal AC bisects ∠A
TO PROVE:Diagonal AC bisects ∠C
ABCD is a rhombus i.e AB = BC = CD = AD
PROOF :In ΔADC and ΔABC
∠DAC = ∠CAB…..(i) (given)
∠DAC = ∠ACB…..(ii) (alternate angle )
∠ACD = ∠CAB…..(iii)(alternate angle )
From equation (i) and equation (ii)
∠DAC = ∠ACB….(iv)
From (i) and (iii)
∠DAC = ∠ACD ….(v)
From equation (iv) and (v)
∠ACD = ∠ACB
Therefore AC bisects ∠C also
Now, we have to prove ABCD is rhombus
∠A = ∠C (opposite angles of parallogram)
∠A /2= ∠C/2
∠DAC = ∠ACD (AC bisects ∠A is given AC bisects ∠C, proved above)
DC = AD (opposite sides of equal engle in a triangle)
DC = AB (opposite sides of parallelogram)
AD =BC (opposite sides of parallelogram)
∴DC = AD =AB = BC
Hence ABCD is a rhombus
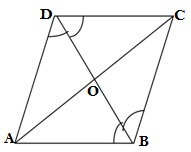
Q7. ABCD is a rhombus . Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.
Ans.
GIVEN: ABCD is a rhombus
TO PROVE: ∠ODA= ∠CDO, ∠OBC = ∠OBA
∠DCO = ∠BCO, ∠OAB = ∠DAO
PROOF: In ΔADB
AD = AB (sides of rhombus)
∠ADO = ∠OBA ….(i)(opposite angles of equal sides)
∠ADO = ∠OBC …..(ii)(alternative angle)
From equation (i) and equation (ii)
∠OBA =∠OBC …..(iii)
In ΔBDC
DC = BC (sides of rhombus)
∠OBC=∠CDO…..(iv)(opposite angles of equal sides)
∠OBC = ∠ODA….(v)(alternative angle)
From equation (iv) and equation (v)
∠CDO = ∠ODA…..(vi)
Equation (iii) and equation (vi) shows that BD bisects ∠B as well as ∠D
Similarly we can prove that AC bisects ∠A as well as ∠C
Q8.ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that
(i) ABCD is a square
(ii) Diagonal BD bisects ∠B as well as ∠D
Ans.
GIVEN: ABCD is a rectangle
∠DAC = ∠BAC
∠DCA = ∠BCA
TO PROVE :
(i) ABCD is a square
(ii) Diagonal BD bisects ∠B as well as ∠D
∠ADB=∠BDC, ∠ADB = ∠DBC
PROOF: In ΔBCA
∠DAC = ∠BAC (given)
∠DCA = ∠BCA (given)
∠A = ∠C = 90° (angles of rectangle)
∠DAC = ∠BAC = ∠A/2 = 90°/2 = 45°
∠DCA = ∠BCA = ∠C/2 = 90°/2 = 45°
∠BAC = ∠BCA
AB = BC
∠DAC = ∠DCA
AD = DC (opposite sides of equal angles in a triangle)
Therefore AB = DC, BC = AD (opposite sides of rectangle)
⇒ AB = BC = DC = AD
Hence ABCD is a square
We have to prove (ii) Diagonal BD bisects ∠B as well as ∠D
TO PROVE: Diagonal BD bisects ∠B as well as ∠D
PROOF: In ΔAOD and ΔCOD
BC = AB(proved above)
DO = DO (common)
AO = CO (diagonal of rectangle bisect each other)
ΔAOD ≅ COD (SSS rule)
∠ADO =∠CDO (by CPCT)…..(i)
In ΔAOB and ΔCOB
AD = DC (proved above)
BO = BO (common)
AO = CO (diagonal of rectangle bisect each other)
ΔAOB≅ COB (SSS rule)
∠OBA=∠OBC (by CPCT)……(ii)
Equation (i) and equation (ii) shows that BD bisects ∠B as well as ∠D, Hence proved.
NCERT Solutions Class 9 Maths Exercise 8.1-Quadrilateral
Q9. In parallelogram ABCD, two points P ad Q are taken on diagonal BD such that DP = BQ(see the given figure). Show that
(i) ΔAPD ≅ ΔCQB
(ii) AP = CQ
(iii) ΔAQB ≅ ΔCPD
(iv) AQ = CP
Ans.
GIVEN: ABCD is a parallelogram
P and Q are the points on diagonal BD
DP = BQ
TO PROVE:
(i) ΔAPD ≅ ΔCQB
(ii) AP = CQ
(iii) ΔAQB ≅ ΔCPD
(iv) AQ = CP
PROOF: (i) In ΔAPD and ΔCQB
AD = BC (opposite sides of parallelogram)
DP = BQ (given)
∠ADP = ∠CBQ (alterative angle)
ΔAPD ≅ ΔCQB (SAS rule)
PROOF: (ii) AP = CQ
Since,we have already proved above in (i)
ΔAPD ≅ ΔCQB
Therefore AP = CQ (by CPCT)
PROOF: (iii) ΔAQB ≅ ΔCPD
In ΔAQB and ΔCPD
AB = CD (opposite sides of parallelogram)
DP = BQ (given)
∠ABQ = ∠CDP (alterative angles)
ΔAQB ≅ ΔCPD( SAS rule)
PROOF:(iv) AQ = CP
ΔAQB ≅ ΔCPD(proved above)
AQ = CP (by CPCT)
You can compensate us
Paytm number 9891436286
The money collected by us will be used for the education of poor students who leaves their study because of a lack of money.
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions for class 9 maths
NCERT Solutions for class 9 science
NCERT Solutions for class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for Class 10 Science
NCERT Solutions for class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions for class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Class 12 Maths Important Questions-Application of Integrals
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution