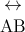Lines, angles, and triangles
Lines, angles and triangles are the basics of all the questions based on geometry which is a part of the maths textbook from class 6, class 7, class 8, class 9 and class 10. Before we study Lines, Angles and Triangles let’s know geometry concepts.
Geometry is gotten from two Latin words, geo +metron means the importance of earth and estimation. In this way, it is the study of the properties and relations of points, lines, surfaces, solids, and higher dimensional analogues.
Why we Study about Geometry?
To discover Length, Area, Volume of various Plane and Solid figures of utilization which are available around us in this world and to think better about them.
Contemporary geometry has numerous subfields which are as per the following-
(I) Algebraic Geometry – It is a part of geometry concentrating zeros of a multivariate polynomial. It incorporates direct and polynomial mathematical condition utilized for understanding about the arrangements of zeros. The use of this sort incorporates Cryptography, string hypothesis and so on.
(ii) Discrete Geometry – It is concerning about the relative position of straight forward geometric articles, for example, points, lines, triangles, circles and so on.
(iii) Differential Geometry – It utilizes procedures of algebra and calculus for the solution of critical problems. The different issue incorporate general relativity in material science and so on.
(iv) Euclidean Geometry – The investigation of the plane and strong figures based on axioms and postulates including points, lines, planes, angles, congruence, similarity, solid figures. It has a wide scope of use in Computer Science, Modern Mathematics critical thinking, Crystallography and so on.
(v) Convex Geometry –It incorporates curved shapes in Euclidean space utilizing methods of genuine analysis. It has application in optimization and functional analysis in number hypothesis.
Another method for classification of Geometry incorporates Plane and Solid Geometry.
Plane Geometry – This wing of Geometry manages level shapes which can be drawn on bit of paper. These include lines, circles, and triangles of two measurements.
Solid Geometry – It manages 3-dimensional articles like 3D shapes, crystals, chambers and circles.
What are Surds and how to compare them?
How to select subjects after 10 and 12 Pass ?
Techniques of Achieving Hundred Percent Marks in Mathematics.
Tips to get success in competitive exams
Finding the roots of the polynomial by the complete square method
Addition, subtraction, multiplication and division of polynomials
Number System(all types of numbers used in maths)
How to creat linear equations in one and two variable
Point-
Point is used for showing the endpoint of a line and location of a point, it is dimensionless. It is represented by the symbol •.
Line-
Line has length but no width at all, it has no endpoints and can be extended towards both ends, the points are used here just for showing the name of the line..It is represented by the symbol ↔.The given line in the figure is expressed as
Ray-
Ray has one endpoint and can be extended towards its direction. It is represented by the symbol →, the given ray in the figure is expressed as
Line segment-
The line of definite length is known as the line segment, it is represented by the symbol —.The line segment in the given figure is expressed as
Parallel lines-
The parallel lines are the pairs of lines which never intersect each other if extended further and when a transversal is allowed to pass through them their corresponding and alternative angels are always equal.
Corresponding Angles-
The pair of angles formed on the same side of the transversal line and the parallel lines are known as corresponding angles, as in the above figure (∠1, ∠5), (∠2, ∠6) (∠4, ∠8), (∠3, ∠7)are corresponding angles.
Corresponding angles formed by a transversal and two parallel lines are always equal
∠1= ∠5, ∠2 = ∠6, ∠4= ∠8, ∠3= ∠7
Alternative Angles-
The pair of angles formed by the transversal line and the parallel lines in the opposite side of both of them are known as alternative angles, as an example, in the figure, the pair of alternatives angles are (∠1, ∠7), (∠2, ∠8), (∠4,∠6), (∠3, ∠5)
Alternative angles formed by a transversal and two parallel lines are always equal
∠1= ∠7, ∠2 = ∠8, ∠4= ∠6, ∠3= ∠5
Click-For online purchasing of Computer and Accessories
Co-interior Angles –
The pair of interior angles formed by the parallel lines and the transversal lines in the same side of the transversal line is called co-interior angles, example: (∠4, ∠5), (∠3,∠6). The sum of co-interior angles is equal to 180º,∠4 +∠5 = 180º,∠3+∠6 = 180°
Triangle-
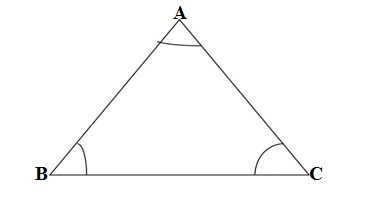
Triangle is a polygon of three sides which has three angels and three vertexes.
In the above fig. ΔABC has the following parts.
Sides-
AB, BC and AC
Angles-
∠A, ∠B and ∠C
Vertexes-
A, B and C
Properties of the triangle-
1-The sum of three interior angles of the triangle is 180º which is called the angle sum property of the triangle.
∠A + ∠B + ∠C = 180° where ∠A,∠B and ∠C are the interior angles of the ΔABC.
2-The sum of two sides of Δ is always greater than another side.
AB + BC > AC
BC + AC > AB
AB+ AC > BC
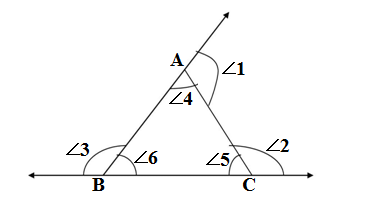
3- The exterior angle of Δ is equal to the sum of interior angles located at the opposite vertexes.
In the fig. the relationship of exterior angles with the angles on opposite sides is as follows.
∠1 = ∠6 + ∠5
∠2 = ∠4 + ∠6
∠3 = ∠4 + ∠5
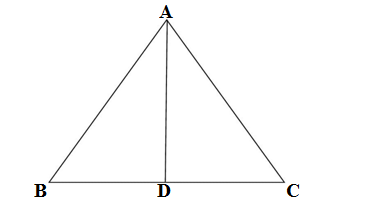
Ex. In the following fig. of triangle ABC.
Prove that AB > 2(AD- BD)
AB + BD >AD
AC + DC > AD
AB+2BD >2AD
AB > 2(AD- BD)
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
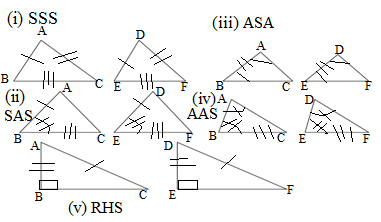
Congruency of triangles-
The triangles are called congruent if their corresponding sides are equal.
Criteria of congruent triangles-
SSS rule-
BD = DE, BC = EF, AC = DF
ΔABC ≅DEF
SAS rule-
AB = DE, BC = EF, AC = DF
ΔABC ≅DEF
ASA rule-
AB = DE, BC = EF, AC = DF
ΔABC ≅DEF
AAS rule-
AB = DE, BC = EF, AC = DF
ΔABC ≅DEF
RHS rule –
AB = EF, AC = DF, ∠B = ∠E = 90°.
ΔABC ≅DEF
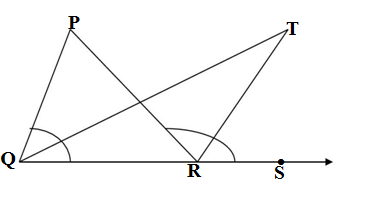
Example of question-based on the properties of the triangle-
In fig., the side QR of ∆ QPR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that
Solution-
In ∆ QPR using the relation between exterior and interior angles .
∠PRS = ∠PQR + ∠QPR………(1)
Using the same relation in ∆QTR
∠TRS = ∠TQR + ∠QTR
<PRS = <PQR + 2<QTR…….(2)
From (1) and (2)
<PQR + <QPR = <PQR + 2<QTR
∠QPR = 2<QTR
Hence Proved
Study the Questions Based on the Following Geometrical figgures
Questions Based on Areas of Parallelogram and Triangles