NCERT Solutions Class 9 Maths Exercise 9.1 and 9.2 -Areas of Parallelogram and Triangles

NCERT Solutions Class 9 Maths Exercise 9.1 and 9.2 of Chapter 9-Areas of Parallelogram and Triangle is very important to study for the exam preparations. These NCERT solutions are the solutions of unsolved questions of class 9 NCERT maths textbook exercise 9.1 and 9.2 of chapter 9 .All questions are solved by the expert by a step by step method.

Here you can study science and maths from class 9 to 12, our articles on competitive entrance exams, carrier in online jobs. You can also download e-books of maths, science, physics, chemistry, biology, and e-books on the carrier.

Click for online shopping

Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc

NCERT Solutions class 9 maths of chapter 9-Areas of parallelogram and triangles

Exercise 9.3-Areas of Parallelogram and Triangles

Download pdf of NCERT solutions of class 9 maths chapter 9-Areas of Parallelogram and Triangle

PDF-NCERT solutions of class 9 maths chapter 9-Areas of Parallelogram

NCERT Solutions of Class 9 Science : Chapter 1 to Chapter 15

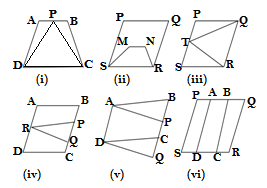
Q1. Which of the following figure lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.

 

Ans.

(i) In figure (i) parallelogram ABCD and ΔPCD are  between the same parallels,the common base is DC and the two parallel lines are AB ∥ DC.

(ii)In figure (ii) parallelogram PQRS and quadrilateral MNRS are not between the same parallels, although the common base is SR

(iii) In figure (iii) quadrilateral PQRS and ΔQTR are between the same parallels,the common base is QR and the two parallel lines are PS ∥ QR.

(iv) In figure (iv) parallelogram ABCD and ΔPBQ are not between the same parallels AD∥BC, but there is no common base.

(v) In figure (v) quadrilateral ABQD and quadrilateral APCD are  between the same parallels AD∥ BQ and the common base is AD.

(vi) In figure (vi) quadrilateral PQRS and quadrilateral ABCD are between the same parallels PQ∥ SR but they don’t have a common base.

Exercise 9.2

Q1. In the given figure ABCD is a parallelogram ,AE ⊥ DC and CF ⊥ AD.If  AB = 16 cm,AE = 8 cm and CF = 10 cm,find AD.

 

Ans. Area of parallelogram = 1/2 (Base × altitude)

AB = DC= 16 cm (opposite sides of parallelogram)

Area of parallelogram ABCD = 1/2(DC × AE) =1/2(16×8) =64 cm²

Area of parallelogram ABCD = 1/2(AD × CF) =1/2(AD×10)

1/2(AD×10)  = 64

10 AD = 128
AD = 12.8 cm

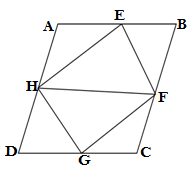
Q2.If E, F,G and H are respectively are the mid points of the sides of a parallelogram ABCD ,show that

Ans.

GIVEN: ABCD is a parallelogram

E, F, G, and H are midpoints of AB, BC, CD, and AD respectively

CONSTRUCTION: Joining the points H and F

TO PROVE:

PROOF: H and F are the mid points of AD and BC respectively

∴HF ∥ DC and HF =DC

HFCD will be a parallelogram

Since the area of a triangle is half of the area of a parallelogram between the same parallels and on the common base.

H and F are the midpoints of AD and BC respectively

∴HF ∥ AB and HF =AB

ABFH will be a parallelogram

Adding both equations (i) and (ii)

Hence proved

Q3. P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD.Show that ar(APB) = ar(BQC).

Ans.

GIVEN: ABCD is a parallelogram

P and Q are the points on the sides DC and AD respectively

TO PROVE: ar(APB) = ar(BQC).

PROOF: The area of a triangle is half of the area of a parallelogram between the same parallels and on the common base

Here parallelogram ABCD and ΔAPB are on the same base AB and between the same parallels AB ∥ DC.

Parallelogram ABCD and ΔBCQ are on the same base AB and between the same parallels AD ∥ BC

From equation (i) and equation (ii)

ar(APB) = ar(BQC), Hence proved

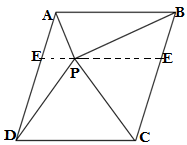
Q4. In the given figure,P is a point in the interior of a parallelogram ABCD. Show that 

(i) ar(APB) + ar(PCD) = 1/2 ar(ABCD)

(ii) ar(APD) + ar(PBC)= ar(APB) + ar(PCD)

(Hint: Through P draw a line parallel to AB)

Ans.

GIVEN:P is a point in the interior of a parallelogram ABCD

CONSTRUCTION: Drawing a line FE through P such that FE∥AB∥ DC.

TO PROVE:

(i) ar(APB) + ar(PCD) = 1/2 ar(ABCD)

(ii) ar(APD) + ar(PBC)= ar(APB) + ar(PCD)

PROOF:

(i) AB ∥ FE (constructed)

AF∥BE (since AD ∥ BC)

ABEF will be a parallelogram

ΔAPB and ABEF are the triangle and parallelogram on the same base AB and between the same parallels AB ∥ FE.

ΔPCD and FECD are the triangle and parallelogram on the same base DC and between the same parallels DC ∥ FE

Adding both equation (i) and (ii)

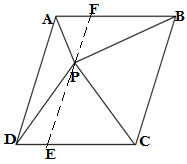
(ii)

Drawing a line EF such that EF∥AD∥BC

AFED and ΔAPD are the parallelogram and triangle on the same base AD and between the same parallels AD ∥ FE

FBCE and ΔPBC are the parallelogram and triangle on the same base BC and between the same parallels BC ∥ FE

Adding both equation (i) and (ii)

Since, we already have proved in (i)

Therefore

ar(APD) + ar(PBC)= ar(APB) + ar(PCD),Hence proved

Q5.In the given figure ,PQRS and ABRS are parallelograms and X is any point on side BR .Show that

(i) ar(PQRS) = ar(ABRS)

(ii) ar(AXS) = 1/2 ar( PQRS)

Ans.(i) Parallelograms PQRS and ABRS are on the same base SR and between the same parallels PB ∥ SR

∴ ar(PQRS) = ar(ABRS)

(ii) Tringle AXS and Parallelogram ABRS are on the same base AS and between the same parallels AS∥ BR.

ar(AXS) = 1/2 ar(ABRS)…..(i)

ar(PQRS) = ar(ABRS)[proved above]…….(ii)

From equation (i) and (ii)

ar(AXS) = 1/2 ar(PQRS), Hence proved

Q6.A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts the field is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?

Ans.

 

Ans. PQRS is a field in the form of a parallelogram

A is a point on RS that is joined to P and Q

The field is divided into three triangular parts ΔPAS, ΔPQA and ΔQAR

ar(ΔPAS) +ar(ΔPQA) + ar(ΔQAR) = ar(PQRS)

PQRS and ΔPQA are the parallelogram and triangle on the same base PQ and between the same parallels PQ ∥ SR

ar(ΔPQA) = 1/2 ar(PQRS)….(i)

ar(ΔPAS) + ar(ΔQAR)= 1/2 ar(PQRS)

ar(ΔPAS )+ ar(ΔQAR)+ 1/2 ar(PQRS)= ar(PQRS)

ar(ΔPAS) + ar(ΔQAR) = ar(PQRS) – 1/2 ar(PQRS)

ar(ΔPAS) + ar(ΔQAR) =  1/2 ar(PQRS)….(ii)

From equation (i) and (ii)

ar(ΔPAS) + ar(ΔQAR) = ar(ΔPQA)

The relationship between the triangular parts ΔPAS ,ΔPQA and ΔQAR shows that the farmer will sow wheat in ΔPQA and pulses in ΔQAR and ΔPAS or its vise versa.

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions for class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions for class 9 science 

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

NCERT Solutions for class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT Solutions for Class 10 Science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

NCERT Solutions for class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT solutions for class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals

Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2

Class 12 Maths Important Questions-Application of Integrals

Class 12 Maths Important questions on Chapter 7 Integral with Solutions for term 2 CBSE Board 2021-22

Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22

Solutions of class 12  maths question paper 2021 preboard exam CBSE Solution