Class 9 Maths Chapter 13 Exercise 13.7 - Surface Areas and Volumes NCERT Solutions

Class 9 Maths Chapter 13 Exercise 13.7 - Surface Areas and Volumes NCERT Solutions with PDF
NCERT Solutions for Class 9 Maths Exercise 13.7 from Chapter 13 Surface Areas and Volumes are provided here to help students prepare for their Term 2 CBSE Board exams. All the questions in Class 9 Maths Chapter 13 Exercise 13.7 are solved by an experienced CBSE Maths instructor.
Exercise 13.7 focuses on the surface areas and volumes of three-dimensional conical shapes that we encounter in daily life. These solutions are valuable not only for your CBSE exams but also for competitive entrance exams.
The NCERT Solutions for Class 9 Maths Chapter 13 are essential study materials for the CBSE Board exam preparation, as Chapter 13 – Surface Areas and Volumes covers a variety of real-life problem-solving questions.
Download Class 9 Maths Chapter 13 Exercise 13.7 NCERT Solutions PDF
Download the Class 9 Maths Chapter 13 Exercise 13.7 NCERT Solutions PDF for Surface Areas and Volumes. This essential guide includes all the Class 9 Maths Chapter 13 Solutions, making it easier for you to complete your homework and prepare for exams effectively. The PDF format allows you to study offline, so you can access the Class 9 Chapter 13 Maths Solutions anytime, anywhere.
Class 9 Maths Chapter 13 - Surface Areas and Volumes: Find Links to All Exercises NCERT Solutions
Class 9 Maths Chapter 13 Exercise 13.7 - Surface Areas and Volumes NCERT Solutions
Q1. Find the volume of the right circular cone with
(i) radius 6cm, height 7 cm
(ii) radius 3.5 cm, height 12 cm (Assume π = 22/7)
Solution.
(i) Radius(r) of the right circular cone is 6 cm and height(h) is 7 cm
Volume of the right circular cone
=(1/3) πr²h
=(1/3)×(22/7)×6×6×7
=22×2×6
=264
Hence the volume of the cone is 264 cm³
(ii) Radius(r) of the right circular cone is 3.5 cm and height(h) is 12 cm
Volume of the right circular cone
=(1/3) πr²h
=(1/3)×(22/7)×3.5×3.5×12
=22×0.5×3.5×4
=154
Hence the volume of the cone is 154 cm³
Q2.Find the capacity in liters of a conical vessel with
(i) radius 7cm, slant height 25 cm (ii) height 12 cm, slant height 13 cm (Assume π = 22/7)
Solution. (i) Radius (r) of the conical vessel is 7cm, slant height (l) is 25 cm
height(h) =√(l²-r²) = √(25²-7²) =√(625-49) =√576=24 cm
The capacity of the conical vessel is
=(1/3)πr²h
=(1/3)×(22/7)×7×7×24
=22×7×8
=1232
The volume of the vessel is 1232 cm³
Hence the capacity of the conical vessel is 1232 cm³=[1232 ÷1000]litres=1.232 l
(ii) Height (h) of the conical vessel is 12cm, slant height(l) is 13 cm
Radius(r) =√(l²-h²) = √(13²-12²) =√(169-144) =√25=5 cm
The volume of the conical vessel is
=(1/3)πr²h
=(1/3)×(22/7)×5×5×12
=(22/7)×5×5×4
=2200/7
The volume of vessel is 2200/7 cm³
Hence the capacity of the conical vessel is 2200/7 cm³=[2200/7 ÷1000] litres=11/35 l
Q3. The height of a cone is 15cm. If its volume is 1570cm3, find the diameter of its base. (Use π = 3.14)
Solution. The height(h) of a cone is 15cm
Volume of the cone is
=πr²h
=(22/7)×r²×15
Volume of the cone is given 1570cm³1570×21)/(22×15)
∴(1/3)(22/7)×r²×15 = 1570
(1/3)(3.14)×r²×15 = 1570
3.14 ×r²×5= 1570
r² = (1570)/(3.14×5)
r² = 1570/15.7 =100
r = √100 =10
Hence the diameter of base of the cone is 2r =2×10 =20 cm
Q4. If the volume of a right circular cone of height 9cm is 48πcm3, find the diameter of its base.
Solution. Height (h)of the right circular cone is 9 cm
Volume of the right circular cone is given 48πcm³
Volume of the right circular cone = πr²h
(1/3)πr²h = 48π
(1/3)πr²×9 = 48π
r² = (48×3)/9=16
r = √16 =4
Hence the diameter of the base of right circular cone is 2r =2×4 =8 cm
Class 9 Maths Chapter 13 Exercise 13.7 - Surface Areas and Volumes NCERT Solutions
Q5.A conical pit of top diameter 3.5m is 12m deep. What is its capacity in kiloliters? (Assume π = 22/7)
Solution. The diameter of the top of the conical pit is 3.5 m,then its radius is 3.5/2 =1.75 m
The depth(h) of the pit is 12 m
The volume of the pit
=(1/3)πr²h
=(1/3)(22/7)×1.75×1.75×12
=22×0.25×1.75×4
=38.5
The volume of pit is 38.5 m³
1 Kl = 1m³
Hence the capacity of the pit is 38.5 ×1 =38.5 Kilo liters
Q6. The volume of a right circular cone is 9856cm³. If the diameter of the base is 28cm, find
(i) height of the cone
(ii) slant height of the cone
(iii) curved surface area of the cone
(Assume π = 22/7)
Solution. The diameter of the base of a right circular cone is 28 cm then its radius(r) is 14 cm
The volume of a right circular cone is
=(1/3)πr²h
The given volume of the right circular cone is 9856cm³
(1/3)×(22/7)×14×14h = 9856
(1/3) ×22×2×14h = 9856
h = ( 9856×3)/(44×14)
h=48
Hence the height of the cone is 48 cm
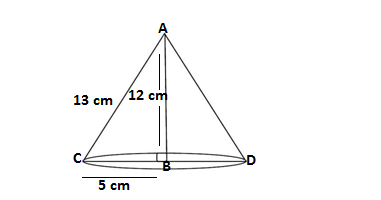
Q7. A right triangle ABC with sides 5cm, 12cm and 13cm is revolved about the side 12 cm. Find the volume of the solid so obtained.
Solution. Since right Δ ABC is is revolved about the side 12 cm,therefore the height(h) of so formed cone is 12 cm and radius(r) is 5 cm and slant height(l) is 13 cm
Volume of the so formed cone =(1/3)πr²h
Where r =5 cm,h =12 cm
Volume
= (1/3)π×5×5×12
=100π
Hence the volume of the so formed cone is 100π cm³
Q8.If the triangle ABC in the Question 7 is revolved about the side 5cm, then find the volume of the solids so obtained. Find also the ratio of the volumes of the two solids obtained in Questions 7 and 8.
Solution. Since right Δ ABC is is revolved about the side 5 cm,therefore the height(h) of so formed cone is 5 cm and radius(r) is 12 cm and slant height(l) is 13 cm
Volume of the so formed cone =(1/3)πr²h
Where r =12 cm,h =5 cm
Volume
= (1/3)π×12×12×5
=240π
Hence the volume of the so formed cone is 240π cm³
Ratio of the volumes of the two solids obtained in Questions 7 and 8
100π : 240π
=5 : 12
Hence the ratio of the volumes of the two solids is 5 : 12
Q9. A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas.
Solution. The diameter of conical heap is 10.5 m therefore its radius(r) is 10.5/2 =5.25 m and height(h) is 3 m
The volume of the heap
=(1/3)πr²h
=(1/3)×(22/7)×5.25 ×5.25 ×3
=22×0.75 ×5.25
=86.625
The volume of the heap is 86.625 m³
The heap is to be covered by canvas to protect it from rain
= Curved surface area of the heap
= πrl,where r =5.25 m
Slant height(l) =√(h²+r²) =√(3²+5.25²)=√(9+27.5625)=√(36.5625)=6.05 m
Curved surface area of the heap
=(22/7)×5.25×6.05
=22×0.75×6.05
=99.825
Hence the canvas required to covered the heap is 99.825 m²
Conclusion - Class 9 Maths Chapter 13 Exercise 13.7 - Surface Areas and Volumes
Understanding Class 9 Maths Chapter 13 Exercise 13.7 is important for getting the hang of Surface Areas and Volumes. Our simple, step-by-step solutions for Class 9 Maths Chapter 13 Exercise 13.7 will help you work through each problem easily. With these solutions, Surface Areas and Volumes will feel much easier to learn. Be sure to download the PDF for Class 9 Chapter 13 Maths Exercise 13.7, so you can practice anytime and keep these key concepts handy. Keep practicing, and you’ll do great in your exams!
You Can Also Study
NCERT Solutions of class 9 maths
| Chapter 1- Number System | Chapter 9-Areas of parallelogram and triangles |
| Chapter 2-Polynomial | Chapter 10-Circles |
| Chapter 3- Coordinate Geometry | Chapter 11-Construction |
| Chapter 4- Linear equations in two variables | Chapter 12-Heron’s Formula |
| Chapter 5- Introduction to Euclid’s Geometry | Chapter 13-Surface Areas and Volumes |
| Chapter 6-Lines and Angles | Chapter 14-Statistics |
| Chapter 7-Triangles | Chapter 15-Probability |
| Chapter 8- Quadrilateral |