Class 10 Maths Question Paper CBSE Half Yearly Exam 2022 With Solutions

Class 10 Maths Question Paper CBSE Half Yearly Exam 2022 With Solutions is published here to assist class 10 students in boosting their preparation of CBSE board exams.The question paper contains three section A,B and C.Section  A has part l and part ll which contains 4 case study questions and Section C is divided into part part lll.part iv and part v.Section A contains 15 questions each of 1 mark, section B has 4 case study questions,case study 1 contains 2 questions each of 2 marks, case study 2,3 and 4 contains 5 questions and you have to solve only 4 questions out of 5 in each case study which are of 1 marks each.Section C is divided into three parts,part lll contains 6 questions each of 2 marks,part iv contains 7 questions each of 3 marks and part v contains 3 questions each of 4 marks.Internal choice of one question is given in part iv and part v.

Class 10 Maths Question Paper CBSE Half Yearly Exam 2022 With Solutions

General Instruction:
All questions are compulsory

Section A

(Part l)

Q1.If sin²θ = 1/(1 +tan²θ) then θ =

Solution:

The given equation is

sin²θ = 1/(1 +tan²θ)

sin²θ = 1/sec²θ

sin²θ = cos²θ

sin²θ = 1- sin²θ

2sin²θ -1 = 0

sin²θ -1/2 =0

sin²θ -(1/√2)² =0

(sinθ +1/√2)( sinθ – 1/√2) = 0

sinθ  = -1/√2, sinθ = 1/√2

sinθ = sin45°

θ =45°

Q2.If cotθ = 7/8 then find the value of (1 +cosθ)(1 -cosθ)/(1 -sinθ)(1 +sinθ)

Solution:

Given that cotθ = 7/8

(1 +cosθ)(1 -cosθ)/(1 -sinθ)(1 +sinθ)

=(1- cos²θ)/(1-sin²θ)

=sin²θ/cos²θ

=tan²θ

= 1/cot²θ = (8/7)² = 64/49 Since cotθ = 7/8

Q3.If cosecθ = 5/3 then find the value  of cosθ +tanθ

Solution:

It is given that cosecθ = 5/3

Since cosecθ = hypotenuse(h)/perpendicular(p)

Base(b) = √(h²-p²) = √(5²-3²) =√(25-9) =√16 =4

cosθ +tanθ  = b/h + p/b = 4/5 +3/4 =(16+15)/20 = 31/20

Q4.If sinθ = 4/5 then cosθ = ?

Solution:

It is given that sinθ = 4/5

Since sinθ = perpendicular(p)/hypotenuse(h)

Base(b) = √(h²-p²) = √(5²-4²) =√(25-16) =√9 =3

cosθ = b/h = 3/5

See the video: Solution of Class 10 Maths Solution ,Preboard Question paper 2021-22 CBSE board

Q5.Value of cos0°.cos30°.cos45°.cos60°.cos90° is…….

Solution:

cos0°.cos30°.cos45°.cos60°.cos90°

Since the value of cos90°= 0

Therefore

(cos0°.cos30°.cos45°.cos60°)× 0=0

Q6.(i) If P(E) =0.08 find P(E’) =

Solution:

P(E) =0.08,

We have

P(E) + P(E’) = 1

P(E’) = 1 – P(E)  = 1 -0.08 = 0.92

(ii) A card is selected from a deck of 52 cards. The probability of its being a red face card is………

Solution: Total number of cards = 52

Total number of red face cards = 26

P(red face cards) = Total number of red face cards /Total number of cards

P(red face cards) = 26/52 = 1/2

Q7.Median of 35,38,39,34,35,37,38,40,42,45,41,41,40,35,37,38,36,40,36,37

Solution:

Arranging the given number in ascending order

34,35,35,35,36,36,37,37,37,38,38,38,39,40,40,40,41,41,42,45

No. of observations are = 20

20(n) is even no. therefore applying the following median formula

Median = [(n/2) th term + (n/2 +1) the term]/2

= [(20/2) th term + (20/2 +1) the term]/2

= [10 th term + 11 the term]/2

= (38 +38)/2 =38

Hence median of the given data is 38

Q8.If mean =52.08 and mode =51.6.Find Median.

Solution:

We have

Mode = 3 median – 2mean

51.6 = 3 median -2×52.08

3 median = 51.6 +104.16

3 median =155.76

median = 155.76/3 = 51.92

Class 10 Maths Standard Sample Paper 2024 Solutions 

 

Q9.LCM of 48,72 and 120 is ……

Solution:

48 = 2×2×2×2×3=2⁴×3

72 = 2×2×2×3×3=2³×3²

120=2×2×2×3×5=2³×3×5

LCM = 2⁴×3²×5=8×9×5 = 360

Q10.The sum of the difference of a rational number and an irrational number is…….

Solution:

As an example let a rational number is 2 and an irrational number is √2

The difference of both is (2 -√2) which is an irrational number

Therefore the sum of the difference of a rational number and an irrational number is an irrational number

Q11.Find the value of k for which (-4) is a zero of the polynomial x² -x(2k+2) is

Solution:

Since (-4) is a zero of the polynomial x² -x(2k+2)

Therefore x = -4 should satisfy the equation x² -x(2k+2) =0

(-4)² -(-4)(2k+2) =0

16 +8k +8 =0

8k + 24 =0

8k = -24

k = -24/8 = -3

Q12.The number of polynomials having zeroes as -2 and 5 is…….

Solution: If zeroes of a polynomial are α and β then polynomial is given as

x² – (α + β)x + αβ

The given zeroes α = -2 and β = 5

x² – (-2 + 5)x + (-2)5

x² – 3x -10

We can multiply the given polynomial by 1,2,3…(a constant number),so we can get infinite number of polynomials of having the zeroes -2 and 5.

As an example: 2x² – 6x -20,3x² – 9x -30,4x² – 12x -40…..

Q13.Find a quadratic polynomial when the sum of and the product of its zeroes is equal to 0 and √2 respectively.

Solution:Let the zeroes of the given polynomial are α and β

It is given α + β = 0 and αβ = √2

We know the polynomial with zeroes α and β is given as

x² – (α + β )x + αβ

x² – 0×x +√2

x²  +√2

Q14.Write a polynomial of the downward parabola .

Solution:The downward parabola is given as

ax² +bx + c,where a <0

Q15.Write the condition for inconsistent lines and give one example of those lines.

Solution:The pair of the lines a₁x+b₁y +c₁=0 and a₂x+b₂y +c₂=0 is inconsistent if

a₁/a₂ =b₁/b₂≠c₁/c₂

Example: 2x +5y + 8 and 4x +10y +3

Class 10 Maths Question Paper CBSE Half Yearly Exam 2022 With Solutions

Section B

(Part ll)

Solve all the four case studies:

Q16.

Case Study -1

Qutub Minar located in south Delhi, India, was built in the year 1193. It is a 72m high tower. Working on a school project, Charu and Daljeet visited the monument. They used trigonometry to find their distance from the tower. Observe the picture given below. Points C and D represent their positions on the ground in line with the base of the tower, the angles of elevation of the top of the tower(Point A) are 60° and 45° from points C and D respectively.

(i)Based on the above information, draw a well-labeled diagram.

Solution: Let the AB is the height of the Qutub Minar and BC is the distance of Charu and BD is the distance of Daljeet from the Qutub Minar

tan θ = perpendicular/base

tan 60° = AB/BC

√3 = 72/BC

BC = 72/√3  = 72√3 /3 =24√3 m

tan 45° = AB/BD

1= 72/BD

BD = 72 m

Therefore the distance of Charu and Daljeet from Qutub Minar are  24√3 m and 72 m respectively

(ii)Find the distance CD,BC and BD.(use √3 =1.73)

Solution: The distance BC and BD are already computed in (i)

BC = 24√3 = 24×1.73 =41.52 m

BD = 72 m

Therefore CD = BD -BC

CD = 72-41.52 =30.48 m

Class 10 Maths Question Paper CBSE Half Yearly Exam 2022 With Solutions

Case Study -2

Q17.A ferries wheel(or a big wheel in the united kingdom) is an amusement ride consisting of a rotating upright wheel with multiple passenger -carrying components(commonly reffrered to as passenger cars,carbons,tubs,capsules,gondolas or pods) attached to the rim in such a way that as the wheels turns,they are kept upright,usually by gravity.

After taking a ride in Ferris wheel,Aarty came out from the crowd and was observing her friends who were enjoying the ride.She was curious about the different angles and measures that the wheel will form.She forms the figgure as given below.(Solve any four)

(i) In the given figure ∠ROQ is:

(a) 60°        (b) 100°      (c)150°       (d)90°

Solution: ∠ROQ +∠QPR=180°

∠ROQ +30°   =180°

∠ROQ = 150°

(ii)∠RQP is equal to:

(a) 75°        (b) 60°      (c)30°       (d)90°

Solution:

∠RQP+∠QRP +∠QPR =180°

∠RQP=∠QRP(PR=PQ=tangents of the circle drawn from an external point)

2∠RQP  =180°-∠PQR=180°-30°=150°

∠RQP=75°

(iii)∠RSQ is equal to:

(a) 75°        (b) 75°      (c)100°       (d)30°

Solution:

∠RSQ =∠ROQ/2[angle subtended by equal chord QR  at the centre is twice of the angle at the circle)

∠RSQ =150°/2=  75°

(iv)∠QRP is equal to:

(a) 90°        (b) 70°      (c)100°       (d)60°

Solution:

∠PQR+∠QRP +∠QPR =180°

∠PQR=∠QRP(PR=PQ=tangents of the circle drawn from an external point)

2∠QRP  =180°-∠PQR=180°-30°=150°

∠QRP=75°

(v)∠ORQ is equal to:

(a) 30°        (b) 45°      (c)15°       (d)75°

Solution:

Considering the triangle QOR

∠ORQ =∠RQP(OR=OQ=radii of the circle)

∠ROQ+∠ORQ +∠RQP=180°

150°  +2∠ORQ =180°

∠ORQ = 15°

Case Study -3

Q18.Overweight and obesity may increase the risk of many health problems, including diabetes, heart disease, and certain cancers. The basic reason behind is diabetes, eating more junk foods, and less physical exercise. The school management give instruction to the school to collect the weight data of each student. During the medical check of 35 students from class X-A, their weight was recorded as follows(any four):

(i)The median class of the given data is:

(a) 44-46        (b) 46-48       (c)48-50      (d)None of these

(ii)The median weight of the given data is:

(a) 46.5        (b) 47.5       (c)46      (d)47

(iii)The mean  of the given data is:

(a) 45       (b) 45.8       (c)46.2      (d)46.8

(iv)Modal class of the given data is:

(a) 44-46        (b) 46-48       (c)48-50      (d)50-52

(v)While computing the mean of the given data,we assumed that the frequencies are:

(a)evenly distributed over all the classes

(b)centered at the class marks of the classes

(c)centered at the upper limits of the classes

(d)centered at the lower limits of the classes

Case Study -3(any four)

Q19.The given figure along side shows the path of a driver,when she takes a jump from the driving board.Clearly it is a parabola.

Annie was standing on a driving board,48 feet above the water level.She took a drive into the pool.Her height(in feet) above the water level at any time’t‘ in seconds is given by the polynomial h(t) such that

h(t) = -16t² +8t +k

(i)What is the value of k?

(a)0          (b)-48       (c)48        (d)49/-16

Solution: k is a constant in the given polynomial h(t) = -16t² +8t +k

We know the height of Annie at t=0 is 48 m above the water level

48 = -16×0² +8×0 +k

k =48

(ii)What time will she touch the water in the pool?

(a)30 seconds      (b)2 seconds     (c)1.5 seconds     (d)0.5 seconds

Solution:

When Annie touch the pool her height above the pool will be,h =0

Putting h =0 and k=48 in the hiven polynomial h(t) = -16t² +8t +k

0 = -16t² +8t +48

16t² -8t -48 =0

2t² -t -6 =0

2t² -4t+3t -6 =0

2t(t -2) +3(t-2) =0

(t-2)(t+3) =0

t =2, t= -3

Neglective t=-3 because time can not be negative

Therefore she will touch the pool in 2 seconds

(iii)Rita’s height(in feet) above the water level is given by another polynomial p(t) with zeroes -1 and 2.Then p(t) is given by:

(a) t² +t-2             (b)t² +2t-1     (c)24t² -24t+48     (d)-24t² +24t+48

Solutions:

The polynomial p(t) with zeroes α=-1 and β=2 is given by

t² -(α+β)t+αβ

=t² -(-1+2)t+(-1)2

=t² -t-2

We can multiply it by -24 we get the required polynomial with the same zeroes

p(t) = -24t² +24t+48

(iv)A polynomial q(t) with sum of zeroes as 1 and the product as -6 is modelling Anu’s height in feet above the water at any time t(in seconds).Then q(t) is given by

(a) t² +t+6             (b)t² +t-6     (c)-8t² +8t+48     (d)8t² -8t+48

Solutions:

The polynomial q(t) with zeroes α and β is given by

q(t)=t² -(α+β)t+αβ

=t² -(1)t+(-6)

=t² -t-6

We can multiply it by -8 we get the required polynomial with the same zeroes

q(t) = -8t² +8t+48

(v)The zeroes of the polynomial r(t) = -12t² +(k-3)t +48 are negative of each other.Then k is:

(a)3          (b)0          (c)-1.5        (d)-3

Solution:

The polynomial r(t) with zeroes α and β is given by

r(t)=t² -(α+β)t+αβ

Since it is given that β = -α

r(t) = t² -(α-α)t+α(-α)

r(t) =t²  – α²

Comparing with the given polynomial r(t) = -12t² +(k-3)t +48

k-3=0

k= 3

Class 10 Maths Question Paper CBSE Half Yearly Exam 2022 With Solutions

Section C

(Part lll)

Q20.45 roses,65 carnations and 50 tulips are used to prepare identical flowers arrangments. What is the maximum number of such arrangements that can be prepared?

Solution: Here we have to arrange identical arrangements by using 45 roses,65 carnations, and 50 tulips

Therefore maximum number of such arrangements is the HCF of all the given numbers of the flowers

45= 3²×5

65 =13×5

50 = 5²×2

HCF(45,65,50) = 5

Hence the required number of such arrangements are 5

Q21.Find the zeroes of polynomial f(x) =4√3 x² +5x -2√3, and verify the relationship between the zeroes and the coefficients.

Solution:

The given polynomial is f(x) =4√3 x² +5x -2√3

Finding the zeroes of the given polynomial by factorizing it

4√3 x² +5x -2√3

=4√3 x² +8x -3x-2√3

=4x(√3 x+2) -√3(√3x +2)

=(√3 x+2) (4x -√3 )

The zeroes of the polynomial are -2/√3 and √3/4

Comparing the standard quadratic equation ax² +bx +c with the given polynomial

f(x) =4√3 x² +5x -2√3

a =4√3 , b =5 and c =-2√3

The relationship between the coefficients and the zeroes α and β are given by

α+β = -b/a and αβ = c/a

-2/√3 + √3/4 =-5/4√3  and -2/√3 × √3/4=-2√3/4√3

(-8+3)/4√3=-5/4√3  and -2√3/4√3 = -2/4

-5/4√3 =-5/4√3 and -1/2 = -1/2

Verified

Q22.Solve the equations for x and y:

3x +2y =1, 7x -y = -26

Solution:The given equations are

3x +2y =1…….(i)

7x -y = -26……(ii)

Multiplying the equation (ii) by 2 we get equation (3)

14x -2y = -52….(iii)

Adding equation (iii) to equation (i)

17x=-51

x = -3

Putting the value x=-3 in the equation (i)

3×-3 +2y =1

-9 +2y =1

2y = 10

y= 5

Therefore solutions of the given pair of the equation is x =-3 and y=5

Q23.Prove that:

Sin⁴A-sin²A = cos⁴A – cos²A

Solution:

The given trigonomentric equation is

Sin⁴A-sin²A = cos⁴A – cos²A

Taking the LHS

Sin⁴A-sin²A

=(sin²A)² – sin²A

=(1-cos²A)²-(1-cos²A)

=1 +cos⁴A -2cos²A -1 +cos²A

=cos⁴A -cos²A=RHS

Hence proved

Q24.Let s denote the semi perimeter of a triangle ABC in which BC =a,CA=b,AB =c,if a circle touches the sides BC,CA,AB at D,E,F respectively.Prove that BD = s -b

Solution:

 

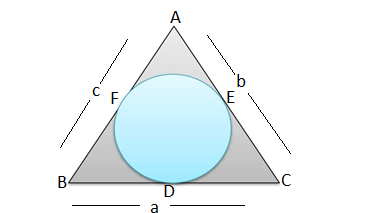
It is given that s is the semi perimeter of a ΔABC,in which BC =a,CA=b,AB =c

s = (a +b+c)/2

2s = a +b+c ……(i)

Let BD = x

Tangents drawn from an external point to the circle are equal

BD = BF =x

AF = AB -BF =c-x

AF = AE =c-x

DC = a -x =CE

AE +CE = b

c-x +a -x =b

-2x = b -(c +a)

2x = c+a-b

Substituting the value of c+a = 2s-b from equation (i)

2x = 2s-b -b

2x = 2s -2b

x = s-b

BD = s -b

Hence Proved

Q25.Find the mean of the following:

Mid Value	2	3	4	5	6
Frequency	49	43	57	38	13

Solution:

Mid Value(x)	Frequency(f)	fx
2	49	98
3	43	129
4	57	228
5	38	190
6	13	78
	N=220	∑fx=623

 

Mean =∑fx/N

Mean =623/220 =2.83

(Part iv)

Q26.A school has five houses A, B, C, D, and E. A class has 23 students,4 from house A,8 from house B,5 from house C,2 from house D, and the rest from house E.A single student is selected at random to be the class monitor. The probability that the selected student is not from A,B and C.

Solution: Total number of students in the class = 23

The number of students from the house A,B and C is =4+8+5=17

The number of students from house E = 23 -17 =6

P(students who are not from A,B, and C houses) =Number of students from house E/Total number of students

P(students who are not from A,B, and C houses)=6/23

Q27.The daily expenditure of 100 families is given below.Calculate f₁ and f₂ if the mean daily expenditure is Rs 188.

Expanditure(Rs)	140 -160	160-180	180-200	200-220	220-240
Number of Families	5	25	f1	f2	5

Solution:

Expenditure(Rs)	Class Mark(x)	No. of families(f)	fx
140-160	150	5	750
160-180	170	25	4250
180-200	190	f1	190 f1
200-220	210	f2	210 f2
220-240	230	5	1150
		N=35+ f1+f2=100	∑fx=6150+190 f1+210 f2

Mean =∑fx/N

Since No. of families are given 100 and the mean expanditure of them is 188

35+ f₁+f₂=100

f₁+f₂= 100 -35 =65…….(i)

188 = (6150+190 f₁+210 f₂)/100

6150+190 f₁+210 f₂= 18800

190 f₁+210 f₂= 18800 -6150=12650…..(ii)

Putting the value f₂= 65 -f₁ from equation (i) in equation (ii)

190 f₁+210(65- f₁) =12650

190 f₁-210f₁+13650=12650

20f₁ = 1000

f₁ = 50

Putting the value of f₁ =50 in equation (i) ,we get f₂ =15

Q28.Prove that:

(cos³A +sin³A )/(cosA +sinA )+(cos³A-sin³A )/(cosA -sinA ) = 2

Solution:We have to prove that

(cos³A +sin³A )/(cosA +sinA )+(cos³A-sin³A )/(cosA -sinA ) = 2

Taking LHS

(cos³A +sin³A )/(cosA +sinA )+(cos³A-sin³A )/(cosA -sinA )

Applying the identities

a³ +b³ = (a +b)(a² +b² -ab)

a³-b³ = (a -b)(a² +b² +ab)

⇒(cosA +sinA)(cos²A +sin²A-sinA.cosA)/(cosA +sinA) + (cosA -sinA)(cos²A +sin²A+sinA.cosA)/(cosA -sinA)

=(1 -sinA.cosA) + (1 +sinA.cosA)

=2= RHS

Hence Proved

Q29.If sinθ = p/q then the value of tanθ +secθ = ?

Solution:

Given that

sinθ = p/q

Since sinθ = perpendicular(p)/hypotenuse(h)

Base(b) =√(h²-p²) =√(q²-p²)

tanθ =perpendicular/base=p/√(q²-p²),secθ =hypotenuse/base =h/b =q/√(q²-p²)

tanθ +secθ =p/√(q²-p²) +q/√(q²-p²)

tanθ +secθ=(q+p)/√(q²-p²)

tanθ +secθ=(q+p)/√(q-p)(q+p)

tanθ +secθ=√[(q+p)/(q-p)]

 

OR

x = a sinθ, y = b tanθ

Prove that a²y² – b²x² = x²y²

Solution:

We have to prove

a²y² – b²x² = x²y²

Given that

x = a sinθ, y = b tanθ

Putting the value of x and y in the LHS

a²(b tanθ)² – b²(a sinθ)²

=a²b²tan²θ -a²b²sin²θ

=a²b²(tan²θ -sin²θ)

=a²b²(sin²θ/cos²θ -sin²θ)

=a²b²(sin²θ -cos²θsin²θ)/cos²θ

=a²b²sin²θ(1 -cos²θ)/cos²θ

=a²b²(sinθ/cosθ)²sin²θ

=a²b²tan²θsin²θ

=(asinθ)²(b tanθ)²

=x²y²=RHS

Hence Proved

Q30.A vertical tower is surmounted by a flag staff of height h meteres.At a point on the ground,the angle of elevation of the bottom and top of the flagstaff are α and β respectively. Prove that the angle of the tower is

h tanα/(tan β -tan α)

Solution;

 

Solution:Let AB is the height of the tower

The point on the ground is C

tan α= AB/BC

BC = AB/tanα…. (1)

tanβ = (AB+h)/BC

BC = (AB+h)/tanβ…. (2)

From equations (1) and (2)

AB/tanα = (AB+h)/tanβ

ABtanβ = tanαAB+htanα

AB(tanβ-tanα) = htanα

AB = htanα/(tanβ-tanα)

Height of the tower = htanα/(tanβ-tanα)

Q31.Determine the value of k so that the following linear equations have no solution

(3k +1)x +3y -2 =0,(k² +1)x +(k -2)y -5=0

Solution:The pair of linear equations a₁x+b₁y +c₁=0 and a₂x+b₂y +c₂=0 have no solutions if

a₁/a₂ =b₁/b₂≠c₁/c₂

Comparing the given pair of linear equations (3k +1)x +3y -2 =0,(k² +1)x +(k -2)y -5=0

a₁=3k +1,a₂ =k² +1,b₁=3,b₂=k -2,c₁=-2 ,c₂=-5

(3k +1)/(k² +1)=3/(k -2)≠-2/-5

Taking

(3k +1)/(k² +1)=3/(k -2)

(3k +1)(k -2)=3(k² +1)

3k²-6k +k-2 = 3k²+3

-5k -2 =3

-5k -5 =0

5(-k +1) =0

k = 1

Taking

3/(k -2)≠-2/-5

-2k +4 ≠-15

-2k ≠-15-4

-2k≠-19

k≠-19/2 =-9.5

Therefore for the value of k=1 and k≠-9.5 the given pair of linear equation have no solutions

Q32.Prove that √5 + √2 is an irrational number.

Solution:

Let (√5 + √2) is a rational number

Hence √5 + √2 =a/b[where a and b are co-prime number]

Squiring both sides

(√5 + √2)² =(a/b)²

5 +2 +√10 =a²/b²

7 +√10 =a²/b²

√10 =a²/b²-7

√10 =(a²-7b²)/b²

Irrational number =Rational number

It is impossible because it is against our assumption

Therefore (√5 + √2) is an irrational number

(Part v)

Q33.A circle is inscribed in ΔABC touching AB,BC and AC at P,Q and R respectively.If AB =10 cm,AR =7 cm and CR =5 cm.Find the length of BC and the radius of circle.

Solution: Given that in ΔABC,AB =10 cm,AR =7 cm and CR =5 cm

Since the tangents drawn from an external point to the circle are equal

CR =CQ=5 cm

BQ =BC -CQ = BC -5

BP =BQ =BC -5

AP =10-BP=10-(BC -5) =BC -5

AP =AR

BC -5 =7

BC =12

Drawing two radii of the given circle RO and PO

OR =PO =r

Considering the ΔAOR and ΔAOP

ΔAOR and ΔAOP are  right triangles[tangent ⊥ radius ]

In ΔAOR

AO² = 7²+ OR²=49+ r²

AO²= 49 +r²…….(i)

Similarly in ΔAOP

AO²= AP² +r²=(AB -BP)² +r²

AO²=[(10-BP)²+r²]

BP =BC-5 =12-5=7

AO²=[(10-7)²+r²]

Putting the value of BC =12

 

 

 

Q34.Two men are either side of a 75 m high building and in line with base of building observe the angles of elevtion of the top of the building as 30° and 60°.Find the distance between the two men.[use √3 =1.73]

Solution:

Let the buiding is PQ and two men are located at R and S such that the angle of elevation from the point R is 60° and 30° from the point S

The height of building(PQ) is given 75 m

tan 60° = PQ/QR

√3 = 75/QR

QR = 75/√3 = 25√3 = 25×1.73=43.25 m

tan 30° = PQ/QS

1/√3 = 75/QS

QS = 75√3  = 75×1.73=129.75 m

The distance between the two men ,RS =43.25 m+129.75 m=173 m

Or

From the top of a 50 m high tower,the angles of depression of the top and bottom of a pole are observed to be 30° and 45° respectively.Find the height of the pole.[√3 =1.73]

Solution:

Let the height of the tower is AB and the height of the pole is CD, height of the tower is given 50 m

Angles of depression from the top of the tower to the top and bottom of the pole are 30° and 45°

Drawing a line DE parallel to BC

CD = BE

Angle of depression =Angle of elevation

tan 30°= AE/DE

1/√3 = AE/DE

1/√3 = (50-BE)/DE…….(i)

tan 45°= AB/BC

1 = 50/BC

BC =50

BC = DE=50 m(BCDE is a rectangle)

Putting the value of DE in equation (i)

1/√3 = (50-BE)/50

50√3 -BE√3 =50

BE√3 =50√3 -50

BE =50(√3 -1)/√3

BE= 50(1.73 -1)/1.73

BE = 50×0.73/1.73 ≈21.09

BE =CD =21.09 m

Hence the height of the pole is 21.09 m

Q35.In a coeducational school, there are 2800 students. If in a year the number of boys were to increase by 5% and that of the girls by 10%, the school would have 3000 students. Find the original number of boys and girls studying in the school.

Solution: Let the original number of boys and girls studying in the school are x and y

The total number of students in the school are given 2800

x + y = 2800…….(i)

If the number of boys was to increase 5% and the number of girls increase by 10% then the number of boys and girls will become (x +5x/100) and (y+10y/100) respectively and total number of students were increased to 3000

(x +5x/100) + (y+10y/100) =3000

x +x/20 +y +y/10 =3000

21x/20 +11y/10 =3000

21x + 22y = 60000……(ii)

Multiplying equation (i) by 21 ,we get equation (iii)

21x +21y = 58800 ….(iii)

Subtracting equation (iii) from equation (ii)

y  =1200

Putting y =1200 in equation (i)

x = 3000 -1200 =1800

Hence the original number of boys and girls in the school are 1800 and 1200 respectively

You can compensate us

Paytm number 9891436286

The money collected by us will be used for the education of poor students who leaves their study because of a lack of money.

NCERT Solutions for class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions