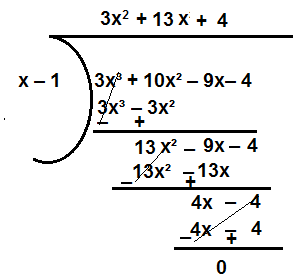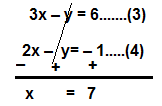Solution of class 10 maths question paper CBSE Board 2019

The solutions of class 10 maths question papers Set 3 CBSE Board 2019 will help you in your preparation of the CBSE board exam 2020-21. From the solutions of class 10 maths, question papers Set 3 CBSE Board 2019 all students will get the idea regarding the kind of questions posed in maths paper in the CBSE board exam 2020-21. All the questions in the post ‘solutions of Class 10 maths question paper Set-3 CBSE Board 2019‘ are explained by a specialist teacher of maths CBSE. The students who study earlier years question papers consistently get extra knowledge and confidence that reflects in their mark sheet of the board exam as brilliant marks.

Solutions of Class 10 maths question paper Set-3 CBSE Board 2019

Examining this post about the solutions of class 10 maths question paper of 2019, you will get illuminating from the solutions of the question paper of maths. Here each question of the question paper set 3 CBSE Board exam is clarified by bit by bit technique, notwithstanding, on the off chance that you face any sort of issue kindly don’t spare a moment to write your comment. In the event that you are intending to accomplish more than 90 % marks in science and maths, for this, here we have likewise given link of our digital books for maths and science solutions, you can get it at the negligible cost of Rs 50 only, thusly of this, you will get free examination material on your email or you can WhatsApp us after purchasing the e-book or you can contact for any sorts of help, our WhatsApp number is 9891436286 and 7303064710.

 

 

Class 10 unsolved maths question paper Set 3 2019 CBSE board exam

Science and Maths NCERT solutions for Class 9 ,10 and 11 classes

e-book of physics and chemistry notes class 10 at the cost of Rs 50

Class 10 maths NCERT solutions and Important questions of maths of the chapters 1,2,3,4,8 and 9

Solution of class 10 maths question paper CBSE Board 2019

The time allowed: 3 hours                                                                                                                           Maximum marks: 80

General Instructions:

(i) This question paper comprises four sections- A, B, C, and D. This question paper carries 40 questions. All questions are compulsory.

(ii) Section A: Q.No. 1 to 6 comprises of 6 questions of 1 mark each.

(iii) Section B: Q. No. 7 to 12 comprises of 6 questions of two marks each.

(iv) Section C: Q.No. 13 to 22 comprises of 10 questions of three marks each.

(v) Section D: Q.No. 23 to 30 comprises of 8 questions of four marks each.

(vi) There is no overall choice in the question paper. However, an internal choice has been provided in questions of 2 marks each, 2 questions of 3 marks each. 3 questions of 4 marks each. You have to attempt only one of the choices in such questions.

(vii) In addition to this, separate instructions are given with each section and question, whenever necessary.

(viii) The use of calculators is not permitted

 

Solution of class 10 maths question paper CBSE Board 2019

Section- A

Question numbers 1 to 6 carry 1 marks each.

1. Two positive integers a and b can be written as  a= x³y² and b= xy³.  x,y are prime numbers. Find LCM (a,b).

Ans. We are given the integers

a= x³y² and b= xy³

LCM(a,b) = x³y³

2.How many two digit numbers are divisible by 3.

Ans. The first two digit number in the series of two digit numbers divisible by 3 is 12

The first two digit number in the series of two digit numbers divisible by 3 is 99

The series of the two digir numbers divisible by 3 will be as following

12, 15,18,21…………..99

Let the number of total two digit numbers are = n

Applying the fomula for n th term of an AP.

a_n  = a + (n – 1)d

99 = 12 + (n – 1)3

3n –3 = 87

3n = 90

n = 30

Hence two digit numbers divisible by 3 are=30

3.In fig.1 DE ∥BC, AD = 1 cm and BD = 2 cm, What is the ratio of the ar(ΔABC) to the ar(ADE) ?

Ans. In ΔABC  we are given DE ∥BC

So, ∠ADC = ∠ABC (Corresponding angle)

∠AED = ∠ACB (Corresponding angle)

ΔABC ∼ΔADE (AA rule)

The ratios of the areas of two  similar triangles is the ratio of squares of their corresponding sides

AD = 1 cm. AB = BD + AD = 1 + 2 = 3 cm

Therefore the ratio of areas of ar(ΔABC) to the ar(ADE) is 1 : 9.

4. Find the coordinates of point A, where AB is the diameter of a circle whose center is (2,−3) and B is the point (1,4).

Ans. We are given AB is the diameter of the circle

The center of the circle divides the diameter in the ratio of 1 : 1

So, using section formula the co-ordinates of the midpoint(x.y) when co-ordinates of both ends of the line segment are  (x₁, y₁) and (x₂,y₂) are given, can be written as follows.

Therefore the coordinates of the center are (3/2,1/2)

5. For what values of k , the roots of the equation 3x²– 10x + k =0 are equal.

Ans. We are given the quadratic equation 3x²– 10x + k =0

The condition in a quadratic equation ax²+ bx + c =0 of equal roots is as follows

b²– 4ac = 0

Comparing the given quadratic equation, we have

a = 3, b= – 10 and c= k

(– 10)²– 4 ×3×k = 0

12k = 100

k = 25/3

Hence the required value of k is 25/3

6. Find A if tan 2A = cot ( A – 24º)

Or

Find the value of (sin²33º + sin²57º).

Ans. We are given the equation

tan 2A = cot ( A – 24º)

Since tanθ = cot(90º–θ)

So, the equation can be rewritten as following

cot (90º–2A) = cot ( A – 24º)

90º–2A = A – 24º

3A = 114

A = 38

Therefore the required value of A is 38º.

Or

We have to determine the value of sin²33º + sin²57

Since sinθ = cos(90º–θ)

∴ sin33º =  cos(90º–33º ) = cos 57º

Substituting the value of sin33º in the given expression

cos²57º + sin²57

= 1 ( since cos²θº + sin²θ)

Therefore the value of the given expression is 1.

Solution of class 10 maths question paper CBSE Board 2019

Section B

Question number 7 to 12 carry 2 marks each

Purchase your favourite mobile,laptops or Desktops in affordable EMI

7. Find, how many two-digit natural numbers are divisible by 7

Ans. The first two-digit natural number divisible by 7 is 21, if you face any difficulty in finding the last two digit numbers divisible by 7, then find it by the following way.

Last two-digit number  is 99

Divide it by 7, the remainder is 1

Subtract the remainder from 99 we get the last two-digit number divisible by 7 = 99 – 1= 98

The series of two-digit numbers divisible by 7 is written as follows

14,21,28…………98

Let the two-digit numbers divisible by 7 are n

Applying the formula for nth term of an AP.

a_n  = a + (n – 1)d

Where a = 7, d = 7, a_n  =  98

98 = 14 + (n –  1)7

7n = 91

n = 13

Hence the required numbers of two-digit numbers divisible by 7 are 13.

Or

If the sum of first n terms of an AP is n², then find its nth term.

Let the sum of nth term is represented by S_n

S =  n²

S₁ = 1² = 1, First term of AP = 1

S₂ = 2² = 4, Second term of AP = Sum of two terms – First term = 4 – 1 = 3

S₃ = 3² = 9, Third term of AP = Sum of 3 terms of an AP – Sum of two terms = 9 – 4 = 5

Therefore the AP is written as follows

1,3,5……….an

a = 1, d= 3-1=2

Applying the formula of nth term of an AP

Hence the nth term of the AP is 2n -1

8. A game consists of tossing a coin 3 times and noting the outcome each time. If getting the same result in all the tosses is a success. Find the probability of losing the game.

Ans.Total possible outcomes in tossing a coin 3 times (8) – (HHH),(TTT),(HHT),(TTH),(HTH)(THT),(HTT),(THH)

The outcome of the same result(2)-(HHH),(TTT)

Since the same results in tossing the coin is a success

Let the probability of winning the game is P(E)

Let the probability of losing game is   

We know

Therefore the probability of losing the game is 3/4

9. Find the ratio in which the segment joining the points(1,-3) and (4,5) is divided by x-axis also find the coordinates of this point on the x-axis

Ans. The  y coordinates of the point on x-axis is 0, so let the point  that divides the line segment on the x-axis is = (x,0)

Applying the section formula

Where k is the fraction which shows the ratio the point (x,y) divides the line segment between  (x₁, y₁)  and (x₂, y₂)

(x₁, y₁)   (x₂, y₂) = (1,-3) and (4,5) and (x,0) = (x,y)

Since known value is y =0, so applying the section formula for y co-ordinate, we get

5k – 3 = 0

Therefore the ratio is 3 : 5  by which  the x-axis divides the line segment joining the points (1,-3) and (4,5)

 

10. A die is thrown once. Find the probability of getting a number which (i) is a prime number (ii) lies between 2 and 6.

Ans. (i) The total possible outcomes when a die is thrown once are = 6(1,2,3,4,5 and 6)

Among the possible outcomes, the prime numbers are = 3(2,3 and 5)

Favorable outcomes are = 3

Let the probability of the event that the outcome is prime number = P(E)

(ii) The total possible outcomes when a die is thrown once are = 6(1,2,3,4,5 and 6)

Among the possible outcomes, the  numbers which lies between 2 and 6 are = 3(3,4 and 5)

Favorable outcomes are = 3

Let the probability of the event that the outcome is between 2 and 6 is = P(E)

11. Find c if the system of the equation cx + 3y + (3 – c) = 0 ; 12x + cy –  c = 0 has infinity many solutions.

Ans. The condition of infinite solutions of two standard linear equations  a₁x +b₁y +c₁ and  a₂x +b₂y +c₂ is following

Comparing the given pair of linear equation with the standard pair of linear equations cx + 3y + (3 – c) = 0 ; 12x + cy –  c = 0

a₁  = c, b₁ = 3 , c₁ = 3 – c and a₂ = 12, b₂ = c, c₂ = -c

c² = 36

c =  ± 6

Therefore the given pair of the linear equation has infinite solutions for c = ± 6

12. Find the HCF of 1260 and 7344 using Euclid’s algorithm.

Ans. According to Euclid’s algorithm, any positive integer can be written in the form of a = bq +r, where a > b and 0 ≤ r < b, if r = 0 then b is the HCF of the given numbers

Dividing 7344 by 1260 subsequently by the remainder

7344=1260×5+1044

1260=1044×1+216

1044=216×4+180

216=180×1+36

180=36×5+0

So by Euclid’s algorithm

HCF of 1260 and 7344 is 36

 

Or

Show that every positive odd integer is of the form  (4q + 1)  or (4q  +3), where q is some integer.

Ans. According to Euclid’s division lemma, any positive number(a) can be written in the  form of  bq + r

a = bq + r such that 0 ≤ r < b ,where b is also another positive integer

Let b = 4

Therefore the possible value of b is 0,1,2 and 3

Corresponding values of the positive integers will be as following

Substituting the value of r(0,1,2 and 3) in bq + r

4q or 4q + 1 or 4q + 2 or 4q + 3

Among the above possible value of positive integers, the odd numbers are following

4q + 1 or 4q + 3

Hence, it has been proved that any positive odd integer can be written in the form of  (4q + 1)  or (4q  +3)

Solution of class 10 maths question paper CBSE Board 2019

Section C

Question number 13 to 22 carry 3 marks each

13. Find all the zeroes of the polynomial 3x³ + 10x² – 9x– 4 if one of its zero is 1.

Ans. The polynomial given to us is 3x³ + 10x² – 9x– 4 one of its zero 1

If one of its zero is 1 then one of its factors must be (x – 1)

Therefore dividing the given polynomial by (x – 1)

Factorizing the quotient 3x ² + 13x + 4

3x ² + 12x +x + 4

3x (x + 4) + 1( x + 4)

(x + 4)( 3x + 1)

x + 4 = 0 ⇒ x = – 4

Therefore the zeroes of the given polynomial are 1, – 4  and – 1/3

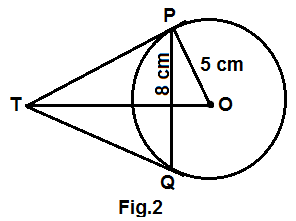
14. PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersects at a point T(see fig.2). Find the length TP.

 

Ans.

Ans. PO is the radius of the circle in the given fig.2 and TP is the tangents drawn at P

We know TP ⊥ PO ( Radius of the circle is perpendicular on tangent)

Joining the point Q to O

 

 

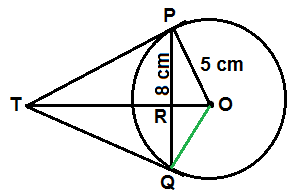
Let OT and PQ intersect at R

Considering the ΔPTR

TP = TQ ( Tangents drawn from an external point of the circle)

TR = TR (common)

∠PTR = ∠QTR (TO is the bisector of the ∠PTQ)

ΔPTR ∼ ΔQTR (SAS rule)

Therefore we can understand that TO is the perpendicular bisector of PQ

In ΔPRO

PR = 8/2 = 4 cm and we are given us OP = 5 cm

OR = 3 cm

In ΔOTP

OT = TR + OR = TR + 3

Substituting the value of OT in the  equation just above

TP² = (TR +3)² – 25

TP² = TR² + 9 + 6TR – 25

TP² = TR²  + 6TR – 16………(i)

In ΔPTR

TP² = TR² +PR² = TR² + 4² = TR² + 16….(ii)

From (i) and (ii), we have

6TR = 32

Putting the value of TR in equation (ii), we have

Hence, the length of TP is 20/3 cm.

 

15. Prove that          is an irrational number, given that    is an irrational number.

Ans.

Therefore it can be written in the form of P/Q, where P and Q are co-prime numbers

 

Irrational = Rational

It is impossible , therefore whatever we have supposed is wrong ,so the given number is an irrational number.

16. Prove that  (sinθ + cosec θ)² + (cosθ + secθ)² = 7 + tan²θ + cot²θ

Ans. We have to prove that

(sinθ + cosec θ)² + (cosθ + secθ)² = 7 + tan²θ + cot²θ

Taking the LHS

(sinθ + cosec θ)² + (cosθ + secθ)²

Applying the identity (x + y)² = x² + y² + 2xy

Sin²θ  + cosec²θ  + 2sinθ .cosecθ  + cos²θ  + sec²θ + 2cosθ .secθ

cosec²θ    + sec²θ + 5

Applying the identities cosec²θ  = 1 +  cot²θ  and sec²θ  = 1 +  tan²θ

1 +  cot²θ + 1 +  tan²θ + 5

7 + tan²θ +   cot²θ = RHS

Hence proved

Or Prove that ( 1 + cot A  – cosec A)(1 + tan A  +  sec A) =  2

Ans. We have to prove that

( 1 + cot A  – cosec A)(1 + tan A  +  sec A) =  2

Taking LHS

( 1 + cot A  – cosec A)(1 + tan A  +  sec A)

Applying the following formulas

Applying the identity x²– y² = (x + y)(x – y)

Since sin²A + cos²A = 1

= 2 = RHS

Hence proved

17. A father’s age is three times the sum of the ages of his two child.After 5 years his age will be two times the sum of their ages.Find present age of the father.

Ans.

Let the age of father is x and sum of the ages of both child is  y

According to first condition

x = 3y ……(1)

After 5 years the sum the age of the father is x + 5 and sum of the ages of his sun is = y + 5 + 5= y + 10

According to second condition

x + 5  = 2( y + 10)

x – 2y = 15………(2)

From (1) and (2), we have

y = 15 and x = 45

Therefore the present age of his father  is = 45 years

OR

A fraction becomes      when 2 is subtracted from the numerator and it becomes      when1 1 is subtracted from the denominator. Find the fraction.

Ans. Let the numerator of the fraction is x and  its denominator is y

The fraction is       

According to first condition

Simplifying the (1)  and (2) equations

3x – 6 = y

3x – y = 6…….(3)

2x = y – 1

2x –  y= – 1…..(4)

Subtracting  (4) from (3)

 

 

 

 

Putting the value of x = 7 in the equation (3)

3 × 7 – y = 6

y = 21 – 6 = 15

Therefore the numerator of the fraction is 7 and its denominator is 15

Hence the required fraction is     

 

18. Find the point on the y-axis which is equidistant from the points (5,-2) and (-3,2).

Ans. The x co-ordinate of the point on y-axis is 0, so we  let the co-ordinates of the point on y-axis is (0,y)

It is given to us that the point (0,y) is equidistant from (5,-2) and (-3,2)

The distance between (0,y) and  (-3,2) =  The distance between (0,y) and  (5, –2)

Applying the distance formula

Squaring both sides and simplifying

9 + y² + 4 – 4y = 25  + y² + 4 + 4y

8y  = 16

y = 2

Therefore the required co-ordinates of the point on y-axis are (0, 2)

 

OR

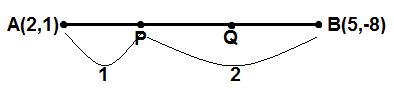
The line segment joining the points A(2,1) and B(5,-8) is trisected at the points P and Q such that P is nearer to A.If P also lies on the line given by 2x-y+k=0, find the value of K.

Ans. We are given the co-ordinates of the end points of  a line segments A(2,1) and B(5,-8) and P and Q trisect it

As it is shown in the fig. P divides the line segment AB in the ratio of 1 : 2

Let the coordinates of P  are (x,y), so applying the section formula

Where k is the fraction showing the ratio between two parts of a line segment divided by a point (x,y) and   (x_1,y₁ ) and (x_2,y₂) are the end  points of the line segment.

 (x_1,y₁ ) = (2,1) and  (x_2,y₂) = (5,-8), k= 1 : 2

Therefore coordinates of the point P are (3, –2)

We are also given that P(3, –2) lies on the line 2x-y+k=0, so the co-ordinates of P must satisfy the equation

2x-y+k=0

Putting the values x = 3 and y = –2 in the equation

2 ×3 + 2 + k = 0

k = – 8

Hence, the required value of k is – 8

 

19. Find the mode of the following frequency distribution

Class	0 – 10	10-20	20-30	30-40	40-50	50-60	60-70
Frequency	8	10	10	16	12	6	7

 

Ans.

Class	Frequency
0-10   10-20   20-30   30-40   40-50   50-60   60-70	8   10   10   16   12   6   7

 

Applying the formula for calculating Mode.

Where

f₁ = 16 (Frequency of modal class)

f₀  = 10(Frequency preceded to modal class)

f₂ = 12(Frequency succeeding to modal class)

h = 10(Size of modal class)

l= 30(lower limit of modal class)

Substituting these values in the formula

Mode = 30 + 6 = 36

Hence the mode of the given statistical data is 36

How to choose your subjects after 10 or 12 pass

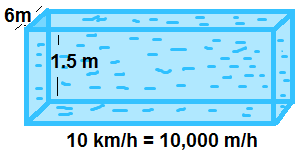
20. Water in a canal,6m wide and 1.5 m deep, is flowing with a speed of 10 km/hour. How much area will it irrigate in 3o minutes; if 8 cm standing water is needed?

Ans. Let the area to be irrigated is = A

The volume of water flowed through the canal in 30 minutes = Volume of 8 cm standing water in an area

The volume of water flowed through the canal in 1 hour(60 min) = 10,000 × 1.5 ×  6 = 90,000 cubic.m

The volume of water flowed through the canal in 1 min = 90,000/60 = 1500 cubic.m

The volume of water flowed through the canal in 30 min. = 30 × 1500 = 45000 cubic.m

The volume of 8 cm standing water in an area = A× height = 8A

Therefore

8A = 45000

Hence the area to be irrigated by the canal in 30 minutes is 5625 sq.m

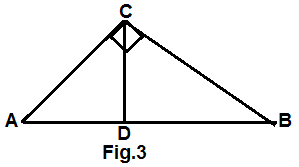
21. In fig.3, ∠ACB = 90º and CD ⊥ AB, prove that  CD² = BD × AD.

OR

If P and Q are points on side CA and CB respectively of Δ ABC, right-angled at C. Prove that (AQ² + BP²) = (AB² + PQ²)

Ans.

GIVEN. ΔABC in which ∠ACB = 90º and CD ⊥ AB

TO PROVE .CD² = BD × AD.

Hint: You can get the idea what you  have to do first, just see the sides in CD² = BD × AD, all sides are of triangle ADC and of triangle BDC, so considering this triangle for solving the problem

PROOF. We know the theorem if ∠ACB = 90º and CD ⊥ AB in ΔABC then ΔADC ∼ ΔCDB

So, applying the rule of similar triangles

CD² = BD × AD.

Hence proved

 

OR

If P and Q are points on side CA and CB respectively of Δ ABC, right-angled at C.Prove that (AQ² + BP²) = (AB² + PQ²)

 

Ans.

GIVEN. P is a point on side AC and Q is the point on BC of Δ ABC

∠ACB = 90º

CONSTRUCTION. Joining P to Q, A to Q and P to B

TO PROVE.  (AQ² + BP²) = (AB² + PQ²)

PROOF. Since ∠C  = 90º

In ΔAQC

AQ² = AC² + QC²……….(1)

In ΔPQC

PQ² = PC² + QC²……..(2)

In ΔPCB

BP² = PC² + BC²…… . .(3)

In ΔABC

AB² = AC² + BC²……..(4)

Hint: Get the idea what are the operations you have to do of these equations from (AQ² + BP²) = (AB² + PQ²)⇒AQ² – PQ² = AB² – BP², it is clear you have to subtract equation (2) from equation (1) and eq.(3) from eq.(4)

Subtracting equation eq.(2) from eq.(1) and eq.(3) from eq.(4)

AQ² – PQ² = AC²  – PC²…..(5)

AB² – BP² = AC² – PC² …..(6)

From (5) and (6)

AQ² – PQ² = AB² – BP²

AQ² + BP² = AB² + PQ²

Hence proved

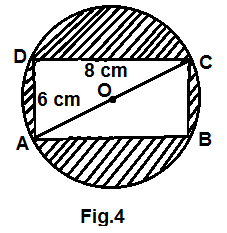
22. Find the area of the shaded region in fig.4, if ABCD is a rectangle with sides 8 cm and 6 cm and O is the center of the circle.(Take π = 3.14)

Ans. The area of shaded region = Area of the circle – Area of rectangle

AC is the diameter of the circle as well as diagonal of the rectangle

Therefore applying Pythagoras theorem

So, the radius of the circle is = AC/2 = 5 cm

Area of the circle = πr²  = 3.14 × 5² = 3.14 ×  25 = 78.5 sq.cm

Area of the rectangle is = Length × Breadth = 8 × 6 = 48 sq,cm

The area of shaded region = Area of the circle – Area of rectangle =

78.5 sq.cm – 48 sq,cm = 30.5 sq.cm

Hence the area of shaded region in the given fig. is 30.5 sq.cm

Solution of class 10 maths question paper CBSE Board 2019

Section-D

Question number 23  to 30  carry 4 marks each

 

Ans.We are given that

Applying the relationship between tanθ and secθ

 

Hence the value of secθ + tanθ is 2x

 

24.Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides

Ans.

GIVEN.  ΔABC ∼ ΔPQR

 

CONSTRUCTION. Drawing AM ⊥ BC and  PN ⊥ QR

TO PROVE.

 

 

PROOF.

Considering ΔABM and ΔPQN

∠B = ∠Q

∠AMB = ∠PNQ

ΔABM ∼ ΔPQN (AA Rule)

According to the rule of similar triangles

We are given ΔABC ∼ΔPQR

According to the rule of similar triangles

From (1) ,(2) and (3)

So,

Hence proved

25.The following distribution gives the daily income of 50 workers of a factory:

Daily Income (in ₹)	200-220			220-240				240-260			260-280	280-300
Number of workers	12					14		8			6	10

 

Convert the distribution above to a’ less than type’ cumulative frequency distribution and draw its ogive.

Ans. Calculating the less than frequency  to each upper limit of the class interval of the income of workers by adding a column less than CF

Income Less than	Frequency	Less than CF
220   240   260   280   300	12   14   8   6   10	12   26   34   40   50

 

Showing the upper limit of the class interval on x -axis and cumulative frequency on y-axis. Locating the points (220,12),(240,26),(260,34),(280,40) and (300,50) on the graph then joining all the points by a smooth hand, we get a less than ogive  of the daily income of the workers.

OR

The table below shows the daily expenditure on food of 25 households in a locality.find the mean daily expenditure on food.

Daily Expenditure (in rupee):	100-150	150-200	200-250	250-300	300-350
Number of Households:	4	5	12	2	2

 

 

Ans.

Daily Expenditure (in rupee):	Number of Households (f)	Class Mark(x)	fx
100 – 150	4	125	500
150 – 200	5	175	875
200 – 250	12	225	2700
250 – 300	2	275	550
300 – 350	2	325	650
	N= 25			∑fx=5275

Applying the formula of the direct method of calculating the mean of the above data.

Mean daily expenditure of  the 25 households is Rs 211

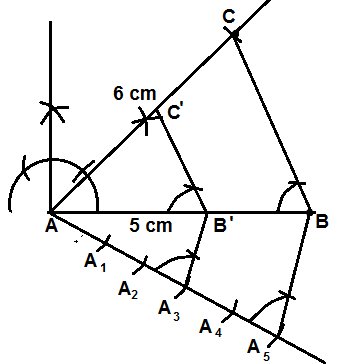
26. Construct a ΔABC in which CA=6cm, AB=5cm and ∠ BAC=45. Then construct a triangle whose sides are 3/5 th of the corresponding sides of the ΔABC.

Ans.

 

CONSTRUCTION. The steps of construction are following

STEP 1. Drawing a line AB of 5 cm.

STEP2. Drawing a ∠ BAC=45º

STEP3. Drawing an arc  AC of the radius 6 cm taking A as centre.

STEP 4. Joining  B to C

STEP5. Drawing an acute angle bellow the line segment AB on the vertex A.

STEP 6. Drawing the subsequent arcs of equal lengths  AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅

STEP 7. Joining  A₅   to  B

STEP8. Drawing  an angle  on   A₃   such that  ∠AA₅B ∼ ∠A A₃B’

STEP 9.Constructing an angle on B’ such that ∠ABC ∼ ∠AB’C’ , a triagle  ΔAB’C’ is formed which is similar to ΔABC and  3/5 th of it.

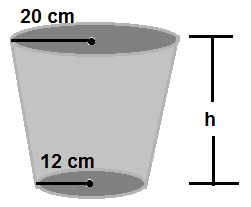
27. A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm³. The radii of the top and bottom of the circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of metal sheet used in making it.(Use π = 3.14)

Ans.

We are given the capacity(V) of the bucket = 12308.8 cm³

Using the formula of volume of the frustum

Radius of upper circular end  r₁ = 20 cm, Radius of lower circular end  r₂ = 12 cm and height h = ?

Substituting all values in the formula

36926.4 = 3.14h(400 + 144 +240)

36926.4 = 3.14h × 784

2461.76h = 36926.4

h = 15

So, the height of the frustum is 15 cm

Area of the metal sheet in making the bucket(A) = Curved surface area of the frustum + Area of base

A = πl(r₁ +r₂ ) + πr₂² where l is the slant height of the cone is calculated as follows

 

Substituting the values in the formula

A = 3.14 ×17(20 + 12) + 3.14 ×12² = 53.38× 32 + 3.14× 144 =1708.16 + 452.16 =2160.32

Therefore the metal sheet required in making the bucket is  2160.32 sq.cm

Hence the height of the bucket is 15 cm and area of metal sheet in making it is 2160.32 sq.cm

 

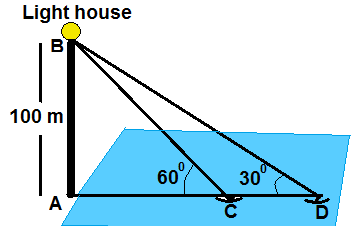
28.A man in a boat rowing away from a lighthouse 100 meters high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60º to 30º. Find the speed of the boat in meters per minute.(Use √3=1.732)

Ans.

Let the speed of the boat = x meters per minute

Since the speed of the boat = Distance traveled by the boat from C to D/Time taken from C to D

So, considering the triangle ABC

Considering the triangle ABD

AD = 100√3

CD = AD – AC

Hence the speed of the boat is 57.45 meters/minute

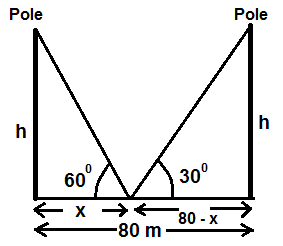
OR

Two poles of equal height are standing opposite to each other on either side of the road, which is 80 meters wide. From a point between them on the road, the angles of elevation of the top of the poles are 60º and 30º respectively. Find the height of the poles and the distances of the points from the poles.

Ans.

Let the height of both poles is = h and the distance of one of the pole is x  from the point of observation on the road and of another pole will be = 80–x

So, from the fig. we have

………..(1)

80–x = h√3

………(2)

from (1) and (2) we have

3x = 80–x

x = 20

Therefore the distances of both poles from the point of observation on the road are 20 m and 80–20 =60.

29. Two water taps together can fill the tank in      hours . The tap with a longer diameter takes 2 hours less than the tap with a smaller one to fill the tank separately. Find the time in which each tap can fill the tank separately.

Ans. Let the small tap alone can fill the tank in time = x hours

Longer diameter tap fills the tank in  = (x – 2)hours

In 1 hour smaller diameter tap can fill the tank in =          part of the tank

In 1 hour longer diameter tap can fill the tank in =        part of the tank

Both taps can fill the tank in 1 hour =          part of the tank

Both taps can  fill the tank in  hours

∴ In 1 hour both taps can fill the tank  =     part of the tank

According to question

8x² – 16x = 30x –  30

8x² – 46x + 30 = 0

4x² –23x + 15 = 0

4x² –20x –3x  + 15 = 0

4x(x – 5) – 3(x – 5) = 0

(x – 5)(4x – 3) = 0

x – 5 = 0 ⇒ x = 5

Neglecting x = 3/4 as (3/4 -2) is negative, so the time taken by longer diameter tap is 5 hours and by smaller diameter tap is  3 hours (5 -2= 3) .

OR

A boat goes 30 km upstream and 44 km downstream in 10 hours. In 13 hours, it can go 40 km upstream and 55 km downstream. Determine the speed of the stream and that of the boat in still water.

Ans. Let the speed of the boat = x km/h and speed of the stream = y km/h

The speed of the  boat in upstream is = (x – y) km/h

FIRST CONDITION. Distance traveled by boat in upstream = 30 km

Time is taken by boat in upstream =        hours

The speed of the  boat in downstream is = (x + y) km/h

Distance traveled by boat in downstream = 44 km

Time is taken by boat in downstream =      hours

According to the first condition

SECOND CONDITION. Distance traveled by boat in upstream = 40 km

Time is taken by boat in upstream =   

Distance traveled by boat in downstream = 55 km

Time is taken by boat in downstream =   

According to the second condition

 

The equations become

15a  + 22b = 5………(iii)

40a + 55b = 13…….(iv)

Multiplying (iii) by 8 and (iv) by 3 we get the (v) and (vi) equations

120a + 176b = 40…….(iv)

120a + 165b = 39…….(v)

Substracting (v) from (vi)

 

 

 

 

Putting this value of b in eq.(iii)

x – y = 5 ……(vii)  and x + y = 11……(viii)

Solving both (vii) and (viii) equations, we get

x = 8 and y = 3

Hence the speed of boat in still water is 8 km/h and speed of stream is 3 km/h

 

30. If the sum of  first four terms of an AP  is 40  and that of the first 14 terms is 280. Find the sum of its first n terms.

Ans.  We are given the sum of first 4 terms is = 40 and sum of first 14 terms is = 280

Applying the formula for the sum of AP

4a + 6d = 40

2a + 3d = 20……..(i)

14a + 91d = 280……(ii)

Multiplying eq.(i) by 7 we get eq.(iii)

14a + 21d = 140……(iii)

Subtracting equation (iii) from (ii)

70d = 140

d = 2

Putting the value of d in (i)

2a + 3 ×2 =20

2a = 14

a = 7

Putting the value of a and d in the formula of sum of AP.

= n(6 +n) = 6n + n²

Hence the sum of n terms of the given AP is 6n + n²

Best Amazon deals

 

 

You can also study

NCERT Solutions Class 10 Science from chapter 1 to 16

Download e-book of solutions of science and maths question papers 2019 and 2020 CBSE board

Solutions of Maths and Science 10 th class question papers 2019 and 2020 CBSE board

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions for class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions for class 9 science 

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

NCERT Solutions for class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT Solutions for Class 10 Science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

NCERT Solutions for class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT solutions for class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals

Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2

Class 12 Maths Important Questions-Application of Integrals

Class 12 Maths Important questions on Chapter 7 Integral with Solutions for term 2 CBSE Board 2021-22

Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22

Solutions of class 12  maths question paper 2021 preboard exam CBSE Solution