Solutions of math(Basic) question paper of class 10 CBSE Pre-Board Exam 2021

1. This question paper contains 36 questions divided into two parts A and B. All the questions are compulsory.

2. Part A consists of two sections-I and II. Section I has 16 questions of I mark each and section II has 4 case study-based questions. Each case-study-based questions have 5 subparts of 1 mark each.

3. Part-B consists of 16 questions- 6 questions of 2 marks, 7 questions of 3 marks, and 3 questions of 5 marks each.

4. There is no overall choice. However internal choices are provided in 5 questions of 1 mark, 2 questions of 2 marks, 2 questions of 3 marks and 1 question of 5 marks. You have to attempt only one of the alternatives in all such questions.

5. In cash study-based questions, you have to attempt only four out of five sub- parts.

6. Use of the calculator is not permitted.

7. Please write down the serial number of the question before attempting it.

Solution of Latest Sample paper Class 10 maths for Term 1 2021 CBSE board

Download free pdf of last years solutions of 4 maths question papers of class 10

NCERT Solutions of class 10 maths

NCERT Solutions of science Class 10

NCERT Solutions of Maths and Science from class 9 to 12

CBSE Class X Sample papers and Last years question papers of Science and Maths

Solutions of math(Basic) question paper of class 10 CBSE Pre-Board Exam 2021

Click for online shopping

Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc

Q1. HCF of co-prime numbers is always

Ans. HCF of co-prime number is 1, as an example 2 and 3 are co-prime numbers,  factors of 2 are = 2×1 and of 3 are = 3×1, 1 is the highest common factor between them, therefore 1 is the HCF of co-prime numbers.

Q2. Write a quadratic polynomial the sum of whose zeroes is -3 and product is -10

Ans. If the zeroes of the quadratic polynomial are a and b then the quadratic polynomial is given as

x² – (a+ b)x + ab

We are given a +b = -3 and ab = -10

x² -(-3)x + (-10)

=x² + 3x – 10

Q3. After how many decimal places will the decimal expansion of the number

47 / 2³ × 5² terminates.

Ans.  The fraction given to us is = 47/2³× 5² = 47/(2 ×5)² ×2 since the denominator is multiple of  (2 ×5)², so the decimal expansion of the given number will terminate after two places.

OR

Given that HCF (336, 54) is 6, Find LCM (336, 54).

Ans. The given numbers are 336 and 54 and their HCF is 6

The relationship between LCM ,HCF and numbers is as follows

LCM ×HCF = Product of numbers

LCM × 6 = 336 × 54

LCM = (336 ×54)/6 =336 ×9 = 3024

Q4. The diameter of a wheel is 1.54 m. How far will it travel in 200 revolutions?

Ans. The diameter of a wheel is = 1.54 m

Radius of the wheel,r = 1.54/2 = 0.77 m

The distance travelled by the wheel in one revolution is = circumference of the wheel = 2πr = 2 (22/7) ×0.77 = 44 ×0.11 = 4.84

The distance traveled by the wheel in 200 revolutions =200×4.84=968

Q5. Express 234 as the product of prime numbers.

Ans.234  = 2×3²×13

Q6. Find the area of a quadrant of a circle with a radius of 14cm. (Take π = 22/7)

Ans. We are given the radius,r of the circle = 14 cm

Area of the quadrant of the circle = πr²/4 = (22/7) (1/4)(14 ×14) =22×7=154 cm²

Q7. A pair of linear equations of two variables has a unique solution. What kind of lines will its graph represent?

Ans. If a pair of linear equations of two variables has a unique solution then then both lines will be intersecting lines and the co-ordinates of intersecting point is the solutions of the equations.

OR

For 3x – 7y = 10, Express y in terms of x.

Ans. The given equation is 3x – 7y = 10

– 7y = 10 -3x

y = (10 – 3x)/-7 = (3x -10)/7

∴ y = (3x -10)/7

Q8. On comparing the ratios of the coefficients, find out whether the pair of linear equations x – 2y = 0 and 3x + 4y – 20 = 0 is consistent or inconsistent.

Ans. The condition for a pair of linear equations a₁x  + b₁y + c₁=0, a₂x +b₂y +c₂=0 to be consistent is as follows

In the given equations x – 2y = 0 and 3x + 4y – 20 = 0

a₁=1  b₁ =-2, c₁=0, a₂=3 ,b₂ =4,c₂=-20

Therefore the pair of linear equations x – 2y = 0 and 3x + 4y – 20 = 0 is consistent

Q9. Probability of happening of an event is 3/7. What will be the probability of not happening of that event?

Ans. Let the event is E then the relationship between happening of probability P(E) and not happening of event is 

Since we are given P(E) = 3/7

Probability of not happening of event =4/7

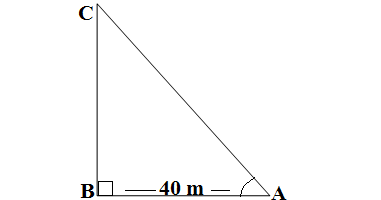
Q10. A surveyor wants to find out the height of a tower. He measures ∠A as tan A = 3/4. What is the height of the tower if A is 40m from its base as shown in the figure?

Ans. In ΔABC,we are given AB = 40 m and tan A =3/4

We have to find out height of the tower BC

Tan A =BC/AB = 3/4

BC : AB = 3 : 4

Let BC = 3x and AB = 4x

We are given AB = 40 m

4x = 40 ⇒x = 10

∴ AB = 3x = 3× 10 = 30 m

Hence height of the tower is 30 m.

Q11. The median of the given days with the observations in ascending order is 27.5. Find the value of x.

24, 25, 26, x + 2, x + 3, 30, 33, 37

Ans.  The median of the given data is,m = 27.5

The given data is 24, 25, 26, x + 2, x + 3, 30, 33, 37

Number of observations is = 8

Since number of observations is even number so applying the formula

2x +5 = 55

x = 25

Hence the value of x is 25

Q12. If a line segment AB is to be divided in the ratio 5:8 internally, we draw a ray AX such that ∠BAX is an acute angle. What will be the minimum number of points to be located at equal distances on ray AX?

Ans. The minimum number of points to be located at equal distances on ray AX are = 5 + 8 = 13

Q13. State the Pythagoras theorem.

Ans. In a right triangle

H² = P² + B²

Where H is the hypotenuse,B is the base and P is perpendicular

OR

If ΔABC ~ ΔDEF and ∠A = 45°, ∠C = 55°, then Find ∠E.

Ans. In ΔABC we are given ∠A = 45°, ∠C = 55°

According to angle sum property of the triangle

∠A + ∠B + ∠C = 180°

45° + ∠B + 55°= 180°

∠B = 180° – 100° = 80°

Since ΔABC ∼ ΔDEF

Therefore ∠E = ∠B = 80°

Q14. A bag contains 6 red balls and 5 blue balls. Once ball is drawn at random. What is the probability of getting a blue ball.

Ans. The total number of balls are = 6 red balls + 5 blue balls = 11 balls

Let the probabilty of drawing a blue ball is P(Blue)

Then P(Blue) = (Number of blue balls)/Total balls = 5/11

Hence probability of getting a blue ball is 5/11

OR

A die is thrown at once. What is the probability of getting an odd number?

Ans. If a die is thrown once then total possible outcome are =6(1,2…6)

The number of odd numbers among the total possible outcome =3(1,3 and 5)

Let the probability of getting an odd number is P(odd number)

P(odd number) = (number of odd numbers)/total outcomes= 3/6 = 1/2

Q15. If sinθ = 12/13, then find cosθ.

Ans.Sin θ = 12/13 = Perpendicular/hypotenuse

Let the Base is B  Perpendicular(P) is = 12x and hypotenuse(H)  =13

Applying the Pythagoras theorem

H² = P² + B² ⇒B = √(H² – P²) = √(13² -12²) =√(169 – 144) =√25 = 5

∴Cosθ = B/H =5/13

Q16. A pendulum swings through an angle of 30° and describes an arc 17.6 cm in length. Find the length of pendulum.

Ans. The length of arc(l) subtending an angle θ at the centre is given by

θ= 30°, l = 17.6 cm and r is the length of pendulum

r = 4 .8 cm

The length of the pendulum is 4.8 cm

OR

Find the area of a sector of a circle with a radius of 6 cm if the angle of the sector is 60°.

Ans. We are given the angle of sector, θ = 60° and radius of circle,r = 6 cm

Area of the sector ,A is given by the follwing formula

Hence area of the sector is 132/7 cm²

 

SECTION-II

Question numbers 17-20 are case study-based questions. Attempt any 4 subparts from each question. Each such part carries 1 mark.

Q17. Raman is stitching a kite-shaped patch on the cushion cover. Few questions came to his mind while stitching the patch. Give answers to his questions by looking at the figure.

 

(i) Raman stitched the white thread at what angles to each other?

a) 30°

b) 60°

c) 90°

d) 60°

Ans. (i) In the kite two diagonal intersect each other at the right angle, so Raman will stitch white threads to each other with the subtention of 90°, therefore the answer is c)

(ii) Which is the correct similarity criteria applicable for smaller triangles at the upper part of this kite?

a) RHS

b) AAA

c) SSA

d) AAS

Ans.  The upper part of the kite contains two smaller triangles formed by the intersection of two diagonal at 90°  in such a way that longer diagonal bisects smaller diagonal, sides of both of the smaller triangles are equal, therefore the correct similarity criteria applicable for smaller triangles at the upper part of this kite is RHS.So, the answer is a) RHS.

(iii) Sides of two similar triangles are in the ratio 2:9. The corresponding attitudes of these triangles are in the ratio.

a) 2:3

b) 2:9

c) 81:16

d) 16:81

Ans. b) 2:9.The ratio between sides of a similar triangle is = Ratio between altitudes of the triangles = 2 : 9

(iv) Triangles switched at the tail of the kite are congruent to each other and are similar to the lower part of the kite in the ratio 2:9. If one side if the smaller triangle is of 4 cm, then the corresponding side of the kite’s lower triangle will be

a) 12 cm

b) 15 cm

c) 18 cm

d) 8 cm

 

(v) What is the area of the kite formed by the two perpendicular strings of length 8 and 12 cm?

a) 48 cm²

b) 14 cm²

c) 24 cm²

d) 96 cm²

Q18. Karma went to the lab near his home for the covid 19 test along with his family members. The seats in the waiting area were as per the norms of distancing during this pandemic (as shown in the above figure). His family member took their seats surrounded by red circular areas.

(i) Considering A as the origin, what are the coordinates of A

a) (0,1)     b) (1,0)     c) (0,0)      d) (-1,-1)

Ans. c) (0,0)

(ii) What is the distance between Neetu and Karan?

a) 10 units     b) 2√5 units     c) √10 units      d) √8 units

Ans. The coordinates of  Neetu and Karan are (3,6) and (6,5)

The distance between Neetu and Karan  is =√[(3-6)² +(6-5)²]= √10

(iii) What are the coordinates of  seat of Akash?

a) (2,3)         b) (3,2)        c) (0,3)      d) (2,0)

Ans.a) (2,3)

(iv) What will be the coordinates of a point exactly between Akash and  Binu where a person can be seated?

(a) (3.5, 2.5)         (b) (2.5, 5)         (c) (10, 5)         (d) (1.5, 0.5)

Ans.The coordinates  of Akash and  Binu are (2,3) and (5,2)

The coordinates of the point between  Akash and  Binu are

= [(2+5)/2,(3+2)/2] =(3.5,2.5)

Hence answer is (a) (3.5, 2.5)

Q19. An engineer plans to make all the pillars of the metro green with plants to contribute to a healthy environment as shown in the picture. Observe the picture and answer the questions if the dimension of one pillar is 1.5 m × 1.5 m × 20 m.

(i) The shape of the pillars is

(a) Rectangle         (b) Cube         (c) Cuboid         (d) Cylinder

Ans.  (c) Cuboid

(ii) By using which formula he can calculate the surface area of the pillar?

(a) A = 2(lb + bh + hl)         (b) A = 2(lb + hl)         (c) A = 2h(l + b)         (d) A = lb + bh + hl

Ans.A = 2h(l + b)

(iii) The lateral surface area of one pillar is

(a) 100m²         (b) 120m²         (c) 165m²         (d) 82.5m²

Ans. The lateral surace area of the  pillar is

= 2h(l+b) = 2×20(1.5+1.5) =40 ×3 = 120 cm²

(iv) How much cement is used to fill the pillar?

(a) 44m³         (b) 45m³         (c) 450m³         (d) 440m³

Ans. Volume of pillar = l ×b×h  = 1.5 ×1.5  ×20 =45 cm³

Hence answer is (c) 450m³

(v) Find the cost of the plantation if it costs Rs.50 per m²

(a) Rs.6625         (b) Rs.6000         (c) Rs.5000         (d) Rs.4100

Ans. The surface area of the  pillar  = 120 cm²

The  cost of the plantation  is  Rs.50 per m²

Therefore the cost  of plantation of the pillar is =50× 120 =  6000

Hence the answer  is  (b) Rs.6000

Q20.

A park has swings made of rubber and iron chain. Sachin who is studying in class X has noticed that this is a mathematical shape, he has learned in maths class. Following questions raised in his mind. Answer the questions by observing both pictures:

(i) Name the shape in which the wire is bent.

(a) Spiral         (b) elipse         (c) linear         (d) Parabola

Ans.  (d) Parabola

(ii) How many zeroes are there for the polynomial (shape of wire)?

(a) 2        (b) 3       (c) 1        (d) 0

Ans.(a) 2

(iii) The zeroes of the polynomial are

(a) -1, 4       (b) -1, 3        (c) 3, 5         (d) -4, 2

Ans.(a) -1, 4

(iv) What will be the expression of the polynomial?

(a) x²-3x -4       (b) x² – 2x + 3         (c) x² – 2x – 3         (d) x² + 2x + 3

Ans. The zeroes  of  the polynomial are =-1 and 4

Therefore the polynomial is

(x+1)(x -4) =x²-3x -4

Hence the answer is (a) x²-3x -4

(v) What is the value of the polynomial if x = 1?

(a) -4         (b) 5         (c) -5         (d) -6

Ans. The polynomial is  x²-3x -4

Value of polynomial at x =1 is 1²-3×1 -4   =1-3-4=1-7=-6

Hence answer is    (d) -6

Part -B

Question No.21 to 26 are very short answers type questions of 2 marks each.

Q21.Find the value of a if the distance between the points (-3,-14) and B(a,-5) is 9 units.

Ans. The distance between two points (x₁,y₁) and (x_2,y₂) is given by

We are given the distance between the points (-3,-14) and B(a,-5) is 9 units.

a² +6a +9 +81 = 81

a² +6a +9 =  0

a² +3a+3a + 9 =0

a(a +3) +3(a  +3) = 0

(a + 3)(a +3) = 0

a = ±3

Hence the value of a is ±3

OR

Find a relation between x and y such that the point (x,y) is equidistant from the point (3,6) and (-3,4).

Ans. According to question

The distance between (x,y) and (3,6) = The distance between (x,y) and (-3,4)

Applying the distance formula

x² + 9 -6x +  y² +36 -12y = x² +9 +6x  + y²  +16 -8y -6x

-6x +36 -12y  =16 -8y

-6x +36-16= -8y +12y

4y = 20 -6x

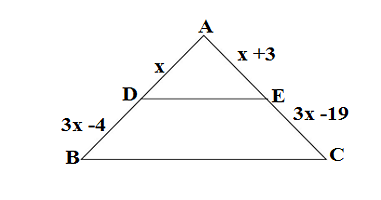
Q22. In the given figure DE||BC, find the value of x. 

In ΔABC,  DE||BC

Applying BPT theorem

x(3x -19) = (x  +3)(3x  -4)

3x² -19x = 3x² -4x +9x -12

-19x =  -4x +9x -12

24 x = 12 ⇒ x = 1/2

Q23.The sides a,b,c of a right triangle, where c is the hypotenuse, are circumscribing a circle. Prove that the radius r  of the circle is given by r = (a+b-c)/2.

Ans.

In right triangle ΔABC, AC=c, BC=a and  AB  =b

Quadrilatral DEBD will be a square ,so  DB =r

AD = b – r

AD = AF= b – r…(i)[Tangents drawn from an  external point  to the circle are equal]

BE  =  r

CE =BC-BE =a -r

CE  =CF = a -r …(ii)[Tangents drawn from an  external point  to the circle are equa]

AF = AC  – CF =c -(a -r) =c -a+ r from (ii)

b-r = c -a+ r from  (i)

2r = a + b – c

r = (a + b – c)/2, Hence proved

Q24. Draw a line segment of length 7.6 cm and divide it internally in the ratio 3: 2. Measure the two parts. 

Ans.

Steps of construction

(i) Draw a line segment AB of the length 7.6 cm.

(ii) Draw a ray AX forming an acute angle with AB.

(iii) Draw arcs on AX such that  AA₁ =A₁A₂= A₂A₃= A₃A₄ =A₄A₅

(iv) Join A₅B and draw a line A₃C||A₅B

We get AC : CB  = 3 : 2

Q25. If cos A =7/25, find the value of tan A + cot A. 

Ans. cos A =7/25 = base/hypotenuse

Perpendicur = √(25² -7²) = √(625 – 49) = √576 = 24

tan  A  = perp./base =24/7 and  cot A =base/perp. = 7/24

tan A + cot A = 24/7 + 7/24 = (576+49)/168 = 625/168

OR

If 5x = sec θ and 5/x = tan θ,then  find  the value of 5(x² – 3/x²). 

Ans. We are given 5x = sec θ ⇒ x = sec θ/5….(i)

5/x = tan θ  ⇒ 1/x =  tan θ/5……(ii)

5(x² – 3/x²)⇒ 5[(sec θ/5)²  -3×(tan θ/5)²]

= 1/5(sec² θ -3tan² θ) = 1/5(1 + tan² θ -3tan² θ)  =1/5(1 -2tan² θ)

Q26.How many terms of the AP 24,21,18……must be taken so that their sum is 78?

Ans. The given AP is 24,21,18……

Let there are n terms to make the sum 78.

Now, we have S_n= 78, a = 24, d = 21 – 24 = -3

n(48 -3n+ 3) = 156

48n -3n² +3n = 156

-3n² + 51n – 156 = 0

3n² – 51 n + 156 = 0

n² – 17 n + 52 = 0

n² – 13 n -4n + 52 = 0

n(n -13) – 4(n -13) =0

(n -13)(n -4) = 0

n = 13, 4

Therefore, either the sum of the first 13 terms or the sum of the first 4 terms of the series is 78

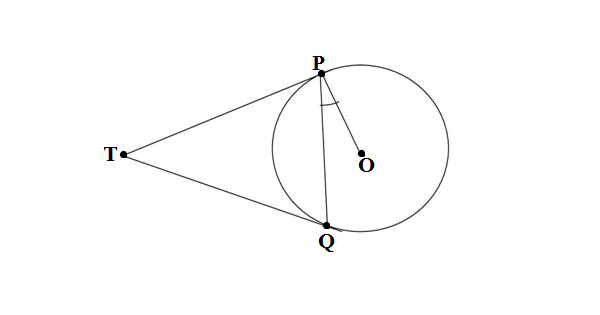
Q27.In figure two tangents  TP and TQ are drawn to a circle with centre O from an external point P. Prove that ∠PTQ = 2∠QPQ.

Ans.

Ans.

GIVEN: TP and TQ are the tangents drawn from T to the circle.

TO PROVE: ∠PTQ = 2∠QPQ

PROOF: PO is the radius of the circle

TP = TQ (tangents drawn from an external point to the circle are equal)

∠TPQ = ∠TQP (angles opposite to equal sides in a Δ)

∠OPT = 90° (angle between radius and tangent)

∠TPQ =  90°- ∠QPQ

According to the angle sum property of the Δ

∠PTQ + ∠TPQ + ∠TQP = 180°

∠PTQ + ∠TPQ + ∠TPQ = 180°

∠PTQ + 2∠TPQ = 180°

∠PTQ +2(90°- ∠QPQ) = 180°

∠PTQ + 180° – 2∠QPQ = 180°

∠PTQ = 2∠QPQ,Hence proved

Q28. Sunita has some notes of Rs.50 and Rs.100 amounting to a total of Rs.15,500. If the total number of notes is 200, then Find how many notes of Rs.50 and Rs.100 each she has?

Ans. Let the number of Rs.50 notes are x and the number of Rs.100 note are y

According to first condition of the question

50x + 100y = 15,500

x + 2y = 310…..(i)

According to second condition of the question

x + y = 200……(ii)

Subtracting equation (ii) from equation (i)

y = 110

Putting the value of y = 110 in equation (ii)

x +110 = 200

x = 200 – 110 = 90

Hence she has 90 notes of Rs 50 and 11o notes of Rs 100

Q29. Prove that √2 is an irrational number.

Ans. Let √2 is a rational number

√2 = a/b (where a and b are co-prime numbers)

b√2 = a

2b² = a²…….(i)

We get from equation (i) that a² is divisible by 2

∴ a will also be divisible by 2

Now, we can write a = 2c (where c is another positive integer)

Putting a = 2c in equation number (i)

2b² = (2c)²= 4c²

b² = 2c²……(ii)

From (ii) it is clear that b² is divisible by 2

Then b will also be divisible by 2

It is evident from equations (i) and (ii) that 2 is a common factor between a and b, so a and b can’t be co-prime. Hence our assumption for √2 as a rational number is wrong, obviously, √2 is an irrational number.

Q30. 90 cards numbered from 1 to 90 are placed in a box. If one card is drawn at random from the box find the probability that it is:

(i) a two-digit number

(ii) a perfect square

(iii) a number divisible by 5

Ans. (i) Total numbers from 1 to 90 are =90⇒Total possible O/C =90

The two digit number from 1 to 90 are =90-9 = 81, Favourable O/C =81

P(two-digit number) = Favourable O/C/Total possible O/C=81/90 =9/10

(ii) The outcomes of card drawn is of complete square number are=4,9,16,25,36,49,64,81 ⇒Favourable outcomes =8

P(a perfect square) = 8/90 = 4/45

(iii) A number divisible by 5 are =5,10,15,20,25,30,35…..90(total numbers 18)⇒ Favourable outcomes =18

P(a number divisible by 5) = 18/90 = 1/5

OR

Red Queen and a black jack are removed from a pack of 52 playing cards. Find the probability that the card drawn from the remaining cards is:

(i) a red card

(ii) neither a jack nor a king

(iii) either a king or a queen

Ans. (ii) A red queen and a black jack is removed from 52 cards then the total remaining cards are =52 -2 = 50 cards⇒Total possible outcomes =50

Total number of remaining red cards =2-1= 1⇒Favourable outcomes =1

P(a red card) =1/50

(ii) Total number of possible outcomes =50

The number of jacks and kings =3 +4 = 7

The number of cards other than jacks and king = 50 -7 = 43⇒Favourable outcomes =43

P(neither a jack nor a king) = 43/90

(iii) Total number of possible outcomes =50

The number of queens and kings =3 +4 = 7⇒Favourable outcomes =7

P(either a king or a queen) = 7/50

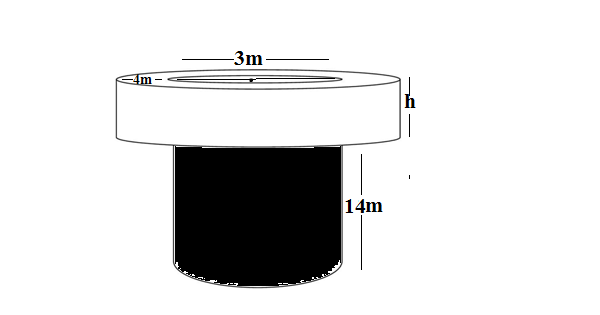
Q31. A well of diameter 3m is dug 14m deep. The earth taken out of it has been spread evenly all-around it in the shape of a circular ring of width 4m to form an embankment. Find the height of the embankment.

Ans. Let the height of the embankment is = h, the radius of the well,r =3/2=1.5 m, the width of the embankment is =4m, inner radius of the embanment,r = 1.5 m and outer radius of embankment,R = 4+1.5 = 5.5 m,depth of the well,H = 14 m

 

 

Since the embankment is created by the earth taken out from the well

Therefore, The volume of well = The volume of the embankment

πr²H = π(R²-r²)h

1.5²×14 = (5.5² -1.5²)h

(30.25-2.25)h = 31.5

28 h = 31.5

h = 31.5/28 = 1.125

Therefore,height of embankment is =1.125 m

 

Ans.  We have to prove that

Dividing numerator and denominator of LHS  by sin θ

Rearranging it

 

Multiplying numerator and denominator by the conjugate of (cot θ – cosec θ)i.e =(cot θ + cosec θ)

 

Q33. A train traveling a distance of 360 km at a uniform speed would have taken 48 minutes less to travel the same distance if its speed were 5 km/h more. Find the original speed of the train.

Ans. Let  the original speed of the train is = x  km/h

The distance traveled by train = 360 km

Time taken by the train with original speed = distance/time=360/x

If the train’s speed changed by the increase of 5 km/h, then it’s speed becomes =(x + 5) km/h.

Time taken by train with modified speed = 360/(x+5) h

48 minutes = 48/60 = 4/5 =0.8 h

According to question

360/x – 360/(x+5) = 0.8

360[1/x – 1/(x +5)] = 0.8

360[(x+5-x)/(x+5)x] =0.8

1800 = 0.8x(x+5)

0.8x² + 4x – 1800 = 0

0.2x² +x – 450 = 0

2x² +10x -4500 = 0

Applying the quadratic equation

x = (-10 +190)/4 = 180/4 = 45 or x = (-10 -190)/4 = -200/4 = -50

Since speed of the train can’t be negative,so the original speed of the train is 45 km/h.

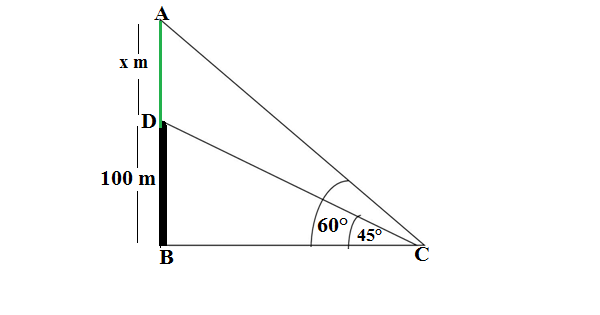
Q34. A statue which is x m tall stands on the top of a 100 m pedestal on the ground. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point, the angle of elevation of the top of the pedestal is 45°. Find the height of the statue.

Ans.

In the figure, BD is the pedestal of height 100 m and DA is the statute of the height x

 

We are given the angle of elevation of the top of the statue from a point C on the ground =60°

The angle of elevation of the top of the pedestal from the same point C =45°

tan 45° = BD/BC = 100/BC

1 = 100/BC⇒ BC = 100 m

tan 60°=AB/BC = (100 +x)/100

(100 +x)/100 = √3

100 +x = 100√3

x = 100√3 – 100 = 100(√3 – 1)

Hence, height of the statue is 100(√3 – 1) m

Q35.Find the number of terms in an AP 18,15,12……. -48 and also find the sum of all of its terms.

Ans.  Let there are n terms in the AP, the given AP is 18,15,12……. -48

The n^th term of AP is given by

a_n= a + (n-1)d, where a = 18, d = 15 -18 = -3 and a_n  = -48

18+(n-1)(-3) = -48

-3n +3 = -48 -18 = -66

-3n = -69

n = 23

Applying the following formula for getting the sum of n terms of an AP

Putting the value of n =23,a = 18, d = 15 -18 = -3

 

= 23×18 -23×66

= 414 – 1518 = -1104

Hence,sum of all terms of the given AP is -1104

Q36. Find the missing frequencies f₁  and f₂ if the mean of all observations given below is 38.2.

 

 

 

 

 

 

Ans. We are given the mean of all observations is 38.2

Arranging the table for evaluating mean of the given data

Class Interval	Frequency(f)	Class mark(x)	fx
0 – 10	4	5	20
10 – 20	4	15	60
20 -30	f1	25	25 f1
30 -40	10	35	350
40 -50	f2	45	45 f2
50 -60	8	55	440
60 -70	5	65	325
	N=50	∑fx	=1195+25 f1 +45 f2

We have

f₁+ f₂+31 = 50⇒f₁+ f₂= 19……(i)

Applying the direct method for getting the mean

25 f₁+45 f₂ =  1910- 1195

25 f₁+45 f₂= 715……(ii)

Substituting  f₁ =( 19- f₂  ) equation (i) in equation (ii)

25 ( 19- f₂  )+45 f₂= 715

475 – 25f₂  + 45 f₂= 715

20 f₂= 715 – 475 = 340

 f₂= 17

Putting the value of f₂= 17 in equation ( i)

f₁= 19-17 = 2

Hence the value of f₁ is 2 and of f₂ is 17

You can compensate us by donating any amount of money for our survival

Our Paytm NO 9891436286

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions for class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions for class 9 science 

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

NCERT Solutions for class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT Solutions for Class 10 Science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

NCERT Solutions for class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT solutions for class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals

Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2

Class 12 Maths Important Questions-Application of Integrals

Class 12 Maths Important questions on Chapter 7 Integral with Solutions for term 2 CBSE Board 2021-22

Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22

Solutions of class 12  maths question paper 2021 preboard exam CBSE Solution