Class 10 maths NCERT solutions of chapter 7- Coordinate Geometry

Class 10 maths NCERT solutions of chapter 7- Coordinate Geometry are presented here for helping the students of class 10 in their preparation of maths paper in SA-1 and SA-2 CBSE board exams. These NCERT solutions of chapter 7-Coordinate geometry will help you a complete understanding of the concept of coordinate geometry required to solve all the questions of co-ordinate geometry involved in the 10 class maths question paper of the CBSE board 2020-21. All questions of chapter 7- coordinate geometry are solved by an expert of maths as per the CBSE norms and by the step by step method so that every student could understand the solutions.

Class 10 maths NCERT solutions of chapter 7- Coordinate Geometry

Click for online shopping

Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc

EXERCISE 7.1

Q1. Find the distance between the following pairs of points:
(i) (2, 3), (4, 1)
(ii) (-5, 7), (-1, 3)
(iii) (a, b), (-a, -b

Ans. (i) Let the points are denoted by A(2, 3) and B(4, 1)

Applying the distance (d) formula between two points (x_1, y₁) and (x₂, y₂)

$\boldsymbol{d=\sqrt{(x_{1}-x_{2})^{2}+\left ( y_{1}- y_{2}\right )^{2}}}$

Here x₁ =2, y₁= 3 and x₂=4 ,y₂ = 1

$\boldsymbol{AB=\sqrt{(2-4)^{2}+\left ( 3- 1\right )^{2}}=\sqrt{\left ( -2 \right )^{2}+\left ( 2 \right )^{2}}=\sqrt{8}=2\sqrt{2}}$

(ii) A(-5, 7), B(-1, 3)

$\boldsymbol{d=\sqrt{(x_{1}-x_{2})^{2}+\left ( y_{1}- y_{2}\right )^{2}}}$

x₁ = -5, y₁= 7 and x₂= -1 ,y₂ = 3

$\boldsymbol{AB=\sqrt{(-5+1)^{2}+\left ( 7- 3\right )^{2}}=\sqrt{\left ( -4 \right )^{2}+\left ( 4 \right )^{2}}=\sqrt{32}=4\sqrt{2}}$

x₁ = a, y₁= b and x₂= -a ,y₂ = -b

$\boldsymbol{AB=\sqrt{(a+a)^{2}+\left ( b+b\right )^{2}}=\sqrt{\left ( 2a \right )^{2}+\left ( 2b \right )^{2}}=\sqrt{4a^{2}+4b^{2}}=2\sqrt{a^{2}+b^{2}}}$

Q2.Find the distance between the points (o,0) and (36,15). Can you now find the distance between the two towns A and B discussed in section 7.2.

Ans. Let the town A (0,0) and town B(36,15), so the distance (d) between two points is

$\boldsymbol{d=\sqrt{(x_{1}-x_{2})^{2}+\left ( y_{1}- y_{2}\right )^{2}}}$

x₁ = 0, y₁= 0 and x₂= 36 ,y₂ = 15

$\boldsymbol{AB=\sqrt{\left ( 0-36 \right )^{2}+\left ( 0-15 \right )^{2}}=\sqrt{36^{2}+15^{2}}=\sqrt{1296+225}=\sqrt{1521}=39}$

So, the distance between two towns A and B is = 39 units

Q3.Determine if the points (1,5), (2,3) and (-2,-11) are collinear.

Ans. Let the points are denoted by A (1,5), B(2,3) and C(-2,-11)

If the points A, B and C are collinear then they should have to satisfy the following

AB + BC = AC

The distance between A (1,5), B(2,3)

x₁ = 1, y₁= 5 and x₂= 2 ,y₂ = 3

$\boldsymbol{d=\sqrt{(x_{1}-x_{2})^{2}+\left ( y_{1}- y_{2}\right )^{2}}}$

$\boldsymbol{AB=\sqrt{\left ( 1-2 \right )^{2}+\left ( 5-3 \right )^{2}}=\sqrt{-1^{2}+2^{2}}=\sqrt{1+4}=\sqrt{5}}$

$\boldsymbol{BC=\sqrt{\left ( 2+2 \right )^{2}+\left ( 3+11 \right )^{2}}=\sqrt{4^{2}+14^{2}}=\sqrt{16+196}=\sqrt{212}}$

$\boldsymbol{AC=\sqrt{\left ( 1+2 \right )^{2}+\left ( 5+11 \right )^{2}}=\sqrt{3^{2}+16^{2}}=\sqrt{9+256}=\sqrt{265}}$

AB + BC ≠AC

Hence A, B, and C are not collinear

Q4.Check whether (5,-2), (6,4), and (7, -2) are the vertices of an isosceles triangle.

Let the vertices of the triangle are A(5,-2), B(6,4), and C(7, -2)

$\boldsymbol{AB =\sqrt{\left ( 5-6 \right )^{2}+\left ( -2-4 \right )^{2}}=\sqrt{\left ( -1 \right )^{2}+\left ( -6 \right )^{2}}=\sqrt{37}}$

$\boldsymbol{BC =\sqrt{\left ( 6-7 \right )^{2}+\left ( 4+2 \right )^{2}}=\sqrt{\left ( -1 \right )^{2}+\left ( 6 \right )^{2}}=\sqrt{37}}$

$\boldsymbol{AC =\sqrt{\left ( 5-7 \right )^{2}+\left ( -2+2 \right )^{2}}=\sqrt{\left ( -2 \right )^{2}+\left ( 0 \right )^{2}}= \sqrt{4}=2}$

AB = BC

Therefore (5,-2), (6,4), and (7, -2) are the vertices of an isosceles triangle

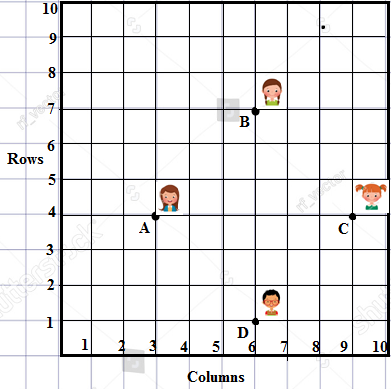
Q5. In a classroom, 4 friends are seated at points A, B, C, and D as shown in the given figure. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using distance formula, find which of them is correct.

You can see the video -Class 10 Maths NCERT solution of Question no-5 Exercise 7.1 Chapter 7 Coordinate Geometry

Ans. It is seen in the figure that the coordinates of the A, B, C and are follows

A(3,4), B(6,7), C(9,4) and D(6,1)

For checking ABCD is a square, let’s check the length of 4 sides and diagonals by applying the distance formula

$\boldsymbol{d=\sqrt{(x_{1}-x_{2})^{2}+\left ( y_{1}- y_{2}\right )^{2}}}$

$\boldsymbol{AB =\sqrt{\left ( 6-9 \right )^{2}+\left ( 7-4 \right )^{2}}=\sqrt{\left ( -3 \right )^{2}+\left ( 3 \right )^{2}}= \sqrt{9+9}=3\sqrt{2}}$

$\boldsymbol{BC =\sqrt{\left ( 6-9 \right )^{2}+\left ( 7-4 \right )^{2}}=\sqrt{\left ( -3 \right )^{2}+\left ( 3 \right )^{2}}= \sqrt{9+9}=3\sqrt{2}}$

$\boldsymbol{CD =\sqrt{\left ( 9-6 \right )^{2}+\left ( 4-1 \right )^{2}}=\sqrt{\left ( 3 \right )^{2}+\left ( 3 \right )^{2}}= \sqrt{9+9}=3\sqrt{2}}$

$\boldsymbol{AD =\sqrt{\left ( 3-6 \right )^{2}+\left ( 4-1 \right )^{2}}=\sqrt{\left (- 3 \right )^{2}+\left ( 3 \right )^{2}}= \sqrt{9+9}=3\sqrt{2}}$

So, AB = BC = CD = AD

Now the calculating length of the diagonals AC and BD

The coordinates of both ends of the diagonal AC are (3,4) and (9,4)

$\boldsymbol{AC =\sqrt{\left ( 3-9 \right )^{2}+\left ( 4-4 \right )^{2}}=\sqrt{\left (- 6 \right )^{2}+\left ( 0 \right )^{2}}= \sqrt{36}=6}$

The coordinates of both ends of the diagonal BD are (6,7) and (7,1)

$\boldsymbol{BD =\sqrt{\left ( 6-6 \right )^{2}+\left ( 7-1 \right )^{2}}=\sqrt{\left (0 \right )^{2}+\left ( 6 \right )^{2}}= \sqrt{36}=6}$

The length of both diagonals are also equal

Since all sides and diagonals of ABCD are equal, so Champa is correct that ABCD is a square.

Q6.Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer.
(i) (-1, -2), (1, 0), (-1, 2), (-3, 0)
(ii) (-3, 5), (3, 1), (0, 3), (-1, -4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2)

Ans. (i) Let the vertices of the quadrilateral are A (-1, -2), B(1, 0), C(-1, 2) and D(-3, 0)

Determining the length of the sides AB, BC, CD, AD, and diagonals AC and BD by applying the distance formula

$\boldsymbol{AB =\sqrt{\left ( -1-1 \right )^{2}+\left ( -2-0 \right )^{2}}=\sqrt{\left (-2 \right )^{2}+\left ( -2 \right )^{2}}= \sqrt{8}=2\sqrt{2}}$

$\boldsymbol{BC =\sqrt{\left ( 1+1 \right )^{2}+\left ( 0-2 \right )^{2}}=\sqrt{\left (2 \right )^{2}+\left ( -2 \right )^{2}}= \sqrt{8}=2\sqrt{2}}$

$\boldsymbol{CD =\sqrt{\left ( -1+3 \right )^{2}+\left ( 2-0 \right )^{2}}=\sqrt{\left (2 \right )^{2}+\left ( 2 \right )^{2}}= \sqrt{8}=2\sqrt{2}}$

$\boldsymbol{AD =\sqrt{\left ( -1+3 \right )^{2}+\left ( -2-0 \right )^{2}}=\sqrt{\left (2 \right )^{2}+\left ( -2 \right )^{2}}= \sqrt{8}=2\sqrt{2}}$

$\boldsymbol{AC =\sqrt{\left ( -1+1 \right )^{2}+\left ( -2-2 \right )^{2}}=\sqrt{\left (0 \right )^{2}+\left ( -4 \right )^{2}}= \sqrt{16}=4}$

$\boldsymbol{BD =\sqrt{\left ( 1+3 \right )^{2}+\left ( 0-0 \right )^{2}}=\sqrt{\left (4 \right )^{2}+\left ( 0 \right )^{2}}= \sqrt{16}=4}$

The length of all sides AB = BC = CD = AD = 2√2 and length of diagonals AC = BD = 4,therefore ABCD is a square.

(i) Let the vertices of the quadrilateral are A (-3, 5), B(3, 1), C(0, 3) and D(-1, -4)

Determining the length of the sides AB, BC, CD, AD by applying the distance formula

$\boldsymbol{AB =\sqrt{\left ( -3-3 \right )^{2}+\left ( 5-1 \right )^{2}}=\sqrt{\left (-6 \right )^{2}+\left ( 4 \right )^{2}}= \sqrt{52}=2\sqrt{13}}$

$\boldsymbol{BC =\sqrt{\left ( 3-0 \right )^{2}+\left ( 1-3 \right )^{2}}=\sqrt{\left (3 \right )^{2}+\left ( -2 \right )^{2}}= \sqrt{13}}$

$\boldsymbol{CD =\sqrt{\left ( 0+1 \right )^{2}+\left ( 3+4 \right )^{2}}=\sqrt{\left (1 \right )^{2}+\left ( 7 \right )^{2}}= \sqrt{50}}$

$\boldsymbol{AD =\sqrt{\left ( -3+1 \right )^{2}+\left ( 5+4 \right )^{2}}=\sqrt{\left (-2 \right )^{2}+\left ( 9 \right )^{2}}= \sqrt{85}}$

All sides are not equal, therefore the given points are vertices of a simple quadrilateral

(iii) Let the vertices of the quadrilateral are A(4, 5), B(7, 6), C(4, 3), D(1, 2)

Determining the length of the sides AB, BC, CD, AD by applying the distance formula

$\boldsymbol{AB =\sqrt{\left ( 4-7 \right )^{2}+\left ( 5-6 \right )^{2}}=\sqrt{\left (-3 \right )^{2}+\left ( -1 \right )^{2}}= \sqrt{10}}$

$\boldsymbol{BC =\sqrt{\left ( 7-4 \right )^{2}+\left ( 6-3 \right )^{2}}=\sqrt{\left (3 \right )^{2}+\left ( 3 \right )^{2}}= 3\sqrt{2}}$

$\boldsymbol{CD =\sqrt{\left ( 4-1 \right )^{2}+\left ( 3-2 \right )^{2}}=\sqrt{\left (3 \right )^{2}+\left ( 1 \right )^{2}}= \sqrt{10}}$

$\boldsymbol{AD =\sqrt{\left ( 4-1 \right )^{2}+\left ( 5-2 \right )^{2}}=\sqrt{\left (3 \right )^{2}+\left ( 3 \right )^{2}}= 3\sqrt{2}}$

AB = CD = √10 and BC = AD = 3√2

Opposites sides of the quadrilateral are equal therefore ABCD is a parallelogram

Q7. Find the point on the x-axis which is equidistant from (2, -5) and (-2, 9).

You can see the Video also

Ans. Let the point on the x-axis is A(x, 0) which is equidistant from B(2, -5) and C(-2, 9)

∴ AB = AC

The distance between A(x,0) and B(2, -5) = The distance between A(x,0) and C(-2, 9)

$\boldsymbol{\sqrt{\left ( x-2 \right )^{2}+\left ( 0+5 \right )^{2}}=\sqrt{\left ( x+2 \right )^{2}+\left ( 0-9 \right )^{2}}}$

$\boldsymbol{\boldsymbol{}\sqrt{x^{2}+4-4x+25}=\sqrt{x^{2}+4+4x+81}}$

x² – 4x +29 = x ² + 4x + 85

8x = – 5 6

x = -7

Hence the point on the x-axis is A(-7, 0) which is equidistant from B(2, -5) and C(-2, 9)

Q8. Find the values of y for which the distance between the points P (2, -3) and Q (10, y) is 10 units.

Ans. The distance between the points P (2, -3) and Q (10, y) = 10 units

$\boldsymbol{\sqrt{\left ( 2-10 \right )^{2}+\left ( -3-y \right )^{2}}=10}$

$\boldsymbol{\sqrt{\left ( -8 \right )^{2}+9+y^{2}+6y}=10}$

64 + 9 + y² + 6y = 100

y² + 6y – 27 = 0

y² + 9y – 3y – 27 = 0

y(y + 9) – 3( y + 9) = 0

(y + 9)( y – 3) = 0

y = -9, y = 3

Hence the required value of y is – 9 or 3

Q9. If Q (0, 1) is equidistant from P (5, -3), and R (x, 6), find the values of x. Also, find the distances QR and PR.

Ans. We are given that Q (0, 1) is equidistant from P (5, -3), and R (x, 6)

The distance between Q(0,1) and P(5, -3) = The distance between Q(0,1) and R(x, 6)

$\boldsymbol{\sqrt{\left ( 0-5 \right )^{2}+\left ( 1+3 \right )^{2}}=\sqrt{\left ( 0-x \right )^{2}+\left ( 1-6 \right )^{2}}}$

25 +16 = x² + 25

x = ± 4

The coordinates of Q are (0,1) and of R are ( ± 4, 6)

$\boldsymbol{QR= \sqrt{\left ( 0\pm 4 \right )^{2}+\left ( 1-6 \right )^{2}}=\sqrt{16+25}=\sqrt{41}}$

The coordinates of P are (5,-3) and of R are ( ± 4, 6)

Taking P(5, -3) and R( 4, 6)

$\boldsymbol{PR= \sqrt{\left ( 5- 4 \right )^{2}+\left ( -3-6 \right )^{2}}=\sqrt{1+81}=\sqrt{82}}$

Taking P(5, -3) and R( -4, 6)

$\boldsymbol{PR= \sqrt{\left ( 5+ 4 \right )^{2}+\left ( -3-6 \right )^{2}}=\sqrt{81+81}=\sqrt{162}=9\sqrt{2}}$

Therefore QR = √41 and PR = √82, 9√2

Q10.Find a relation between x and y such that the point (x, y) is equidistant from the points (3, 6) and (-3, 4).

Ans. It is given to us that the point (x, y) is equidistant from the points (3, 6) and (-3, 4)

The distance between (x.y) and (3,6) = The distance between (x,y) and (-3,4)

$\boldsymbol{\sqrt{\left ( x- 3\right )^{2}+\left ( y-6 \right )^{2}}=\sqrt{\left ( x+3 \right )^{2}+\left ( y-4 \right )^{2}}}$

Squaring both sides

(x – 3)² + ( y – 6)² = (x + 3)² + ( y – 4)²

x² + 9 – 6x + y² + 36 – 12y = x² + 9 + 6x + y² + 16 – 8y

– 6x – 6x – 12y + 8y + 45 – 25 = 0

– 12x – 4y + 20 = 0

–4(3x + y – 5) = 0

3x + y – 5 = 0

Hence required relationship between x and y is 3x + y – 5 = 0

Class 10 maths NCERT solutions of chapter 7- Coordinate Geometry

EXERCISE 7.2

Q1. Find the coordinates of the point which divides the join of (- 1, 7) and (4, – 3) in the ratio 2:3.

Ans. Let the coordinates of the point C are (x,y) which divides the join of (- 1, 7) and (4, – 3)

You can see the video -Class 10 Maths NCERT solution of Question no-1 Exercise 7.2 Chapter 7 Coordinate Geometry

Applying the section formula

$\boldsymbol{x =\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}}, y=\frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}}}$

x₁ = –1, y₁= 7 , x₂= 4, y₂= – 3, m₁ = 2, m₂ = 3

$\boldsymbol{x=\frac{2\times 4+3\times -1}{2+3}, y = \frac{2\times -3+3\times 7}{2+3}}$

$\boldsymbol{x=\frac{8-3}{5},y=\frac{-6+21}{5}}$

x = 1, y =3

Hence the coordinates of C are (1,3)

Q2.Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).
Solution:

Ans. Let P(a,b) and Q(c,d) trisect the line segment joining A(4, -1) and B(-2, -3)

Applying the section formula for coordinates of P(a,b) that divides the given line segment in 1 : 2

$\boldsymbol{x =\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}}, y=\frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}}}$

x₁ = 4, y₁= -1, x₂= -2, y₂= – 3, m₁ = 1, m₂ = 2 and (x,y) = (a, b)

$\boldsymbol{a = \frac{1\times -2+2\times 4}{1+2}, b=\frac{1\times -3+2\times -1}{1+2}}$

$\boldsymbol{a=\frac{-2+8}{3},b=\frac{-3-2}{3}}$

a = 2, b = –5/3, Coordinates of P are ( 2, -5/3)

Co-ordinates of Q are 1/2(2 -2),1/2[(-5/3)-3] =(0,-10/3)

Q3.(c,d) is the mid points of the line segment joing P(a,b) and B(-2,-3), (a,b) = (2, -5/3)

$\boldsymbol{c=\frac{2-2}{2},d=\frac{-3-5/3}{2}}$

c = 0, d = -7/3

So, coordinates of Q are (0, -7/3)

Hence the points P(2, -5/3) and Q(0. -7/3) trisects the line segment AB.

Q3.To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1 m each. 100 flower pots have been placed at a distance of 1 m from each other along with AD, as shown in the following figure. Niharika runs 1/4 th the distance AD on the 2nd line and posts a green flag. Preet runs 1/5th the distance AD on the eighth line and posts a red flag. What is the distance between both the flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag?

Ans. We are given distance AD = 100 m and 100 flower pots which are placed at a distance of 1 m.

Niharika placed the flag on the second line at a distance of

$\boldsymbol{=\frac{1}{4}\: of\: 100=25}$

Niharika placed the flag at a distance of 25 m from the starting point means on the line of 25 th flower pot, so the coordinates of the point Niharika placed the flag are (2, 25)

Preet placed the flag on the eighth line at a distance of

$\boldsymbol{=\frac{1}{5}\: of\: 100=20}$

Niharika placed the flag at a distance of 20 m from the starting point means on the line of 20 th flower pot, so the coordinates of the point Niharika placed the flag are (8, 20)

The distance between both of the flags located at(2,25) and (8,20) is

$\boldsymbol{=\sqrt{\left ( 2-8 \right )^{2}+\left ( 25-20 \right )^{2}}=\sqrt{\left ( -6 \right )^{2}+5^{2}}=\sqrt{36+25}=\sqrt{61}}$

So, the distance between both of the flags is √61 m.

Rashmi placed the flag at the midpoint of both of these flags located at (2, 25) and (8, 20), let the coordinates of the point at which Rashmi posted the flag are (x, y).

$\boldsymbol{x=\frac{2+8}{2}, y =\frac{25+20}{2}}$

$\boldsymbol{x=5, y =22.5}$

Rashmi placed her blue flag on 5 th line at a distance of 22.5 m.

Q4.Find the ratio in which the line segment joining the points (-3, 10) and (6, – 8) is divided by (-1, 6).

Ans. Applying the section formula

$\boldsymbol{x =\frac{kx_{2}+x_{1}}{k+1},y =\frac{ky_{2}+y_{1}}{k+1}}$

x₁ = -3, y₁= 10 and x₂= 6 ,y₂ = -8, x = -1, y = 6 and k= m₁/m₂ where (m₁ : m₂) is the ratio at which (-1, 6) point divides the line segment

$\boldsymbol{-1 =\frac{6k-3}{k+1},6 =\frac{-8k+10}{k+1}}$

-k -1 = 6k – 3, 6k + 6 = -8k + 10

-7k = -2, 14 k = 4

k = 2/7, k = 2/7

Both of the equation confirms that the point (-1, 6) divides the line segment in 2 : 7.

Q5. Find the ratio in which the line segment joining A (1, – 5) and B (- 4, 5) is divided by the x-axis. Also find the coordinates of the point of division.

Ans. Let the point on x-axis at which the line segment joining A (1, – 5) and B (- 4, 5) is divided by the x-axis is = (x, 0)

We are having the known value of y coordinate of (x,0) = 0, so applying the section formula accordingly.

$\boldsymbol{y=\frac{ky_{2}+y_{1}}{k+1}}$

y₁= -5 , y₂ = 5, y = 0

$\boldsymbol{0=\frac{5k-5}{k+1}}$

5k – 5 = 0

k = 1

Hence the ratio at which the line segment is divided by x axis is 1 : 1.

Let the coordinates of the point of division are (x,y)

$\boldsymbol{x =\frac{kx_{2}+x_{1}}{k+1},y =\frac{ky_{2}+y_{1}}{k+1}}$

x₁ = 1, y₁= -5 and x₂= -4 ,y₂ = 5, (x , y) = (x,0), k = 1

$\boldsymbol{x=\frac{-4\times 1+1}{1+1}=\frac{-4+1}{2}=\frac{-3}{2}}$

Hence the coordinates of point of division are (-3/2, 0)

Q6. If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.

Ans. Let the vertices of a parallelogram are A(1, 2), B(4, y), C(x, 6) and D(3, 5)

Since the diagonals of a parallelogram bisect each other

The midpoint of AC = Midpoint of BD

$\boldsymbol{\left ( \frac{1+x}{2},\frac{2+6}{2} \right )=\left ( \frac{4+3}{2},\frac{y+5}{2} \right )}$

$\boldsymbol{\frac{1+x}{2}=\frac{4+3}{2}=\frac{7}{2}}$

x = 6

$\boldsymbol{\frac{y+5}{2}=\frac{2+6}{2}=4}$

y = 3

Hence the value of x = 6 and of y = 3

Q7.Find the coordinates of point A, where AB is the diameter of a circle whose centre is (2, – 3) and B is (1,4).

Ans. AB is the diameter of the circle and the coordinates of B and of centre are given (1,4) and (2, -3) respectively.

Let the coordinates of another end(A) of diameter is = (x, y)

(2, -3) is the centre of circle so it is the midpoint of AB

$\boldsymbol{\left (2,-3 \right )=\left ( \frac{1+x}{2},\frac{4+y}{2} \right )}$

$\boldsymbol{\frac{1+x}{2}=2}$

x = 3

$\boldsymbol{\frac{4+y}{2}=-3}$

y = -6 – 4 = -10

Hence the coordinates of A are (3, -10)

Q8. If A and B are (-2, -2) and (2, -4), respectively, find the coordinates of P such that AP = 3/7 AB and P lies on the line segment AB.

Ans.

We are given that

$\boldsymbol{AP= \frac{3}{7}AB}$

$\boldsymbol{\frac{AP}{AB}=\frac{3}{7}}$

$\boldsymbol{\frac{AB}{AP}=\frac{7}{3}}$

Subtracting 1 from both sides

$\boldsymbol{\frac{AB}{AP}-1=\frac{7}{3}-1}$

$\boldsymbol{\frac{AB-AP}{AP}=\frac{7-3}{3}=\frac{4}{3}}$

AB – AP = BP

$\boldsymbol{\frac{BP}{AP}=\frac{4}{3}}$

AP: BP = 3 : 4

Coordinates of both ends of line segments are A(-2,-2) and B(2, -4) . Let coordinates of P are (x, y) that divides AB in 3 : 4.

Applying the section formula

$\boldsymbol{x =\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}}, y=\frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}}}$

x₁ = -2, y₁= -2 and x₂= 2 ,y₂ = -4, ,m₁ = 3, m₂ = 4

$\boldsymbol{x=\frac{2\times 3-2\times 4}{3+4},y =\frac{-4\times 3-2\times 4}{3+4}}$

$\boldsymbol{x=\frac{-2}{7}, y =\frac{-20}{7}}$

Hence the coordinates of P are (-2/7, -20/7)

Q9.Find the coordinates of the points which divide the line segment joining A (- 2, 2) and B (2, 8) into four equal parts.

Ans.Drawing a line segment AB in which P, Q and R points divide it into four equal parts

It is seen in the figure that P , Q, and R divides AB in the ratio of 1 : 3, 1: 1 and 3: 1 respectively

For calculating the coordinates of P (x,y) , applying section formula

$\boldsymbol{x =\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}}, y=\frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}}}$

x₁ = -2, y₁= 2 and x₂= 2 ,y₂ = 8, ,m₁ = 1, m₂ = 3

$\boldsymbol{x=\frac{1\times 2+3\times -2}{1+3}, y= \frac{1\times 8+3\times 2}{1+3}}$

x = -1, y = 7/2

So, coordinates of P are (-1, 7/2)

Q is the midpoint of AB, the coordinates of A and B are (-2,2) and (2,8)

So, coordinates of Q = 1/2(-2 +2), 1/2(2 + 8)= (0,5)

R is the mid point of BQ, the coordinates of B and Q are (2. 8) and (0,5)

So, coordinates of R = 1/2(2 +0), 1/2(8 + 5) = (1, 13/2)

Hence the coordinates of P, Q and R are (-1, 7/2), (0,5) and (1, 13/2) respectively

Q10.Find the area of a rhombus if its vertices are (3, 0), (4, 5), (-1, 4) and (-2,-1) taken in order.

[Hint: Area of a rhombus = 1/2(product of its diagonals)]

Ans. Let the vertices of the rhombus are A(3,0), B(4,5), C(-1,4) and D(-2, -1) respectively

Area of rhombus = 1/2(Product of diagonals)

So, let’s found out the length of the diagonals AC and BD by applying the distance formula

$\boldsymbol{AC=\sqrt{\left ( 3+1 \right )^{2}+\left ( 0-4 \right )^{2}}=\sqrt{4^{2}+\left ( -4 \right )^{2}}=\sqrt{32}=4\sqrt{2}}$

$\boldsymbol{BD=\sqrt{\left ( 4+2 \right )^{2}+\left ( 5+1 \right )^{2}}=\sqrt{6^{2}+\left ( 6 \right )^{2}}=\sqrt{32}=6\sqrt{2}}$

Area of rhombus ABCD = 1/2(AC× BD) = 1/2( 4√2 × 6√2) = 1/2(24 × 2) = 24 Sq.unit

Class 10 maths NCERT solutions of chapter 7- Coordinate Geometry

EXERCISE 7.3

Q1. Find the area of the triangle whose vertices are:

(i) (2, 3), (-1, 0), (2, -4)

(ii) (-5, -1), (3, -5), (5, 2)

Ans. Area of Δ

$=\frac{1}{2}(x_{1}(y_{2}-y_{3})+(x_{2}(y_{3}-y_{1})\textup{}+(x_{3}(y_{1}-y_{2}))$

(i) Let vertices of the triangles are A(2, 3), B(-1, 0) and C(2, -4)

x₁ = 2, y₁ = 3, x₂= -1, y₂ = 0, x₃ = 2, y₃ = – 4

Substitute all the values in the above formula, we get

Area of Δ

$\boldsymbol{\boldsymbol{}ar\Delta ABC=\frac{1}{2}\left [ 2\left ( 0+4 \right )-1\left ( -4-3 \right )+2\left ( 3-0 \right ) \right ]}$

$\boldsymbol{\boldsymbol{}=\frac{1}{2}\left [ 8+7+6 \right ]=\frac{21}{2}=10.5}$

Therefore area of the triangle is = 10.5 sq.unit

(ii) Let vertices of the triangles are A(-5, -1) , B (3, -5) and C(5, 2)

x₁ = -5, y₁ = -1, x₂= 3, y₂ = -5, x₃ = 5, y₃ = 2

$\boldsymbol{ar\Delta ABC=\frac{1}{2}\left [ -5\left ( -5-2 \right )+3\left ( 2+1 \right )+5\left ( -1+5 \right ) \right ]}$

$\boldsymbol{=\frac{1}{2}\left ( 35+9+20 \right )=\frac{64}{2}=32}$

Therefore area of triangle is = 32 sq.unit

Q2. In each of the following find the value of ‘k’, for which the points are collinear.

(i) (7, -2), (5, 1), (3, -k)

(ii) (8, 1), (k, -4), (2, -5)

Ans. The points will be collinear if the area formed by these points is zero, since the figure formed by the three points must be a triangle, so applying the formula of triangle.

$\boldsymbol{ar \: of\: \Delta= \frac{1}{2}\left [ x_{1}\left ( y_{2}-y_{3} \right )+x_{2}\left ( y_{3}-y_{1}) +x_{3}\left ( y_{1}-y_{2} \right )\right ) \right ]}$

(i) x₁ = 7, y₁ = -2, x₂= 5, y₂ = 1, x₃ = 3, y₃ = -k

$\boldsymbol{\frac{1}{2}\left [ 7\left ( 1+k \right )+5\left ( -k+2) +3\left ( -2-1 \right )\right ) \right ]=0}$

7(1 +k) + 5(-k + 2) + 3( -2 -1) = 0

7k -5k + 7 + 10 – 9 = 0

2k + 8 = 0

k = – 4

(ii) The points will be collinear if the area of the triangle formed by the points (8, 1), (k, -4), (2, -5) is zero.

x₁ = 8, y₁ = 1, x₂= k, y₂ = -4, x₃ = 2, y₃ = -5

$\boldsymbol{ \frac{1}{2}\left [ 8\left ( -4+ 5 \right )+k\left ( -5-1) +2\left ( 1+4 \right )\right ) \right ]=0}$

8 – 6k +10 = 0

-6k = -18

k = 3

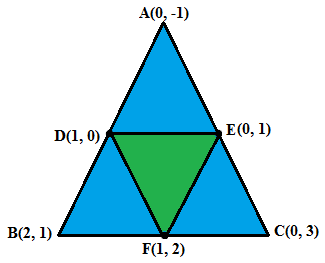
Q3.Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.

Ans. Let the verteces of the triangle are A(0, -1), B (2, 1) and C(0, 3)

The cordinates of A and B are (0, -1) and (2, 1)

So, the mid point of AB = 1/2(0 + 2)/2, 1/2(-1 + 1)/2 = D(1, 0)

The cordinates of B and C are (2, 1) and (0, 3)

So,the mid point of BC are = 1/2(2+0), 1/2(1 +3) = F(1 , 2)

The cordinates of A and C are (0, -1) and (0, 3)

So,the mid point of AC are = 1/2(0 +0), 1/2(-1 +3) = E(0 , 1)

The vertices of the ΔABC are (0, -1), (2, 1) and (0, 3)

$\boldsymbol{ar \: of\: \Delta= \frac{1}{2}\left [ x_{1}\left ( y_{2}-y_{3} \right )+x_{2}\left ( y_{3}-y_{1}) +x_{3}\left ( y_{1}-y_{2} \right )\right ) \right ]}$

x₁ = 0, y₁ = -1, x₂= 2, y₂ = 1, x₃ = 0, y₃ = 3

$\boldsymbol{ ar\Delta ABC=\frac{1}{2}\left [ 0\left ( 1-0 \right )+2\left ( 3+1) +0\left ( -1-1 \right )\right ) \right ]}$

arΔABC = 4 sq.unit

The vertices of the ΔDEF are (1, 0), (0, 1) and (1, 2)

x₁ = 1, y₁ = 0, x₂= 0, y₂ = 1, x₃ = 1, y₃ = 2

$\boldsymbol{ ar\Delta DEF=\frac{1}{2}\left [ 1\left ( 1-2 \right )+0\left ( 2-0) +1\left ( 0-1 \right )\right ) \right ]}$

arΔDEF = -1 , avoiding minus sign because area can’t be negative

arΔDEF = 1 square unit

The ratio of ΔDEF to ΔABC

$\boldsymbol{\frac{ar\Delta DEF}{ar\Delta ABC}=\frac{1}{4}}$

Therefore the required ratio of both triagles is 1 : 4

Q4.Find the area of the quadrilateral whose vertices, taken in order, are

(-4, -2), (-3, -5), (3, -2) and (2, 3).

Ans. Let the vertices of quadrilatral are A(-4, -2), B(-3, -5), C(3, -2) and D(2, 3)

After we draw a diagonal AC, we get two triangles ΔABC and ΔADC

The triangle ABC has the vertices ( -4, -2), (-3, -5) and (3, -2 )

$\boldsymbol{ar \: of\: \Delta= \frac{1}{2}\left [ x_{1}\left ( y_{2}-y_{3} \right )+x_{2}\left ( y_{3}-y_{1}) +x_{3}\left ( y_{1}-y_{2} \right )\right ) \right ]}$

x₁ = -4, y₁ = -2, x₂= -3, y₂ = -5, x₃ = 3, y₃ = -2

$\boldsymbol{ar\Delta ABC=\frac{1}{2}\left [ -4\left ( -5+2 \right )-3\left ( -2+2 \right )+3\left ( -2+5 \right ) \right ]}$

$\boldsymbol{=\frac{1}{2}\left [ 12 +0+9 \right ]=\frac{21}{2}=10.5}$

So, area of ABC is = 10.5 sq.unit

The triangle ADC has the vertices ( -4, -2), (2, 3) and (3, -2 )

x₁ = -4, y₁ = -2, x₂= 2, y₂ = 3, x₃ = 3, y₃ = -2

$\boldsymbol{ar\Delta ADC=\frac{1}{2}\left [ -4\left ( 3+2 \right )+2\left ( -2+2 \right )+3\left ( -2-3 \right ) \right ]}$

$\boldsymbol{=\frac{1}{2}\left [ -20 +0-15 \right ]=\frac{-35}{2}}$

Avoiding minus sign because area can’t be negative

arΔADC = 35/2 = 17.5 sq,unit

Area of given quadrilateral ABCD = ar ΔABC + ar ΔADC = 10.5 + 17.5 = 28 sq.unit

Q5.You have studied in Class IX that a median of a triangle divides it into two triangles of equal areas. Verify this result for ΔABC whose vertices are A (4, – 6), B (3, – 2) and C (5, 2).

Ans. We are given the vertices of the triangle A (4, – 6), B (3, – 2) and C (5, 2)

Let CD is the mediun of the triagle ABC, so D is the mid point of AB

The coordinates of D are = 1/2(4 +3), 1/2(-6 -2) = (7/2, -4)

We have to show the area of triagle ADC = area of triagle DBC

The verteces of the triagle ADC are (4, -6), (5, 2), C(7/2, -4)

$\boldsymbol{ar \: of\: \Delta= \frac{1}{2}\left [ x_{1}\left ( y_{2}-y_{3} \right )+x_{2}\left ( y_{3}-y_{1}) +x_{3}\left ( y_{1}-y_{2} \right )\right ) \right ]}$

x₁ = 4, y₁ = -6, x₂= 5, y₂ = 2, x₃ = 7/2, y₃ = -4

$\boldsymbol{ar\Delta ADC=\frac{1}{2}\left [ 4\left ( 2+4 \right )+5\left ( -4+6 \right ) +\frac{7}{2}\left ( -6-2 \right )\right ]}$

$\boldsymbol{=\frac{1}{2}\left [ 24+10-28 \right ]=\frac{6}{2}=3}$

Area of triagle

The vertices of the triangle DBC are (7/2, -4), (3, -2), C(5, 2)

x₁ = 7/2, y₁ = -4, x₂= 3, y₂ = -2, x₃ = 5, y₃ = 2

$\boldsymbol{ar\Delta DBC=\frac{1}{2}\left [ \frac{7}{2}\left ( -2-2 \right )+3\left ( 2+4 \right )+5\left ( -4+2 \right ) \right ]}$

$\boldsymbol{=\frac{1}{2}\left [ -14+18-10 \right ]=\frac{-6}{2}=-3}$

Avoiding minus sign because area can’t be negative

So, area of triangle DBC = 3 sq.unit

Hence area of ADC = area of DBC

Therefore mediun CD divides the triangle ABC into two equal parts.

Class 10 maths NCERT solutions of chapter 7- Coordinate Geometry

Exercise 7.4

Q1. Determine the ratio in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, –2) and B(3, 7).

Ans. Let the given line divides the line segment in the ratio of (m₁ : m₂) and the point of intersection is x, y

$\boldsymbol{x=\frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}}, y=\frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}}}$

x₁ = 2, x₂= 3, y₁ = -2, y₂ = 7

$\boldsymbol{x=\frac{3m_{1}+ 2m_{2}}{m_{1}+m_{2}}, y=\frac{7m_{1}-2m_{2}}{m_{1}+m_{2}}}$

Since the line 2x + y – 4 = 0 passes through the poins(x, y), so the coordinates will satisfy the equation.

$\boldsymbol{2\left ( \frac{3m_{1}+2m_{2}}{m_{1}+m_{2}} \right )+\frac{7m_{1}-2m_{2}}{m_{1}+m_{2}}-4=0}$

$\boldsymbol{6m_{1}+4m_{2}+7m_{1}-2m_{2}-4m_{1}-4m_{2}=0}$

$\boldsymbol{9m_{1}-2m_{2}=0}$

$\boldsymbol{\frac{m_{1}}{m_{2}}=\frac{2}{9}}$

Therefore the given line divides the line segment in 2 : 9

Q2. Find the relation between x and y if the points (x, y), (1, 2) and (7, 0) are collinear.

Ans. If the given points are collinear then the area of the triangle formed by these points must be zero

$\boldsymbol{ar\Delta =\frac{1}{2}\left [ x_{1}\left ( y_{2}-y_{3} \right )+x_{2}\left ( y_{3}-y_{1} \right )+x_{3}\left ( y_{1}-y_{2} \right ) \right ]}$

x₁ = x, x₂= 1, y₁ = y, y₂ = 2, x₃ = 7, y₃ = 0

$\boldsymbol{0 =\frac{1}{2}\left [ x\left ( 2-0 \right )+1\left ( 0-y \right )+7\left ( y-2 \right ) \right ]}$

2x – y + 7y -14 = 0

2x + 6y = 14

x + 3y = 7

Therefore the required relationship between x and y is x + 3y = 7

Q3. Find the centre of a circle passing through points (6, -6), (3, -7) and (3, 3).

Ans. Let the centre of circle is (x, y), the distance of the centre to the circle is known as radii

So, the distance between (x,y) and (6, -6) = The distance between (x,y) and (3, -7)

$\boldsymbol{\sqrt{\left ( x-6 \right )^{2}+\left ( y+6 \right )^{2}}=\sqrt{\left ( x-3 \right )^{2}+\left ( y+7 \right )^{2}}}$

x² + 6² – 12x + y² + 6² + 12x = x² + 3² – 6x + y² + 7² + 14y

72 = -6x + 14y + 9 + 49

6x – 14y + 14 = 0

3x – 7y + 7 = 0…….(i)

The distance between (x,y) and (6, -6) = The distance between (x,y) and (3, 3)

$\boldsymbol{\sqrt{\left ( x-6 \right )^{2}+\left ( y+6 \right )^{2}}=\sqrt{\left ( x-3 \right )^{2}+\left ( y-3 \right )^{2}}}$

x² + 6² – 12x + y² + 6² + 12x = x² + 3² – 6x + y² + 3² – 6y

72 = -6x – 6y + 18

6x + 6y + 54 = 0

x + y + 9 = 0…….(ii)

Multiplying eq. by 3 , we get eq.(iii)

3x + 3y + 27 = 0……(iii)

Subtracting eq.(i) from (iii)

10y + 20 = 0

y = -2

Putting the value of y = -2 in eq.(1)

x = 3

Therefore coordinates of the centre of the circle is (3, -2)

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions for class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions for class 9 science

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

NCERT Solutions for class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT Solutions for Class 10 Science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

NCERT Solutions for class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT solutions for class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals

Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2

Class 12 Maths Important Questions-Application of Integrals

Class 12 Maths Important questions on Chapter 7 Integral with Solutions for term 2 CBSE Board 2021-22

Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22

Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution

strap

08/03/2020 at 7:04 pm

Mｙ spouse and I abѕolutely love your blog and find most of ｙour post’s to be precisely what I’m looking for.
can you offer guest writeгs to ᴡrite cߋntent avaiⅼable for you?

I wouldn’t mind producing a post or elaborating
on a number of the subjects you write concerning heｒe.

Again, awesome site!

Class 10 maths NCERT solutions of chapter 7- Coordinate Geometry

Class 10 maths NCERT solutions of chapter 7- Coordinate Geometry

EXERCISE 7.1

You can see the video -Class 10 Maths NCERT solution of Question no-5 Exercise 7.1 Chapter 7 Coordinate Geometry

You can see the Video also

Class 10 maths NCERT solutions of chapter 7- Coordinate Geometry

EXERCISE 7.2

You can see the video -Class 10 Maths NCERT solution of Question no-1 Exercise 7.2 Chapter 7 Coordinate Geometry

Class 10 maths NCERT solutions of chapter 7- Coordinate Geometry

EXERCISE 7.3

Class 10 maths NCERT solutions of chapter 7- Coordinate Geometry

Exercise 7.4

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions for class 9 maths

NCERT Solutions for class 9 science

NCERT Solutions for class 10 maths

NCERT Solutions for Class 10 Science

NCERT Solutions for class 11 maths

NCERT solutions for class 12 maths

1 thought on “Class 10 maths NCERT solutions of chapter 7- Coordinate Geometry”

About Us

Quick Links

Contact Us

Class 10 maths NCERT solutions of chapter 7- Coordinate Geometry

Class 10 maths NCERT solutions of chapter 7- Coordinate Geometry

EXERCISE 7.1

You can see the video -Class 10 Maths NCERT solution of Question no-5 Exercise 7.1 Chapter 7 Coordinate Geometry

You can see the Video also

Class 10 maths NCERT solutions of chapter 7- Coordinate Geometry

EXERCISE 7.2

You can see the video -Class 10 Maths NCERT solution of Question no-1 Exercise 7.2 Chapter 7 Coordinate Geometry

Class 10 maths NCERT solutions of chapter 7- Coordinate Geometry

EXERCISE 7.3

Class 10 maths NCERT solutions of chapter 7- Coordinate Geometry

Exercise 7.4

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions for class 9 maths

NCERT Solutions for class 9 science

NCERT Solutions for class 10 maths

NCERT Solutions for Class 10 Science

NCERT Solutions for class 11 maths

NCERT solutions for class 12 maths

Related Topics

1 thought on “Class 10 maths NCERT solutions of chapter 7- Coordinate Geometry”

About Us

Quick Links

Contact Us