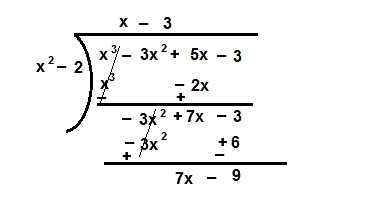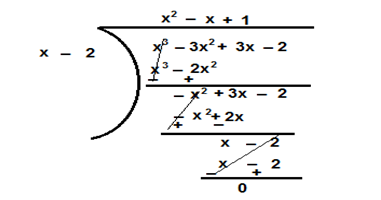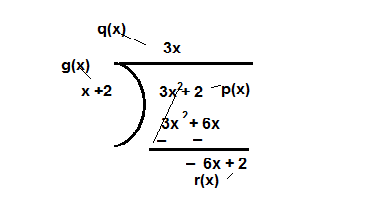Class 10 maths NCERT solution of the chapter 2 polynomial
10 class maths NCERT solutions of the chapter 2 Polynomial are the solutions of unsolved questions of Chapter 2 Polynomial of the NCERT maths textbook of class 10 CBSE . Chapter 2 Polynomial contains the questions based on the polynomial. In the previous class, you would have studied the factors of the polynomial. If you would have understood the topics factorization of the polynomial of the previous class then it will be very easy for you to understand the problems in the 10 class maths NCERT chapter 2 polynomial. If you are needed to clear your concept on polynomial then please go through the post-operation on polynomial.
The NCERT solutions of chapter 2 polynomial are solved by the expert teacher of maths. All questions of chapter 2 polynomial are solved as per the CBSE norms. Each answer of the unsolved questions of chapter 2 polynomial are explained in such a way that every student can understand it. The purpose of the NCERT solutions of chapter 2 polynomial is to help you in your preparation of the unit test, half-yearly, preboard, and CBSE final exam of class 10 board.
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
At the end of this post please don’t forget to write a comment and if you want to update information regarding our future posts then you can subscribe to our website at free of cost. You can study in Future Study Point, NCERT solutions of maths and science, maths and science sample papers, maths and science assignments, guess papers, competitive examinations guide, the e-book of science and maths and the posts on online jobs and your carrier.
NCERT Solutions Class 10 Science from chapter 1 to 16
Follow us on Pinterest
Click here to follow us on Pinterest
NCERT Solutions of class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
See the video -10 class maths NCERT solutions of the chapter 2 :Polynomial
10 class maths NCERT solutions of chapter 2 :Polynomial
Exercise 2.1
Q1. The graphs of y = p(x) are given in the following figure for some polynomial p(x). Find the number of zeroes of p(x) in each case.
Ans.(i) The number of zeroes is 0 because the graph of the polynomial p(x) does not intersect the x-axis.
(ii) The number of zeroes is 1 because the graph of the polynomial p(x) intersects at the x-axis at one point.
(iii) The number of zeroes are 3 because the graph of p(x) intersects the x-axis at 3 points.
(iv) The number of zeroes are 2 because the graph of p(x) intersects the x-axis at two points.
(v) The number of zeroes are 4 because the graph of p(x) intersects the x-axis at four points.
(vi) The number of zeroes are 24because the graph of p(x) intersects the x-axis at 4 points.
See the video for Class 10 exercise 2.1 NCERT Maths Solutions Chapter 2 Polynomial
Exercise 2.2
Q1. Find the zeroes of the following quadratic polynomials and verify the relationship between zeroes and the coefficient.
(i) x² – 2x – 8 (ii) 4s² – 4s + 1 (iii) 6x² – 3 – 7x (iv) 4u² + 8u
(v) t² – 15 (vi) 3x² – x – 4
Solutions.
(i) Factorizing the given polynomial
x² – 2x – 8
x² – 4x + 2x – 8
x( x – 4) + 2( x – 4)
( x – 4)(x +2)
Calculating the zeroes as following
x – 4 = 0, x +2 = 0
x = 4 and x = – 2
a = 1, b= – 2. c = – 8
The relationship between coefficient and zeroes is
2 = 2, – 8 = – 8
In both relationship LHS = RHS, Varified
(ii) The given polynomial is
4s² – 4s + 1
Factorizing it
4s² – 2s – 2s + 1
2s(2s – 1) – 1( 2s – 1)
(2s – 1)(2s – 1)
Calculating the zeroes as following
2s – 1 = 0, 2s – 1 = 0
a = 4, b = – 4, c = 1
The relationship between the coefficient and the zeroes are following
In both cases RHS = LHS, Varified
(iii) The given polynomial is as follows
6x² – 3 – 7x
Arranging it in the standard form ax² + bx + c
6x² – 7x – 3
Factorizing it
6x² – 9x + 2x – 3
3x ( 2x – 3) + 1(2x – 3)
( 2x – 3)(3x +1)
a = 6, b= – 7, c = – 3
The relationship between the coefficient and zeroes of the polynomial is as follows
In both relationship, RHS = LHS, Varified
(iv) We are given the polynomial
4u² + 8u
Factorizing it
4u( u + 2)
Determining its zeroes as following
4u = 0, u +2 = 0
u = 0, u = – 2
a = 4, b= 8, c =0
The relationship between coefficient and zeroes is as follows
In both cases LHS = RHS, Varified
(iv) The given polynomial is
t² – 15
Factorizing the polynomial
t² – (√15)²
(t + √15 )( t – √15)
t + √15 = 0, t – √15 = 0
t = – √15, t = √15
a = 1, b= 0, c = – 15
The relationship between coefficient and zeroes is as follows
0 = 0, –15 = – 15
in both cases ,RHS = LHS, verified
(vi) The given polynomial is as follows
3x² – x – 4
Factorizing the polynomial
3x² –4x + 3x – 4
x ( 3x –4 ) + 1(3x – 4)
( 3x –4 )(x + 1)
Determining the factor as follows
3x –4 = 0, x + 1 = 0
a = 3, b= – 1, c = – 4
The relationship between coefficient and zeroes is as follows
In both cases, it is verified RHS = LHS
See the video for Class 10 exercise 2.2 NCERT Maths Solutions Chapter 2 Polynomial
Q2. Find a quadratic polynomial each with the given numbers as the sum and product of zeroes respectively.
Ans. The sum of zeroes and their product is given to us
If zeroes are α and β, then the quadratic polynomial can be represented as follows
So, we have
Eliminating the denominator by multiplying with 4
4x² – x – 4
So, the required polynomial is 4x² – x – 4
(ii) The sum and product of the zeroes are given to us, so.
If zeroes are α and β, then the quadratic polynomial can be represented as follows
So, we have
Eliminating the denominator by multiplying with 3
3x² –√2x + 1
(iii) We are given the sum and product of zeroes of the polynomial as follows
α + β = 0, αβ = 1
³ – (α + β)x + αβ
x² – 0×x + 1
x² + 1
So, the required polynomial is x² + 1
(iv) The sum of the polynomial is = 1 and the product of zeroes is = 1
α + β = 1, αβ = 1
x² – (α + β)x + αβ
x² – x + 1
Therefore the required polynomial is x² – x + 1
(vi) We are given
4x² + x +1
So, the required polynomial is 4x² + x +1
(vi) We are given, The sum of the zeroes is = 4 and the product of zeroes is = 1
α + β = 4, αβ = 1
x² – (α + β)x + αβ
x² – 4x + 1
Therefore the required polynomial is x² – 4x + 1
10 class maths NCERT solutions of chapter 2 :Polynomial
Exercise 2.3
Q1.Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:
(i) p(x)=x³ – 3x² + 5x – 3 , g(x)= x² – 2
(ii)p(x)= x4 – 3x2 + 4x + 5, g(x) = x2 + 1 – x
(iii)p(x)=x4– 5x + 6, g(x) = 2 – x2
Ans. (i) We are given p(x)=x³ – 3x² + 5x – 3 and g(x) = x² – 2
Dividing p(x) by g(x)
Quotient = x – 3 and remainder = 7x – 9
(ii) Dividing x4 – 3x2 + 4x + 5 by x2 + 1 – x
The quotient is x² + x – 3 and the remainder is 8
(iii) We are given p(x)= x4 – 3x2 + 4x + 5, g(x) = x2 + 1 – x
Dividing p(x) by g(x)
The quotient is –x²– 2 and the remainder is – 5x + 10
Q2.Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial.
(i) t2 – 3 , 2t4 + 3t3 − 2t2− 9t −12
(ii) x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2
(iii) x2 + 3x + 1 , x5− 4x3+ x2+ 3x + 1
Ans.(i) Dividing 2t4 + 3t3 − 2t2− 9t −12 by t2 – 3
The second polynomial is divided by the first polynomial
(ii) The first polynomial is x2 + 3x + 1
The second polynomial is 3x4 + 5x3 – 7x2 + 2x + 2
Dividing the second polynomial by the first polynomial
The second polynomial is divided by the first polynomial
(iii) The first polynomial is x2 + 3x + 1
The second polynomial is x5− 4x3+ x2+ 3x + 1
Dividing the second polynomial by the first polynomial
The second polynomial is not divisible by the first polynomial
Q3.Obtain all other zeroes of the polynomial 3x4 + 6x3 – 2x2 – 10x – 5, if two of it’s zeroes are
√(5/3), -√(5/3)
Ans. The given zeroes of the polynomial are
Therefore two of the factors of the polynomial will be
Their product will also be the factor of the given polynomial
Dividing 3x4 + 6x3 – 2x2 – 10x – 5 by
Factorizing the quotient further
3x² + 6x + 3
3x² + 3x + 3x + 3
3x(x + 1) + 3( x + 1)
(x + 1)(3x + 3) = 3(x + 1)(x + 1)
Hence the other two zeroes of the polynomial are –1 and –1
See the video for question 3
Q4.On dividing x3 – 3x2 + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and -2x + 4 respectively. Find g(x).
Ans. The dividend , p(x) =x3 – 3x2 + x + 2, Quotient, q(x) = x – 2 and remainder, r(x) = -2x + 4 , Devisor, g(x) = ?
The relationship between p(x) ,q(x), g(x) and r(x) is given by
p(x) = g(x) .q(x) + r(x)
x3 – 3x2 + x + 2 = g(x) (x – 2) + (-2x + 4)
g(x) (x – 2) = x3 – 3x2 + x + 2 + 2x – 4 = x3 – 3x2 + 3x – 2
Hence the value of g(x) is x² – x + 1
Q5. Give examples of polynomial p(x), q(x), g(x) and r(x) which satisfy the division algorithm and
(i) deg.p(x) = deg.q(x)
(ii) deg.q(x) = deg.r(x)
(iii) deg.r(x) = 0
Ans. (i) deg.p(x) = deg.q(x)
Choosing p(x) = 2x + 2 if it divided by 2 then the q(x) = x +1
So,example of the polynomial p(x), q(x), g(x) and r(x) which satisfy the given condition
p(x) = 2x + 2, q(x) = x +1, g(x) = 2, r(x) = 0
degree of 2x + 2 =degree of x + 1
deg.p(x) = deg.q(x) =1
(ii) deg.q(x) = deg.r(x)
Choosing p(x) = 3x² + 2, if it is divided by x + 2
So,example of the polynomial p(x), q(x), g(x) and r(x) which satisfy the given condition
P(x) = 3x² + 2, g(x) = x + 2, r(x) = –6x +2, q(x) = 3x
deg.q(x) = deg.r(x)
(iii) deg.r(x) = 0
Choosing p(x) and g(x) so that r(x) = constant(number)
If we suppose p(x) = 2x + 4 if we divide it by 2 the r(x) =4 and q(x) = x
So, p(x) = 2x + 4, g(x) = 2, r(x) = 4, q(x) = x
deg.r(x) = 0
See the video of question number 4,5 of exercise 2.3 and question number 4 of exercise 2.4
10 class maths NCERT solutions of chapter 2 :Polynomial
Exercise. 2.4
Q1. Verify that the numbers given alongside the cubic polynomial below are their zeroes. Also, verify the relationship between the zeroes and the coefficient in each case.
Ans.
If zeroes of a cubic polynomial are α, β and γ, then the polynomial is structured as follows
It has been proved that given numbers are the zeroes of the given polynomial
The relationship between the coefficient and zeroes of a cubic polynomial is given as
LHS = RHS, Varified
LHS = RHS, Varified
–1 = –1
LHS = RHS, Varified
If zeroes of a cubic polynomial are α, β and γ, then the polynomial is structured as follows
x³ – (2 + 1 + 1) x² + (2 × 1 + 1 × 1 + 1 ×2)x – 2× 1 ×1
x³ – 4x² + 5x – 2
It is verified that the numbers given are the zeroes of the given polynomial
4 = 4
LHS = RHS, Varified
5 = 5
LHS = RHS, Varified
2 = 2
LHS = RHS, Varified
Q2. Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and product of its zeroes as 2,–7, –14 respectively.
Ans. If zeroes of a cubic polynomial are α, β, and γ, then the polynomial is structured as follows
We are given
α + β + γ = 2, αβ + βγ + γα = –7, αβγ = –14
Substituting all these values in the polynomial
x³ – 2x² –7 x + 14
Therefore the required polynomial is x³ – 2x² –7 x + 14
Q3. If the zeroes of the polynomial x³ – 3x² + x + 1 are a – b, a, a + b, find a and b.
Ans. The sum of zeroes of a cubic polynomial is given by
Where α, β, and γ are zeroes of the polynomial and a is the coefficient of x³, b is the coefficient of x², c is the coefficient of x and c is the constant.
Substituting the given values of zeroes in the above relation
3a = 3
a = 1
Applying another relationship between coefficient and the zeroes
Where a is the coefficient of x³ and d is the constant
Putting the values of a = 1
(1 – b)×1 × (1 + b) = –1
1 – b² = –1
b² = 2
b = ±√2
Therefore the values of a =1 and b = ±√2
Q4. If two zeroes of the polynomial x4 – 6x3 – 26x2 + 138x – 35 are 2 ± √3, find other zeroes.
Ans. The zeroes of the given polynomial, x4 – 6x3 – 26x2 + 138x – 35 are as follows
2 + √3 and 2 – √3, therefore, two of the factors of the given polynomial are (x – 2 – √3) and (x – 2 + √3)
So, the product of both factor will also be the factor of the given polynomial
(x – 2 – √3)(x – 2 + √3) = (x – 2)² – √3² = x² – 4x + 4 – 3 = x² – 4x + 1
Dividing x4 – 6x3 – 26x2 + 138x – 35 by x² – 4x + 1
The quotient is x² – 2x – 35, factorizing it further
x² – 2x – 35
x² – 7x + 5x – 35
x ( x – 7) + 5( x – 7)
(x – 7)( x + 5)
x – 7 = 0 ⇒ x = 7
x + 5 = 0 ⇒ x = –5
Therefore the other zeroes of the polynomial are 7 and –5.
Q5.If the polynomial X4 −6x3+ 16x2− 25x + 10 is divided by another polynomial x² – 2x + k, the remainders comes out to be x + a,, find k and a.
Ans. Dividing X4 −6x3+ 16x2− 25x + 10 by x² – 2x + k
According to question remainder is x + a
Comparing it with the remainder we got
x = (2k – 9) x, a = 10 – k( 8 – k)
2k – 9 = 1
k = 5
Putting the value of k =5 in a = 10 – k( 8 – k) = 10 – 5(8 – 5) = 10 – 15 = – 5
Hence the value of k =5 and value of a = – 5
NCERT solutions of class 10 science
Solutions of class 10 last years Science question papers
CBSE Class 10 – Question paper of science 2020 with solutions
CBSE class 10 -sample paper of science
NCERT Solutions for class 9 maths
NCERT Solutions for class 9 science
NCERT Solutions for class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for Class 10 Science
NCERT Solutions for class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions for class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Class 12 Maths Important Questions-Application of Integrals
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution