Skip to content 
Class 10 Maths Chapter 3 Exercise 3.1 -Pair of Linear Equations in 2 Variables NCERT Solutions
The NCERT Solutions for Class 10 Maths Chapter 3 Exercise 3.1 focus on solving problems related to Pair of Linear Equations in Two Variables. This exercise will help you understand how to solve two linear equations involving two variables.
In Class 10 Chapter 3 Maths Exercise 3.1, you will work with problems where two conditions involving two variables are given. Your task is to form two equations based on these conditions, solve them, and then find two or more values for the variables. By drawing the graphs of these equations, you’ll see where the two graphs intersect. The point where they intersect gives the values of x and y, which is the solution to the pair of linear equations.
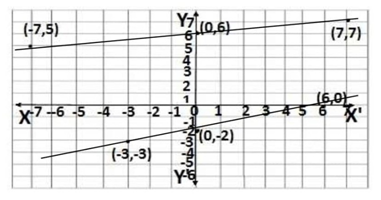
Q1. Aftab tells his daughter,”seven years ago I was seven times as old as you were then. Also three years from now,I shall be three times as old as you will be.”(Isn’t this be interesting?) Represent this situation algebraically and graphically.
Solution. Let the age of Aftab is x and of his daughter is y
According to first condition, seven years ago the age of Aftab = x – 7 and of his daughter =y-7,further it is given that
Seven years back the age of Afteb = 7× Seven years back his daughter’s age
x – 7 = 7(y-7)
x -7 = 7y -49
x – 7y = -49 + 7
x – 7y = -42……(i)
According to second condition,after 3 years the age of Aftab is = x + 3 and of his daughter’s age = y +3,furher it is given that
After 3 years the age of Aftab = 3× His daughter’s age after 3 years
x + 3 = 3(y + 3)
x + 3 = 3y + 9
x – 3y = 6……(ii)
Solutions of the equation x – 7y = -42
| x | 0 | 7 | -7 |
| y | 6 | 7 | 5 |
Solutions of the equation x – 3y = 6
| x | 0 | 6 | -3 |
| y | -2 | 0 | -3 |
Graphical representation of both equations
Q2.The coach of a cricket team buys 3 bats and 6 balls for ₹ 3900. Later, she buys another bat and 3 more balls of the same kind for ₹1300. Represent this situation algebraically and geometrically.
Solution. Let the cost of 1 bat is x and of 1 ball is y
According to fist condition
3 × cost of 1 bat + 6× cost of 1 ball = Rs 3900
3x + 6y = 3900…..(i)
According to second condition
Cost of 1 bat+ 3× cost of 1 ball = Rs 1300
x + 3y = 1300….(ii)
Solutions of equation (i) 3x + 6y = 3900
| x | 100 | -100 | 300 |
| y | 600 | 700 | 500 |
Solutions of equation (ii) x + 3y = 1300
| x | 100 | 400 | -200 |
| y | 400 | 300 | 500 |
Graphical representation of both equations
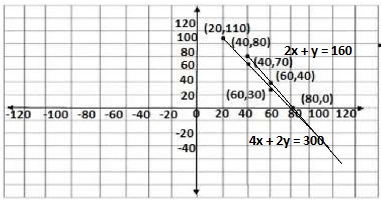
Q3.The cost of 2 kg of apples and 1 kg of grapes on a day was found to be ₹160. After a month, the cost of 4 kg of apples and 2 kg of grapes is ₹300. Represent the situation algebraically and geometrically.
Solution. Let the cost of 1 kg apple is = x and the cost of 1 kg grapes is= y
According to first condition of the question
2×cost of 1 kg apple +cost of 1 kg grapes = Rs 160
2x + y = 160…..(i)
According to second condition of the question
4×cost of 1 kg apple +2×cost of 1 kg grapes = Rs 300
4x + 2y = 300…..(ii)
Solutions of the first equation 2x + y = 160
| x | 80 | 60 | 40 |
| y | 0 | 40 | 80 |
Solutions of the second equation 4x + 2y = 300
| x | 60 | 40 | 20 |
| y | 30 | 70 | 110 |
Graphical representation of both equations
We hope that Class 10 Maths Chapter 3 – Pair of Linear Equations in Two Variables Exercise 3.1 is now clearer to you. If you still have any questions or need further clarification about this exercise, don’t hesitate to ask in the comments. We’re here to help you succeed!
NCERT Solutions of Class 10 Maths
NCERT Solutions of Class 10 Science
