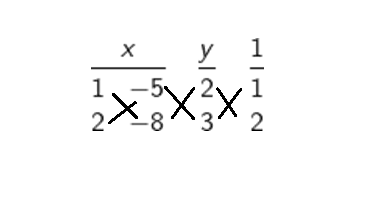NCERT Solutions for Class 10 Maths Exercise 3.5 of Chapter 3 Pair of Linear Equations

NCERT Solutions for Class 10 Maths Exercise 3.5 of Chapter 3 Pair of Linear Equations are helpful for the preparation of the class 10 maths exam and maths worksheet. NCERT Solutions for Class 10 Maths Exercise 3.5 of Chapter 3 Pair of Linear Equations will clear your all doubts whatever you face in doing class 10 maths NCERT chapter 3 Pair of Linear Equations. Chapter 3 of class 10 NCERT Maths is a basic algebraic chapter that is useful in evaluating variables in almost every subject like economics, chemistry, science, physics, business, and accounts. There are three ways of solving a pair of linear equations but here in this exercise, you will study the cross multiplication method of solving a pair of linear equations.

NCERT Solutions for Class 10 Maths  Chapter 3 Linear Equations in Two Variables

Class 10 Maths Sample Paper (Basic) with Solutions for Term 1 CBSE Board Exam 2021-22

Exercise 3.1 -Linear Equations in Two Variables

Exercise 3.2 -Linear Equations in Two Variables

Exercise 3.3-Linear Equation in Two Variables

Exercise 3.4-Pair of Linear Equations

Class 10 maths NCERT solutions of important questions of chapter 3 Pair of Linear Equations

Exercise 3.7 – Linear Equations in Two Variables

NCERT Solutions for Class 10 Maths Exercise 3.5 of Chapter 3 Pair of Linear Equations

Click for online shopping

Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc

Q1.Which of the following pairs of linear equations has unique solutions, no solutions, or infinitely many solutions? In case there is a unique solution, find it by using the cross multiplication method.

(i) x-3y-3=0 and 3x-9y-2=0  (ii) 2x +y =5 and 3x +2y =8

(iii) 3x -5y = 20 and 6x -10y =40 (iv) x -3y -7 =0 and 3x -3y -15 =0

Ans.(i) Given pair of linear equations are x-3y-3=0 and 3x-9y-2=0

Evaluating the ratios of the coefficients and the constants of the equations as follows.

a₁/a₂= 1/3

b₁/b₂=-3/-9 =1/3

c₁/c₂=-3/-2 =3/2

We observe

a₁/a₂ =b₁/b₂ ≠ c₁/c₂

Therefore the given pair of the linear equations has no solution

(ii) The given pair of linear equations is 2x +y =5 and 3x +2y =8

Rearranging the equations into the standard form

2x + y -5=0 and 3x +2y -8 =0

Evaluating the ratios of the coefficients and the constants of the equations as follows.

a₁/a₂= 2/3

b₁/b₂ =1/2

c₁/c₂=-5/-8 =5/8

a₁/a₂≠b₁/b₂

The given pair of the linear equations has a unique solution

Arranging the coefficients and constants of both equations in a matrix as follows

 

 

 

 

x = 2, y = 1

(iii) The given equations are 3x -5y = 20 and 6x -10y =40

Arranging these equations into the standard form

3x -5y – 20=0 and 6x -10y -40 =0

Arranging the coefficients and constants of both equations in a matrix as follows

Evaluating the ratios of the coefficients and the constants of the equations as follows.

a₁/a₂= 3/6=1/2

b₁/b₂ =-5/-10 = 1/2

c₁/c₂=-20/-40 =1/2

It is observed that

a₁/a₂=b₁/b₂= c₁/c₂

Therefore the pair of the equations have infinite solutions

(iv) The given equations are  x -3y -7 =0 and 3x -3y -15 =0

Evaluating the ratios of the coefficients and the constants of the equations as follows.

a₁/a₂= 1/3

b₁/b₂ =-3/-3 = 1

c₁/c₂=-7/-15

It is observed that

a₁/a₂≠b₁/b₂

Therefore the pair of the equations have unique solution

Arranging the coefficients and constants into a matrix as follows

x = 24/6 = 4 and y =-6/6 = -1

Hence the value of x is 4 and the value of y is -1

NCERT Solutions for Class 10 Maths Exercise 3.5 of Chapter 3 Pair of Linear Equations

Q2. (i) For which value of a and b does the following pair of linear equations have an infinite number of solutions?

2x +3y =7

(a -b)x + (a +b)y = 3a +b -2

(ii) For which value of k will the following pair of linear equations have no solution?
3x + y = 1
(2k – 1)x + (k – 1)y = (2k + 1)

We know two linear equations a₁x +b₁y+ c₁=0 and a₂x +b₂y+ c₂=0 have infinite solutions if the ratios between coefficients and constants are as follows.

Arranging the given equations into the standard form

2x +3y -7=0

(a -b)x + (a +b)y -3a -b +2=0

Where a₁=2, b₁=3, c₁=-7 and a₂=a -b, b₂=a +b, c₂=-2a -b +2

We get two equations

2a +2b = 3a -3b

-a +5b =0…..(i)

-9a -3b +6 = -7a -7b

-2a +4b +6 =0…..(ii)

Multiplying equation (i) by 2,we get equation (iii)

-2a + 10b =0…..(iii)

Subtracting the equation (iii) from the equation (ii)

-6b + 6=0

-6b = -6

b =1

Putting the value of b in equation (i)

-a +5×1 =0

-a +5 = 0

-a = -5

a = 5

Hence the required values of a,b are 5 and 1 respectively

(ii) The given pair of the equations is

3x + y = 1
(2k – 1)x + (k – 1)y = (2k + 1)

We know two linear equations a₁x +b₁y+ c₁=0 and a₂x +b₂y+ c₂=0 have no solutions if the ratios between coefficients and constants are as follows.

Arranging the given equations into the standard form

3x + y – 1=0
(2k – 1)x + (k – 1)y -(2k + 1)=0

Where a₁=3, b₁=1, c₁=-1 and a₂=2k-1, b₂=k-1, c₂=2k+1

3k -3 = 2k -1

k = -1 +3 =2

Therefore for k=2 , the given pair of linear equations have no solution

Amazon online Cloths

NCERT Solutions for Class 10 Maths Exercise 3.5 of Chapter 3 Pair of Linear Equations

Q3.Solve the following pair of linear equations by the substitution and cross-multiplication methods:
8x + 5y = 9, 3x + 2y = 4

Ans. The given pair of linear equations is

8x + 5y = 9….(i)

3x + 2y = 4….(ii)

Taking equation (i) and solving it for the value of x

8x = 9-5y

x = (9 -5y)/8

Putting the value of x in equation (ii)

3×(9-5y)/8 + 2y =4

27/8 -15y/8 +2y = 4

27/8 – (15y -16y)/8 = 4

(27 -15y +16y)/8 = 4

(27 +y)/8 =4

27 +y = 32

y = 5

Putting the value of y in equation (i)

8x + 5×5 = 9

8x +25 =9

8x = -16

x = -2

Hence the value of x is -2 and the value of y is 5

(ii) Arranging the given pair of linear equations into standard form

8x + 5y – 9=0…..(i)

3x + 2y -4=0….(ii)

Arranging the coefficients and constants into a matrix as follows

x =-2 and y =5

Hence the value of x is -2 and the value of y is 5

NCERT Solutions for Class 10 Maths Exercise 3.5 of Chapter 3 Pair of Linear Equations

Q4. Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method:

(i) A part of monthly hostel charges is fixed and the remaining depends on the number of days one has taken food in the mess. When a student A takes food for 20 days she has to pay Rs.1000 as hostel charges whereas a student B, who takes food for 26 days, pays Rs.1180 as hostel charges. Find the fixed charges and the cost of food per day.

Ans.Let the monthly fixed charges of the hostel is x and the cost of food per day is y

According to first condition

x + 20y = 1000…(i)

According to second condition

x + 26y = 1180…(ii)

Substracting equation (ii) from equation (i)

-6y = -180

y = 30

Putting the value of y in equayion (i)

x + 20×30 = 1000

x + 600 = 1000

x = 1000 -600 =400

Hence fixed charges is Rs 400 and cost of food per day is Rs 30

(ii) A fraction becomes 1/3 when 1 is subtracted from the numerator and it becomes 1/4 when 8 is added to its denominator. Find the fraction.

Ans.Let the denominator of the fraction is x and the numerator is y

According to the first condition of the question

(y-1)/x = 1/3

3y-3 = x

3y -x = 3….(i)

According to the second condition of the question

y/(x +8) =1/4

4y = x +8

4y -x =8…..(ii)

Substracting equation (ii) from equation (i)

-y =-5

y =5

Putting the value of y in equation (ii)

4×5 -x = 8

x = 20 -8 =12

(iii) Yash scored 40 marks in a test, getting 3 marks for each right answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks been deducted for each incorrect answer, then Yash would have scored 50 marks. How many questions were there in the test?

Ans.Let the correct answers Yash solved in the exam = x and wrong answers are =y

According to first condition of the question

Total marks of Yash in a test =Marks in one correct answer × Number of correct answers + Marks in wrong answer × Number of wrong answers

40 = 3x + (-1)y = 3x -y

3x -y = 40……(i)

According to second condition

4x -2y = 50…..(ii)

Multiplying equation (i) by 2,we get equation (iii)

6x – 2y = 80….(iii)

Substracting equation (iii) from equation (ii)

-2x  = -30

x = 15

Putting the value of x in equation (i)

3×15 -y = 40

45 -y = 40

y =  45-40 = 5

Hence total questions in the test are = Number of correct answers + Number of wrong answers = x + y = 15 +5 = 20

(iv) Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars?

Ans. Let the speed of the car which starts from the place A is = x km/h and the speed of the car which starts from the place B is =y km/h

According to first condition

The car from A travels the distance in 5 h = Speed ×Time = x×5 = 5x km

The car from B travels the distance in 5 h = Speed ×Time = y×5 = 5y km

As per the fig.

5x -5y = 100…..(i)

According to second condition,if both of the cars travels in opposite direction

The car from A travels the distance in 1 h = Speed ×Time = x×1 = x km

The car from B travels the distance in 1 h = Speed ×Time = y×1 = y km

As per the fig.

x +y =100…..(ii)

Multiplying the equation (ii) by 5,we get equation (iii)

5x + 5y = 500…..(iii)

10 x = 600

x = 60

Putting the value of x in equation (ii)

60 + y = 100

y =100 -60 =40

Hence the speeds of the cars which start from the place A is 60 km/h and from place B is 40 km/h

(v) The area of a rectangle gets reduced by 9 square units, if its length is reduced by 5 units and breadth is increased by 3 units. If we increase the length by 3 units and the breadth by 2 units, the area increases by 67 square units. Find the dimensions of the rectangle.

Ans.Let the length of the rectangle is x and the breadth of the rectangle is y

∴ Area of the rectangle is =Length ×Breadth = xy

According to first condition of the question

(x -5)(y+3) = xy -9

xy + 3x -5y -15 = xy -9

3x -5y = 6…..(i)

According to second condition of the question

(x +3)(y+2) = xy +67

xy + 2x +3y +6 = xy +67

2x +3y = 61…..(ii)

Multiplying equation (i) by 2 and equation (ii) by 3,we get equation (iii) and equation (iv)

6x -10y = 12…..(iii) and 6x + 9y =183….(iv)

Substracting equation (iv) from the equation (iii)

-19y = -171

y =171/19 = 9

Putting the value of y in equation (i)

3x -5×9 =6

3x -45 =6

3x = 6 + 45 = 51

x = 51/3 = 17

Hence the length of the rectangle is 17 units and the breadth is 9 units

You can compensate us by donating any amount of money for our survival

Our Paytm No 9891436286

NCERT Solutions of  Science and Maths for Class 9,10,11 and 12

NCERT Solutions of class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions of class 9 science 

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

CBSE Class 9-Question paper of science 2020 with solutions

CBSE Class 9-Sample paper of science

CBSE Class 9-Unsolved question paper of science 2019

NCERT Solutions of class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT solutions of class 10 science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

Solutions of class 10 last years Science question papers

CBSE Class 10 – Question paper of science 2020 with solutions

CBSE class 10 -Latest sample paper of science

NCERT solutions of class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT solutions of class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals