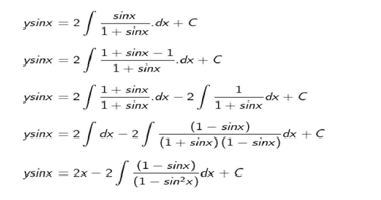Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Importance of Class 12 Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2 with Solutions
Class 12 Maths Sample Paper for Term 2 CBSE Board Exam with Solution is created hereby Future Study Point for helping class 12 maths students in their preparation of the term 2 exams CBSE Board. Students are required to practice this sample paper with proper understanding because this is the solution of the question paper published by the CBSE Board for 2021- 22.By studying Class 12 Maths Sample Paper for Term 2 CBSE Board Exam with Solution, the students can plan the study of maths for better preparations. All the questions of the Class 12 Maths Sample Paper for Term 2 CBSE Board Exam with Solution are solved by a maths expert of CBSE by a step-by-step method.
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE
Class 12 Maths Important Questions-Application of Integrals
The points on Class 12 Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
1. This question paper contains three sections – A, B and C. Each part is compulsory.
2. Section – A has 6 short answer type (SA1) questions of 2 marks each.
3. Section – B has 4 short answer type (SA2) questions of 3 marks each.
4. Section – C has 4 long answer-type questions (LA) of 4 marks each.
5. There is an internal choice in some of the questions.
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
6.Q14 is a case-based problem having 2 subparts of 2 marks each
Marking Scheme Time duration 2 hour
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Section A
Q1.Find
Ans. The given function is
Adding and subtracting 1 in the numerator
……(i)
Putting it in equation (i)
OR
Find
t =cos2x
dt/dx = 2cosx.(-sin x) =-2sinx.cosx =-sin 2x
dt = -sin 2x.dx
-dt = sin 2x.dx
Substituting sin 2x.dx by -dt and t =cos2x
Substituting t =cos2x
Q2.Write the sum of the order and the degree of the following differential equation:
Ans. The given differential equation is
y” = 5
Order of derivative is 2
Degree of y” is 1
Hence the sum of the order and the degree = 2 +1 =3
Q3.If 𝑎̂ and 𝑏̂ are unit vectors, then prove that
Where θ is the angle between them.
Ans. It is given that 𝑎̂ and 𝑏̂ are unit vectors
Q4.Find the direction cosines of the following line:
Ans. The given line is
The direction ratios are 1,1 and 4
The direction cosines will be
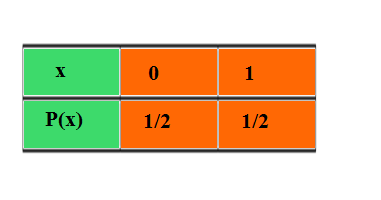
Q5.A bag contains 1 red and 3 white balls. Find the probability distribution of the number of red balls if 2 balls are drawn at random from the bag one-by-one without replacement
Ans. Total balls are given (1+3=4)
Let the number of red balls drawn be x
The cases if 2 balls are drawn at random from the bag one-by-one without replacement
First case: The number of red balls drawn is 0 i.e x =0
P(x =0) = Probability that the first ball drawn is white× Probability that the second ball drawn is white
P(x =0) =( 3/4)×(2/3)=1/2
Second case: The number of red balls drawn is 1 i.e x =1
P(x =1) = Probability that the first ball drawn is red× Probability that the second ball drawn is white+Probability that the first ball drawn is white× Probability that the second ball drawn is red
P(x =1) =( 1/4)×(3/3)+( 3/4)×(1/3)
P(x=1) = 1/4+ 1/4 = 1/2
Therefore probability distribution of the number of red balls is
Q6.Two cards are drawn at random from a pack of 52 cards one by one without replacement. What is the probability of getting the first card red and the second card, Jack?
Ans. Probability of getting the first card red and the second card, Jack
= Probability that the first card drawn is red but not jack×Probability that second card drawn is jack if first is not red +Probability that the first card drawn is red jack×Probability that the second card drawn is red if first is red jack
=(24/52)×(4/51) + (2/52)×(3/51)
= (96/(52×51) + (6/(52×51)
=(96+6)/(52×51) =
=102/(52×51) =2/52 =1/26
Section B
Q7. Find
Ans. Let
x + 1 = Ax² +Bx +C + Cx²
x + 1 = x²(A +C)+Bx +C…..(i)
A,B and C are constants
Putting x =0,in equation (i)
C =1
Putting x =1 and C =1 in equation (i)
A +1-B+1 =2
A+B = 0
A = -B……..(ii)
Putting x =-1 and C =1,A=-B in equation (i)
-1 + 1 = (-1)²(A +1)-A(-1) +1
A +1 +A +1 =0
2A +2 =0
A = -2/2 =-1
B =1
Substituting the values A =-1,B =1 and C =1
Integrating it both sides
Let t = x² +1
dt/dx =2x
dt = 2x.dx
x.dx = dt/2
Therefore
Q8.Find the general solution of the following differential equation:
Ans. The given equation is
Which is a homogeneous differential equation
Let v =y/x
y = vx
Differentiating both sides
dy/dx = x dv/dx +v
Subtituting the value v=y/x and dy/dx
x dv/dx +v =v -sin v
x dv/dx = -sinv
dv/sinv = -dx/x
cosec v.dv = -dx/x
Integrating both sides
∫ cosec v.dv = -∫dx/x
Taking antilog both sides
Therefore the required solution is
OR
Find the particular solution of the following differential equation, given that y = 0 when x = 𝜋/ 4 :
dy/dx +y cotx = 2/(1 +sin x)
Ans. The given differential equation is
dy/dx +y cotx = 2/(1 +sin x)
Comparing the standard form of the linear differential equation
dy/dx +Py = Q
Where P = cot x,Q = 2/(1 +sin x)
Evaluating its Integrating Factor(IF)
IF = e∫Pdx
IF = e∫cotx dx
∫cotx = log(sinx)
IF = elog(sinx)
IF = sinx( as elogx = x)
Solution is given by
y ×IF = ∫(Q×IF) dx +C
Where C is a constant
y sinx =∫(Q×sinx) dx +C
ysinx =2x -2tanx +2secx +C
It is given that y = 0 when x = 𝜋/ 4
0×sinx =2x -2tan(𝜋/4) +2sec(π/4) +C
2π/4- 2 ×1+ 2×√2 +C =0
C = 2 -2√2 – π/2=2(1 -√2) – π/2
Hence
ysinx =2x -2tanx +2secx +2(1 -√2) – π/2
Q9. If
Then show that
Ans. It is given that
are perpendicular to each other
It is also given that
are parallel to each other
can’t be both parallel and perpendicular
Therefore
Q10.Find the shortest distance between the following lines:
Ans. The given lines are
Rewritting the given lines
Since parallel vectors are same i.e
The vectors equations of two parallel lines are given as
The distance(d) between these parallel vector is given as
Comparing the given vectors
Now,we have
= i(3×1-1×0) -j(2×3-1×0) +k(2×0-1×0)
Therefore the shortest distance between the given lines is
Q11.Evaluate
Ans. Factorizing
x³ -3x² +2x
x[x² -3x +2]
x[x² – x-2x +2]
x[x(x -1) -2(x -1)]
x(x-1)(x -2)
∴ The critical point of the function are
x =0, x =1,x =2
Now,we have
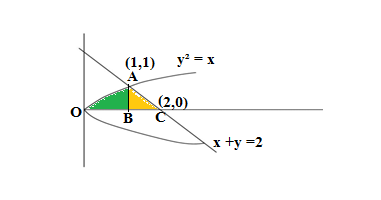
Q12.Using integration, find the area of the region in the first quadrant enclosed by the line x + y = 2, the parabola y 2 = x and the x-axis.
Ans. Drawing the graph of line x + y = 2, the parabola y² = x and the x-axis.
Solving x + y = 2 and y² = x
Putt y = 2-x in the equation y² = x
(2 -x)² = x
4 +x² – 4x -x =0
x² -5x +4 =0
x² -4x -x+4 =0
x(x -4) -1(x -4) =0
(x -4)(x -1) =0
x = 4,1
Since x=1 < 2, so y =1,therefore the point of intersection of x +y =2 and y²=x is (1,1)
The area enclosed by the curve, given line, and x-axis is AOB
Area of AOC = Area of AOB + Area of BAC
y =±√x , considering y =√x ,since we have to find the area in the first quadrant
And from the equation of the line ,we have y = 2 -x
Area of AOC =Integration of √x within the limits 0 and 1 + Integration of 2-x within the limits 1 and 2
Area of AOC = (1/3/2) +2(2-1) -[2²/2 -1²/2]
Area of AOC = 2/3 +2 -(2 -1/2)
Area of AOC = 2/3 +2 -3/2 =(4+12-9/6)= 7/6
Hence area of AOC is 7/6 square unit
You can compensate us by donating any amount of money for our survival
Our Paytm No 9891436286
CBSE Class 9-Question paper of science 2020 with solutions
CBSE Class 9-Sample paper of science
CBSE Class 9-Unsolved question paper of science 2019
NCERT Solutions for class 9 maths
NCERT Solutions of class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
CBSE Class 10 – Question paper of science 2020 with solutions
CBSE class 10 -Latest sample paper of science
Solutions of class 11 maths question papers
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions of class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |