Solutions of Class 11 maths test unit

Recently an online school test of 11 class CBSE students was held in November 2020.Here the school test of G.D Lancer Public School is taken by the maths faculty of the school in which a  question paper containing 20 MCQ   questions were asked to complete it in 40 minutes.Here we have solved the given question paper so that all online students could be benifitted by studying the way of solving the questions available in the question paper.

Hence you can study NCERT Solutions of maths and science from class 9 to 12, carrier oriented article, sample papers and solutions of previous year question papers, trips for developing your maths skill and our blogs about different plateforms for online jobs.

 

Solutions of Class 11 maths test unit-2 G.D Lancer Public School,New Delhi

Click for online shopping

Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc

Q1.Three identical dice are rolled. The probability that the same number will appear on each of them is

Ans. Total number of possible outcomes = 6³ = 216

The favorable outcome = The Same number will appear on each of them

The number of cases(i.e 6)  that the Same number will appear on each of them are =(1,1,1), (2,2,2), (3,3,3)……(6,6,6)

Let the probability of this event (E) is P(E)

Therefore the answer is (b)

Q2.There are four machines and it is known that exactly two of them are faulty. They are tested, one by one, in a random order till both the faulty machines are identified. Then the probability that only two  tests are needed is

Ans. The number of total possible outcomes that machines may be faulty

Let machines are A,B, C and D, the number of outcomes that two machines are faulty

(A,B), (B,C), (C, D), (D,A),(A,C),(B,D)…

Here order is not important so calculating the total number of such combinations when there exist exactly two faulty machines are →

Only two test are taken one by one [i.e means either of the test, ex.(A,B)]for choosing two machines are faulty, so the favorable outcomes are = 1

 

Q3.Two unbiased dice are thrown. The probability that neither a doublet nor a total of 10 will appear is

Ans. The total number of outcomes we get after throwing two dice= 6×6 = 36 ( i.e the outcomes we get by throwing one dice =6)

Let the event of showing a doublet is shown by A and event of showing the sum 10 of outcomes on both dice by B

The  outcomes showing the doublets are =(1,1), (2,2),(3,3),(4,4),(5,5),(6,6)

P(A) = 6/36 = 1/6

The  outcomes showing the sum(10) of outcomes are = (4,6),(5,5),(6,4)

P(B) = 3/36 = 1/12

Then the event of showing a doublet and sum of 10 is A∩B and the event of showing either a doublet or sum of 10 of outcomes on both dice is A∪B

The outcomes showing a doublet and sum of 10 are =(5,5)

So,  P(A∩B) = 1/36

The P(A∪B) is given by

P(A∪B) = P(A) + P(B) – P(A∩B)

= 1/6 + 1/12 – 1/36 = 2/9

Therefore the probability of neither a doublet nor a sum of 10 is given as following

= 1- 2/9 = 7/9

Hence, the answer is  (d)

Q4.A bag contains 5 brown and 4 white socks. A man pulls out two socks. The probability that both the socks are of the same color is

Ans. The total number of ways of choosing two socks out of (5+4 =9) socks

The number of ways of choosing the socks of same colours are = The number of ways of choosing brown socks + The number of ways choosing brown socks.

Q5.There are 12 points in a plane out of 5 are collinear. The number of triangles formed by the points as vertices is

(a)185

(b)210

(c)220

(d)175

Ans.Number of verteces in a triangle are = 3

Out of 12 points the number of ways of choosing 3 points in the formation of triangle are ¹²C₃

= 2 × 11 × 10 = 220

Among 12 points 5 points are collinear,so the number of choosing 3 points out of 5 are =⁵C₃

⁵C₃ are the ways from which we can’t form triangles

Therefore the number of triangles formed by the points are  = 220 – 10 = 210

Hence the answer is (b)

Q6.If repetition of the digits is allowed, then the number of  even natural numbers having three digits is

(a)250

(b)350

(c)450

(d)550

Ans. The three-digit even numbers are formed when once place digit is even

The number of ways of placing the digit in once place =5

Since repetition of the digit is allowed so the number of placing the digit in hundred place = 10

Since 0 in thousand place in forming three-digit even numbers supposed as two-digit numbers, therefore the number of ways of placing the digit in thousand place = 9

Therefore the total number of ways of forming three-digit even numbers

= 5 × 10× 9 = 450

Therefore the answer is (c)

Q7.The number of ways in which 8 distinct toys can be distributed among 5 children is

(a)5⁸

(b)8⁵

(c)⁸P₅

(d)⁵P₅

Ans. Since 8 toys are distinct

So, the number of ways, a toy is distributed = 5

Toys are = 8

Therefore the number of ways of distributing 8 toys

= 5 ×5 ×5 ×5 ×5× 5 ×5 ×5 = 5⁸

Hence the answer is (a)

Please follow us on pintrest

Pintrest future study point

Q8.6 men and 4 women are to be seated in a row so that no two women sit together. The number of ways they can be seated is

(a)604800

(b)17280

(c)120960

(d)518400

Ans. 6 men and 4 women are to be arranged so that no two women sit together in the following ways

M W M W M W M W MM

There are 6 positions where a man can be seated

The number of ways 6 men can be placed in 6 positions in relation to women

6! = 6 × 5×4×3×2×1 = 720

In these 720 ways a man can be placed in 5 positions  in relation to 4 women as following

A man can be placed in  5 positions by = 5 ways

Therefore total number of ways the men are arranged to be seated= 720 × 5 = 3600

The number of ways 4 women can be placed in 4 positions

4 ! = 4 × 3 ×2 = 24

An woman can be placed in  5 positions by = 5 ways

So, total number of ways 4 women can be placed = 5×24 = 120

Hence total number of ways 6 men and 4 women can be seated in the case when two women are not seated together

= 3600 ×120 = 432000 ways.

Q9.The number of ways can the letters of the word ASSASSINATION be arranged so that all the S are together is

(a)152100

(b)1521

(c)15120

(d)151200

Ans. Since we need to assigned 4S together,

We consider 4S as one block SSSS

So, our letters become SSSS A A I N A T I O N

We arrange them now

since letters are repeating

Hence we use this formula

Here,4 letters must be supposed as a single object

n = letters to be arranged = 9 + 1 = 10

Since 3A,2I,2N

P₁ = 3, P₂ = 2, P₃ = 2

Number of arrangements where S’s are together

 

= 151200

Q10.Let T_n denote the number of triangles which can be formed using the vertices of a regular polygon on n sides. If T_n+1 – T_n = 21, then n equals.

(a)5

(b)7

(c)6

(d)4

Ans. Since it is given to us that  T_n is the number of triangles which can be formed using the vertices of a regular polygon on n sides

T_n  =The number of ways of forming the triangles out of n vertices are = ⁿC₃

We are given the condition

T_n+1 – T_n = 21

ⁿ⁺¹C₃ – ⁿC₃ = 21

n(n -1) = 42

n² – n – 42 = 0

n² -7n +6n -42 = 0

n(n – 7) + 6(n – 7) = 0

(n – 7)(n + 6) = 0

n = 7,n = -6

Neglecting n = -6,since the number of vertices or sides of polygon can’t be negative

Therefore n = 7,hence answer is (b)

Q11.How many ways are here to arrange the letters in the word GARDEN with the vowels in alphabetical order?

(a)120

(b)240

(c)360

(d)480

Ans.The total number of ways of arranging the letters in the GARDEN.

= 6!

The number of ways of arranging two vowels(A,E) in alphabetical order= 2!

The required number of ways of arranging the letters = 6!/2! = 360

Q12.A student is to answer 10 out of 13 questions in an examination such that he must choose at least 4 from the first five questions. The number of choices available to him is

(a)40

(b)196

(c)280

(d)346

Ans.The number of ways of choosing at least 4 questions from the first 5 questions = ⁵C₄= 5 ways

Out of the Remaining (13-5=8) questions he has to do questions by=⁸C₆

ways

The number of of ways of choosing first 4 question o/f 5 and remaining 6 questions o/f 8 are =5 × ⁸C₆

If he selects the first 5 questions then he has to choose another 5 questions out of the remaining 8 questions =

Therefore the total number of required ways = 140 × 56 = 196

Hence answer is (b) 196

Q13.How many 3-letter words with or without meaning, Can be formed out of the letters of the word, LOGARITHMS if repetition of letters is not allowed

(a)720

(b)420

(c)none of these

(d)5040

Ans. Since all 10 letters of the given word LOGARITHMS are distinct to each other and repition is not allowed.

So,the number of ways of forming words of 3 letters are = ¹⁰P₃

¹⁰P₃

Hence the answer is (a) 720

Q14.The equation of straight lines passing through the point (1,2) and parallel to the line y = 3x + 1 is

(a)y + 2 = 0

(b)y + 2 = 3(x+1)

(c)y – 2 = 3(x-1)

(d)y -2 = x – 1

Ans. The equation of a straight line passing through (x,y) is given by

Y –y = m(X- x), where m = slope of the line

The given line is y = 3x + 1

Slope (m)of the given is = dy/dx

Since the line is parallel to a given line so the slope of both of them must be equal to each other

Therefore the required equation of the line passing through (1,2) is

y -2 = 3(x -1)

Hence the answer is (c) y – 2 = 3(x-1)

Q15.The equation of the line which cuts off equal and positive intercepts from the axis and passes through the point  (α,β) is

(a)x + y = α + β

(b)x + y = α

(c)x + y = β

(d)None of these

Ans. The equation of the line by intercept form is given by

Where a is X intercept and b is Y-intercept

Since it is given to us a = b and the line is passing through (α,β)

So,the equation can be rewritten as following

a = α + β

Substituting the value of a in the equation

x + y = α + β

Therefore the answer is (a)x + y = α + β

Q16.The angle between the lines x – 2y = 2 and y – 2x = 5 is

(a)tan^-1(1/4)

(b)tan^-1(3/5)

(c)tan^-1(3/4)

(d)tan^-1(2/3)

Ans. The slope m₁ of the line x – 2y = 2 and of the line y – 2x = 5 is given as following.

x – 2y = 2

y – 2x = 5

Let the angle between both of the line is θ,which is given by

Therefore answer is (c) tan^-1(3/4)

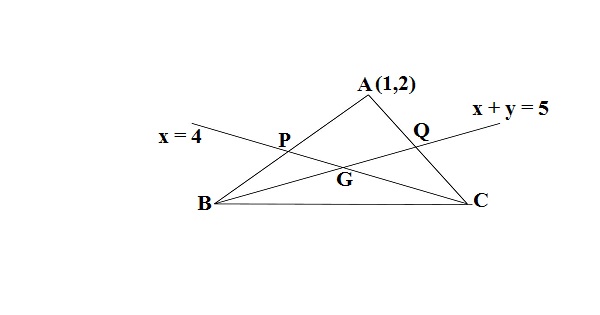
Q17.In a ΔABC the coordinates of A are (1,2) and equations of the median through B and C are respectively x + y = 5 and x  = 4, then coordinates of B are

(a) (1,4)

(b)(7,-2)

(c) None of these

(d) (4,1)

Ans.

Since the lines x +y=5 is passing through  B,so let x =a ,then coordinates of B are (a, 5-a) ,the CP is the median,the coordinates of P are[ (a+1)/2,(5-a +2)/2] it should satisfy the equation  x = 4

(a+1)/2 = 4 ⇒a = 7, coordinates of B are (7, -2)

Hence,answer is b(7, -2)

Q18.The length of the perpendicular from the origin to a line is  7 and the line makes an angle of 150 degrees with the positive direction of the y-axis. then the equation of line is

(a)x + y = 14

(b)√3y + x = 14

(c)√3y + y = 14

(d)None of these

Ans.  The length of the perpendicular from the origin to a line,p=  7

The line makes an angle  with the positive direction of the y-axis=150°

Let AB be the given lines that make an angle of 150° with the positive direction of the y-axis and OA be the perpendicular drawn from the origin on the line.

Here, p = 7 and α = 30°

So, the equation of the line AB is

xcosα + ysinα = p

xcos30° + ysin30° = 7

√3x/2 + y/2 = 7

√3y + y = 14

Q19.The sum of squares of the distances of a moving point from two fixed points (a, O) and (-a,0) is equal to 2c² then the equation of its locus is

(a)x² – y² = c² – a²

(b)x² – y² = c² + a²

(c)x² + y² = c² – a²

(d)x² + y² = c² + a²

Ans. Let P(h, k) be any position of the moving point and let A(a, 0), B(-a, 0) be the given points. then,

PA² + PB² = 2C²

⇒ (h – a)² + (k – 0)² + (h + a)² + (k – 0)² = 2c²

⇒ h² – 2ah + a² + k² + h² + 2ah + a² + k² = 2c²

⇒ 2h² + 2k² + 2a² = 2c²

⇒ h² + k² = c² – a²

Hence, equation of locus (h, k) is x² + y² = c² – a²

Q20.The equation of the locus of a point equidistant from the point A(1,3) and B(-2,1) is

(a)6x – 4y = 5

(b)6x + 4y = 5

(c)6x + 4y = 7

(d)6x – 4y = 7

Ans. Let the point on the locus is (h,k)

P(h,k) is equidistance from A(1,3) and B(-2,1)

P(h,k) = [(1-2)/2,(3+1)/2]=(-1/2, 2)

The equation of locus of the point P(h,k) is perpendicular bisector off the joining A(1,3) and B(-2,1)

Slope of the locus

m× slope of locus = -1

2/3 ×slope of locus = -1

slope of locus =-3/2

Equation of locus

⇒ y-k= m(x-h)

= y -2 = -3/2(x +1/2)

= 2y – 4 = – 3x – 3/2

= 2y + 3x = 4 – 3/2

= 2y + 3x = (8 – 3)/2

4y + 6x = 5

Hence the answer is (b)6x + 4y = 5

 

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions for class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions for class 9 science 

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

NCERT Solutions for class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT Solutions for Class 10 Science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

NCERT Solutions for class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT solutions for class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals

Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2

Class 12 Maths Important Questions-Application of Integrals

Class 12 Maths Important questions on Chapter 7 Integral with Solutions for term 2 CBSE Board 2021-22

Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22

Solutions of class 12  maths question paper 2021 preboard exam CBSE Solution