Class 12 Maths Important Questions-Application of Integrals

Q1.Find the area of the region bounded by the curve y² = x and the lines x = 1, x = 4 and x – axis.

Ans. The given curve  y² = x and the lines x =1,x =4

Also given x -axis (i.e y =0)

Drawng the graph of the curve (i.e parabola) y² = x and the lines x =1,x =4 and y=0

The given curve is

y² = x

y = ±√x

Area of the region covered by the parabola and the lines x =1 ,x=4, and X-axis is symmetrical about the X-axis which is shown by the shaded region

∴ Area of ABCD = 2 area ABFE

Area ABFE = Integration of y with respect to x within the limits x =1 and x =2

= 4/3(2³ -1) = 4/3(8 -1) =28/3

Therefore the area of the shaded region is (28/3) square unit

Click for online shopping

Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc

Q2.Find the area of the region bounded by the curves y²=2px and x²=2py.

Ans. Solving equations y²=2px and x²=2py,we get

Putting the value y = √(2px) in the equation x²=2py

x²=2p√(2px)

Squaring both sides

x⁴ =4p²× 2px

x⁴ -8p³x =0

x(x³ -8p³) =0

x =0

x³ -8p³ =0

x³ = 8p³

x = 2p

When x = 0 then y=0 and when x =2p then y²=2p(2p)⇒ y =2p

Therefore area bounded by both curves is shown as shaded region in the following graph

The area of the shaded region = The integration of y with respect to x within the limits x=0 and x=2p

From the curve y²=2px ⇒y =√2px and from the curve x²=2py⇒y=x²/2p

The function representing the shaded region = [√(2px) – x²/2p]

 

=(8p²/3) – (4p²/3)

=4p²/3

The area covered by both curves is (4p²/3) square unit

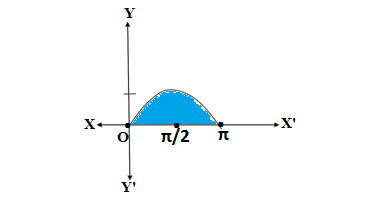
Q3.Find the area of the curve y = sinx, between 0 and π.

Ans. Drawing the curve y = sinx

Area of the curve y = sinx, between 0 and π = Area of the shaded region

Area of the shaded region=Integraion of the function y with respect to x within the limit 0 and π

=-( cos π – cos 0)

= -(-1 -1)

=-(-2) = 2

Hence area of the shaded region is 2 square unit

Q4.Find the area of the region bounded by the two parabolas y = x² and y² = x

Ans. The given curves are y = x² and y² = x

Solving both curves

Putting the value y = x² in the equation y² = x

x⁴=x

x⁴-x=0

x(x³ – 1) =0

x =0, x =1

Putting x =0,y =0 and putting x =1,y=1 indicates that both curves meet at (0,0) and (1,1)

y = x²  and y² = x⇒y = √x

The function representing the shaded region = √x -x² since √x ≥ x²

Area of the shaded region = integration of the function (√x -x²) within the limit 0 and 1

=[2/3 – 1/3] = 1/3

Hence area bounded by the given curves is 1/3 square unit

Q5. Find the area enclosed by the circle x² + y² = 4 and the straight line x + y =2 .

Ans. Solving the equation of the circle and the line

x² + y² = 4⇒ y =√( 4-x²) and y = 2- x

√( 4-x²) = 2- x

Squaring both sides

4 -x² = 4 + x² – 4x

2x² – 4x = 0

x² – 2x = 0

x( x -2) = 0

x =0 and x =2

Putting x = 0 and x =2 in the equation x + y =2

When x = 0,y =2 and when x =2 ,y = 0

The straight line and the circle intersects at (0,2) and (2,0)

Area of the shaded region = Area of the quadrant – Area of the triangle

Area of the quadrant = Integration of the y = √(2² – x²) w.r.t x within the limits x =0 and x =2

= 2×π/2 = π

Area of the quadrant = π square unit

Area of the triangle = (1/2)×2×2 = 2 square unit

Area of the shaded region = (π -2)square unit

Q6.Find the area of the region bounded by the curve y = x³, y = x +6 and y-axis.

Ans. Solving the equation y = x³, y = x +6

Substituting y =x³ in second equation

x³ = x +6

x³ -x -6 =0

x =2 satisfies the above equation

Factorizing the above equation by the remiender theorem

x²(x -2) +2x² -x -6 =0

x²(x -2) +2x(x -2) +4x -x -6 =0

x²(x -2) +2x(x -2) +3x-6 =0

x²(x -2) +2x(x -2) +3(x-2) =0

(x -2)( x² +2x +3) =0

Since the roots of the equation x² +2x +3 are not real,therefore putting x =2 in y = x +6,we get y =8

Hence the curve and the given line intersect at only one point (2,8)

Drawing the graph of y = x³, y = x +6 and y-axis

The shaded region represents the function [(x +6)-x³]

The area of the shaded region =Integrating the function [(x +6)-x³] w r t x within the limits x =0 and x =2

=(2²/2  +6×2 – 2⁴/4]

4/2    +12 –   16/4

=2 +12 -4 = 10 square unit 

You can compensate us by donating any amount of money for our survival

Our Paytm No 9891436286

NCERT Solutions of  Science and Maths for Class 9,10,11 and 12

NCERT Solutions of class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions of class 9 science 

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

CBSE Class 9-Question paper of science 2020 with solutions

CBSE Class 9-Sample paper of science

CBSE Class 9-Unsolved question paper of science 2019

NCERT Solutions of class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT solutions of class 10 science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

Solutions of class 10 last years Science question papers

CBSE Class 10 – Question paper of science 2020 with solutions

CBSE class 10 -Latest sample paper of science

NCERT solutions of class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT solutions of class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals