NCERT Solutions of class 12 maths Miscellaneous exercise -Application of Integrals
The NCERT solutions of miscellaneous exercise of chapter 8-Application of Integrals are a summary of all the methods used in all the exercises of chapter 8-Application of Integrals, therefore in this respect, NCERT solutions of miscellaneous exercise are very important for students.All the questions of miscellaneous exercise are solved by the expert by a step-by-step method so each student will understand the solution clearly.
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
NCERT Solutions of class 12 maths Miscellaneous exercise -Application of Integrals
Exercise 8.1-Application of Integration
Exercise 8.2-Application of Integration
Exercise 8.3-Application of Integration
NCERT Solutions of Maths for Class 12 Miscellaneous exercise -Application of Integrals
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
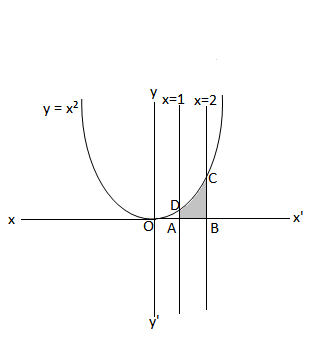
Q1. Find the area under the given curve and given lines
(i) y = x² , x = 1, x =2 and x-axis
(ii) y = x4, x=1, x= 5 and x-axis
Ans.
(i) We are given the curve y = x² and the lines x = 1, x =2
Area covered by the curve,x-axis and the given lines = arABCD
(ii) We are given the curve y = x4, x=1, x= 5 and the lines x = 1, x =2
Area covered by the curve, x-axis and the given lines = arABCD
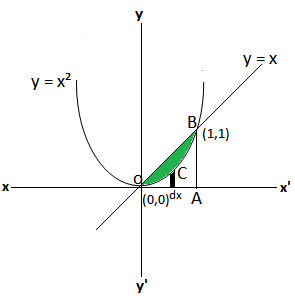
Q2. Find the area between the curves y = x and y = x²
Ans. We are given the equations of curve y = x² and y = x
Putting y = x, in y = x²
x = x² ⇒ x= 0 and x =1,again putting x = 0 and x= 1 in one of the equations, we get y=0 and y=1
Therefore both of curve and the line intersect each other at origin (0,0) and (1,1)
Area covered by the line and the curve , area OCB = ar ΔOAB – ar OABCO
ar OABCO = 1/3 sq.unit
OA = 1 unit and AB = 1 unit
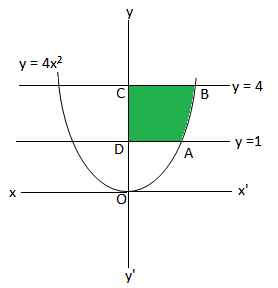
Q3. Find the area of the region lying in the first quadrant and bounded by y = 4x², x = 0, y =1 and y = 4.
Ans. The given curve is y = 4x² and the lines are x = 0, y =1 and y = 4.
The area covered by the curve y = 4x² and the lines are x = 0(y-axis), y =1, and y = 4 is ar ABCD
From the equation of curve, y = 4x², we have
Q4. Sketch the graph of and evaluate
rom the equation of curve, y = 4x², we have
Latest Laptops and Desktops on very small EMI:no extra cost
Q4. Sketch the graph of and evaluate
Ans.Solutions of the given equation
| x | -6 | -5 | -4 | -3 | -2 | -1 | 0 |
| y | 3 | 2 | 1 | 0 | 1 | 2 | 3 |
The graph of the given equation is drawn as follows
= – 9 + 18 = 9
Q5. Find the area bounded by the curve y = sinx between x = 0 and x = 2π.
Ans.The graph of the curve y = sinx between x = 0 and x = 2π, is shown below
The area bounded by the curve y = sinx, x = 0 and x = 2π
=Area of OAB + area of BCD
= 2 + 2 = 4 sq.unit
You can study
Click the link here for rest of the solutions or study the following
Class 11 Chemistry
Chapter 1-Some basic concepts of chemistry
Class 11 Physics
Paytm number 9891436286
The money collected by us will be used for the education of poor students who leaves their study because of a lack of money.
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions for class 9 maths
NCERT Solutions for class 9 science
NCERT Solutions for class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for Class 10 Science
NCERT Solutions for class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions for class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Class 12 Maths Important Questions-Application of Integrals
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution



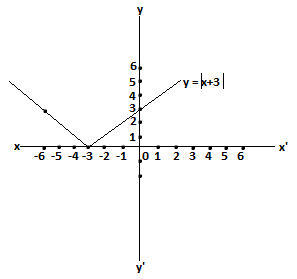




This web site truly has all of the information I wanted concerning this subject and didn’t know who to
ask.