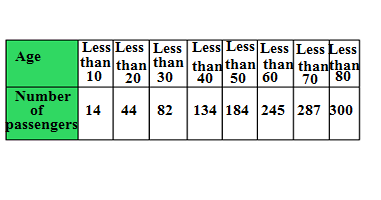Skip to content 
Solution of Class 10 Maths(Basic) Sample Paper Published by CBSE for Term 2, 2022
Solution of Class 10 Maths(Basic) Sample Paper Published by CBSE for Term 2, 2022 is created here for helping class 10 maths students to boost their preparation for CBSE Board term 2 exams.
(i) Class 10 Maths(Basic) Sample Paper consists of 14 questions divided into three section.
(ii) Section A of Class 10 Maths(Basic) Sample Paper comprises of 6 question of 2 marks each,internal choice has been provided in two questions.
(iii)Section B of Class 10 Maths(Basic) Sample Paper comprises of 4 question of 3 marks each,internal choice has been provided in one question
(iv). Section C of Class 10 Maths(Basic) Sample Paper comprises of 4 questions of 3 marks each, internal choice has been provided in two questions.
Solution of Class 10 Maths(Basic) Sample Paper Published by CBSE for Term 2, 2022
Q1.Find the roots of the quadratic equation 3x² − 7x − 6 = 0.
Ans. The given quadratic equation is 3x² − 7x − 6 = 0
Factorizing the given quadratic equation
3x² − 7x − 6 = 0
3x² − 9x +2x− 6 = 0
3x(x -3) +2(x -3) =0
(x -3)(3x +2)= 0
x =3,-2/3
OR
Find the values of k for which the quadratic equation 3x² + kx + 3 = 0 has real and equal roots.
Ans.The given quadratic equation is 3x² + kx + 3 = 0
Since given quadratic equation has real and equal roots
We know a quadratic equation ax² + bx + c = 0 has real and equal roots when
D =b²- 4ac =0,where D is called the discriminant of the quadratic equation
In the given equation we have
a =3, b =k and c =3
k² -4×3×3 =0
k² – 36 =0
k² =36
k =±6
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
Q2.Three cubes each of volume 64cm³ are joined end to end to form a cuboid. Find the total surface area of the cuboid so formed?
Ans. The given volume of each cube = 64cm³
The volume of a cube is = a³
∴ a³ =64
a = 4
The side of each cube is 4 cm
Since 3 such cubes are joined end to end to form a cuboid
Therefore the length(l) of the cuboid is =3×4 =12 cm
Breadth(b) of the cuboid is =4 cm
Height(h) of the cuboid is =4 cm
Total surface area of the cuboid is given by
TSA= 2(lb +bh +hl)
= 2(12×4 +4×4 +4×12)
= 2(48 +16 +48)
=2×112=224
Hence total surface area of the cuboid is 224 cm²
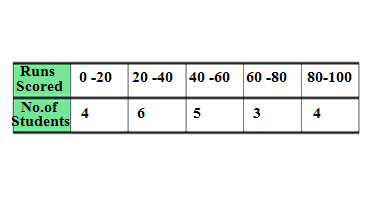
Q3.An inter-house cricket match was organized by a school. The distribution of runs made by the students is given below. Find the median runs scored.
Ans.
| Runs Scored | Number of the students | Cumulative Frequency |
| 0 – 20 | 4 | 4 |
| 20 -40 | 6 | 10(cf) |
| 40(l) – 60 | 5(f) | 15 |
| 60 -80 | 3 | 18 |
| 80 -100 | 4 | 22 |
Median group is =22/2 =11,lies in the class interval 40 -60
Where l =40, n/2 =11, cf =10,f =5 and h =60 -40 =20
= 40 +20/5
= 40 +4 =44
Hence median runs scored by the student is 44
Q4.Find the common difference of the AP 4,9,14,… If the first term changes to 6 and the common difference remains the same then write the new AP.
Ans. The given AP is 4,9,14,…
The common difference(d) of the given AP is
d = 9 – 4 =5
If the first term changes 6 and common difference remains the same i.e 5 then the new AP is
6,11,16,…
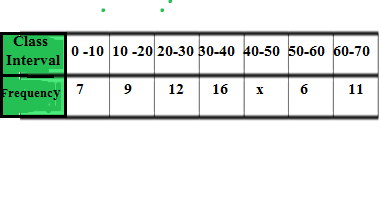
Q5.The mode of the following frequency distribution is 38. Find the value of x.
Ans.
| Class Interval | Frequency |
| 0 – 10 | 7 |
| 10 – 20 | 9 |
| 20 – 30 | 12(f0) |
| 30(l) – 40 | 16(f1) |
| 40 – 50 | x(f2) |
| 50 -60 | 6 |
| 60 – 70 | 11 |
The mode(M) of a data is given as
The given mode ,M(38) of the data lies in the class interval
(40/(32-12-x) = 38 -30
40/(20 -x) =8
160 – 8x = 40
8x = 160 -40
8x = 120
x = 120/8 =15
OR
The given figure, a circle is inscribed in the quadrilateral ABCD. Given AB=6cm,BC=7cm and CD=4cm. Find AD.
Ans.
Let DS = x
DS =DP =x….(i)
Given that AB=6cm,BC=7cm and CD=4cm
Since CD = 4 cm
CS = CD -x = (4-x) cm
CS =CR = (4-x) cm(tangents drawn from an external point of the circle)
BR = BC -CR = [7-(4-x)] cm=[7 -4 +x] =(3 +x)cm
BR = BQ =(3 +x)cm
AQ = AB – BQ =[6-(3+x)] cm=[6 -3 -x] =(3-x)cm
AQ = AP =(3-x)cm…..(ii)
From equation (i) and equation (ii)
DP +AP = x +3 -x =3
AD = 3 cm
Q7.An AP 5, 8, 11…has 40 terms. Find the last term. Also find the sum of the last 10 terms.
Ans.The given AP is AP 5, 8, 11…up to 40 terms
The last term is a40=?,and common difference,d =8 -5 =3
nth term of the AP is given by
an= a +(n -1)d
Where a =5,d =8-5 =3, n=40
a40= 5+(40 -1)3
= 5 +39×3 =5 +117=122
Sum of the last 10 terms
= S40 – S30
=40/2[2×5 +(40-1)×3 ] – 30/2[2×5 +(30-1)×3 ]
=20(10 +39 ×3 )- 15(10 +29×3)
=20(10 +117) -15(10 +87)
=20×127 -15×97
=2540 -1455
=1085
Q8.A tree is broken due to the storm in such a way that the top of the tree touches the ground and makes an angle of 30° with the ground. The length of the broken upper part of the tree is 8 meters. Find the height of the tree before it was broken.
Ans.
Let the tree is AB
The length of the tree,AB = BC + AC
tan 30° = BC/BD =BC/8
1/√3 =BC/8
BC = 8/√3 m
sin 30° = BC/CD =(8/√3)×1/CD
1/2 =8/√3CD
CD = 16/√3
Height of the tree before it was broken
CD +BC=16/√3 +8/√3 =24/√3 =24√3/(√3×√3) =24√3/3 =8√3
Hence Height of the tree before it was broken was 8√3 m
OR
Two poles of equal height are standing opposite each other on either side of the road 80m wide. From a point between them on the road, the angles of elevation of the top of the two poles are respectively 60° and 30°. Find the distance of the point from the two poles.
Ans. Let the height of both poles is h and the point between them on the road is E
As per the figure
tan 60° = AB/BE =h/BE
√3 =h/BE
BE = h/√3……..(i)
tan 30° = DC/CE =h/CE
1/√3 = h/CE
CE = h√3….(ii)
CE = 80 – BE
From equation (i) and (ii)
h√3 = 80 -h/√3
h√3 +h/√3 =80
(3h +h)/√3 =80
4h/√3 =80
h = 80√3/4 =20√3
The height of both poles is 20√3 m
From equation (i)
CE =h√3 =20√3 ×√3 =60
The distances of one pole from the point is 60 m and from another pole is (80-60)=20m
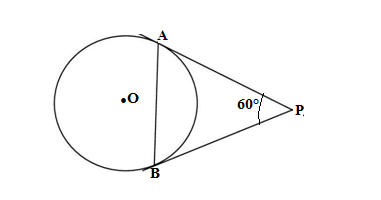
Q9.PA and PB are the tangents drawn to a circle with centre O. If PA= 6 cm and ∠ APB=60°, then find the length of the chord AB.
Ans. Considering the ΔAPB, ∠APB =60°(given)
PA and PB are the tangents drawn from an external point P are equal
PA = PB
∠ABP = ∠PAB (angles opposite to equal side are equal)
∠ABP +∠PAB+∠APB=180°
∠ABP +∠ABP+∠APB=180°
2∠ABP +60° = 180°
2∠ABP = 180° – 60° =120°
∠ABP = 120°/2 =60°
So,∠PAB =60°
Since ∠PAB=∠ABP =∠APB=60°
Therefore ΔAPB is an equilateral triangle
It implies that
AB =PA = 6 cm
Hence length of the chord is 6 cm
Q10.The sum of the squares of three positive numbers that are consecutive multiples of 5 is 725. Find the three numbers.
Ans.Let three consecutive multiples of 5 are 5x, 5x +5, 5x +10
It is given that sum of the squares of three positive numbers that are consecutive multiples of 5 is 725
∴ (5x)² +(5x +5)² +(5x +10)² =725
25x² +25x² +25 +50x +25x² +100 +100x=725
75x² +150x +125 – 725 =0
75x² +150x -600=0
x² +2x -8=0
x² +4x -2x-8=0
x(x +4) -2(x +4) =0
(x +4)(x -2) =0
x =-4,x =2
Since the numbers are positive,so neglecting the root x =-4,therefore taking x =2
The required positive numbers are
5x =5×2 =10,5x +5=5×2+5=15,5x +10=5×2+10=20
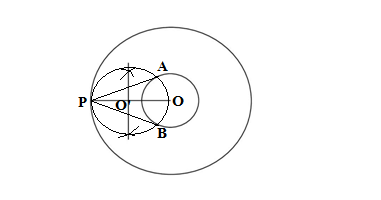
Q11.Construct two concentric circles of radii 3cm and 7cm. Draw two tangents to the smaller circle from a point P which lies on the bigger circle.
Ans. Steps of the construction:
(i) Drawing two concentric circles of radii 3cm and 7cm cenred at O
(ii) Drawing a radius OP of the larger circle.
(iii) Drawing the perpendicular bisector of OP which intersects OP at O’.
(iv)Drawing a circle of the radius PO’ with centre O’ which intersects the smaller circle at A and B.
(v) Drawing two tangents AP and BP.
AP and BP are the required tangents.
OR
Draw a pair of tangents to a circle of radius 6cm which are inclined to each other at an angle of 60°. Also find the length of the tangent.
Ans.
Steps of the construction:
(i) Drawing a circle of the radius 6 cm.
(ii)Drawing two radii OB and OC such that ∠BOC =120° (since ∠BAC +∠BOC =180°).
(iii) Drawing two perpendicular line on OB and OC from the point B and C,both of the perpendiculars meet each other at A.
AB and AC are the required tangents.
Q12.The following age wise chart of 300 passengers flying from Delhi to Pune is prepared by the Airlines staff.
Find the mean age of the passengers.
Ans.
| Age | No.of Passengers(f) | Class Mark(x) | fx |
| 0-10 | 14 | 5 | 70 |
| 10-20 | 44-14=30 | 15 | 450 |
| 20-30 | 82-44=38 | 25 | 950 |
| 30-40 | 134-82=52 | 35 | 1820 |
| 40-50 | 184-134=50 | 45 | 2250 |
| 50-60 | 245-184=61 | 55 | 3355 |
| 60-70 | 287-245=42 | 65 | 2730 |
| 70-80 | 300-287=13 | 75 | 975 |
| ∑f =300 | ∑fx=12600 |
Mean= ∑fx/∑f
=12600/300=42
Hence mean age of the passengers is 42 years
CASE STUDY I
Q13. A lighthouse is a tall tower with light near the top. These are often built on islands, coasts or on cliffs. Lighthouses on water surface act as a navigational aid to the mariners and send warning to boats and ships for dangers. Initially wood, coal would be used as illuminators. Gradually it was replaced by candles, lanterns, electric lights. Nowadays they are run by machines and remote monitoring.
Prongs Reef lighthouse of Mumbai was constructed in 1874-75. It is approximately 40 meters high and its beam can be seen at a distance of 30 kilometers. A ship and a boat are coming towards the lighthouse from opposite directions. Angles of depression of flashlight from opposite directions. Angles of depression of flashlight from the lighthouse to the boat and the ship are 30° and 60° respectively.
(i)Which of the two, boat or the ship is nearer to the lighthouse. Find its distance from the lighthouse?
Ans.Angles of depression = Angles of depression
∠ADB =30°, ∠ACB =60°
The height of the lighthouse(AB) is 40 meters
tan 30° =AB/DB, tan 60°=AB/BC
1/√3 = 40/DB, √3 = 40/BC
DB =40√3, BC =40/√3
The distance of the ship(BC) is nearer to the lighthouse and the distance of the ship from the lighthouse is 40/√3 =40/1.732=23.09 m
(ii)Find the time taken by the boat to reach the lighthouse if it is moving at the rate of 20 km per hour.
Ans. Time =distance/speed
The distance of the boat from the lighthouse is DB=40√3
Speed of the boat =20 km per hour.
Time is taken by the boat to reach the lighthouse
=40√3/20= 2√3 hour
Q14.Krishnanagar is a small town in Nadia District of West Bengal. Krishnanagar clay dolls are unique in their realism and quality of their finish. They are created by modelling coils of clay over a metal frame. The figures are painted in natural colours and their hair is made either by sheep’s wool or jute. Artisans make models starting from fruits, animals, God, goddess, farmer, fisherman, weavers to Donald Duck and present comic characters. These creations are displayed in different national and international museums
Here are a few images (not to scale) of some clay dolls of Krishnanagar
The ratio of diameters of red spherical apples in Doll-1 to that of spherical oranges in Doll-2 is 2:3. In Doll-3, male doll of blue colour has cylindrical body and a spherical head. The spherical head touches the cylindrical body. The radius of both the spherical head and the cylindrical body is 3cm and the height of the cylindrical body is 8cm. Based on the above information answer the following questions:
(i)What is the ratio of the surface areas of red spherical apples in Doll-1 to that of spherical oranges in Doll-2.?
Ans.It is given that the ratio of diameters of red spherical apples in Doll-1 to that of spherical oranges in Doll-2 is 2:3
Let the diameter of red spherical apples in Doll-1 is 2r and the diameter of spherical oranges in Doll-2 is 3r
Therefore radius of red spherical apples is 2r/2=r and radius of spherical oranges is 3r/2
Ratio of their surface areas =4πr²/4π(3r/2)²=4r²/9r²=4/9
Hence the ratio of surface areas of red spherical apples in Doll-1 to that of spherical oranges in Doll-2 is 4:9
(ii) The blue doll of Doll-3 is melted and its clay is used to make the cylindrical drum of Doll-4. If the radius of the drum is also 3cm, find the height of the drum
Ans. Since the blue doll of Doll-3 is melted and its clay is used to make the cylindrical drum of Doll-4
∴ The volume of the blue doll of Doll-3 = Volume of the cylindrical drum of Doll-4
The volume of spherical head +The volume of cylindrical body = Volume of the cylindrical drum of Doll-4
4/3×π×3³ +π×3²×8 = π×3²h (h=height of the cylindrical drum of Doll-4)
4/3 ×27 +9×8 =9h
4×9 +9×8 =9h
h = 4+8 =12
Hence the height of the cylindrical drum of doll -4 is 12 cm
You can compensate us by donating any amount of money for our survival
Our Paytm NO 9891436286
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions of class 9 science
CBSE Class 9-Question paper of science 2020 with solutions
CBSE Class 9-Sample paper of science
CBSE Class 9-Unsolved question paper of science 2019
NCERT Solutions of class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT solutions of class 10 science
Solutions of class 10 last years Science question papers
CBSE Class 10 – Question paper of science 2020 with solutions
CBSE class 10 -Latest sample paper of science
NCERT solutions of class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions of class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
