Solution of CBSE Class 10 Maths(Standard) Sample Paper for CBSE Board 2022 Term 2

Solution of CBSE Class 10 Maths(Standard) Sample Paper for CBSE Board 2022 Term 2 published by CBSE is created by an experienced maths expert for the help of CBSE class 10 in boosting their preparation of maths question paper CBSE Board exam term 2. Total questions in the class 10 maths sample paper for CBSE Board Term 2 are 14, which are divided into three sections A,B, and C. In section A there are 6 questions each of 2 marks, Section B comprises of 4 questions each of 3 marks and section C comprises of 4 questions each of 4 marks. Section A has two questions in which internal choice is provided, Section B and Section C both have been provided with an internal choice of one question each.
Solution of CBSE Class 10 Maths(Standard) Sample Paper for CBSE Board 2022 Term 2
Section-A
Q1.Find the value of a25-a15 for the AP: 6, 9, 12, 15, ………..
OR
If 7 times the seventh term of the AP is equal to 5 times the fifth term, then find the value of its 12th term.
Ans.The given AP is 6, 9, 12, 15, ………..
nth term of the AP is given by
an = a +(n -1)d
Where a =6,d = 9 -6 =3
a25 = 6+(25 -1)×3 =6+24×3 =6 +72=78
a15 = 6+(15 -1)×3 =6+14×3 =6 +42=48
a25 – a15 = 78 – 48 =30
OR
7×Seventh term of an AP = 5×Fifth term of the same AP
7[a +(7-1)d] = 5[a +(5-1)d]
7a + 7×6d =5a + 5×4d
7a + 42d =5a + 20d
7a – 5a = 20d -42d = -22d
2a = -22d
a = -11d
12th term of the AP is
a12 = -11d +(12 -1)d =-11d +11d =0
Q2.Find the value of m so that the quadratic equation mx(5x− 6) = 0 has two equal roots.
Ans. The quadratic equation ax² +bx +c =0 has equal roots when
D = b² – 4ac =0
The given quadratic equation
mx(5x− 6) = 0
5mx² – 6mx =0
b = -6m, a =5m and c =0
(-6m)² -4×5m×0 =0
36m² =0
m =0
Q3.From a point P, two tangents PA and PB are drawn to a circle C(0, r). If OP = 2r, then find ∠APB. What type of triangle is ΔAPB?
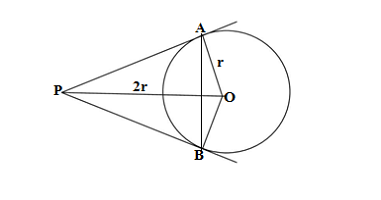
Ans.The line segment joining an external point to the centre of the circle bisects the angle between the tangents drawn from the same external point
∠APB=2∠APO
∠OAP =90° (the angle between the radius and the tangent)
Therefore ΔOAP is a right triangle where
OP=2r is the hypotenuse and OA =r is the perpendicular for the ∠APB under consideration
Let the ∠APB =θ°
sin θ° =p/h =r/2r =1/2
Since sin 30° =1/2
sin θ° = sin 30°
θ° = 30°
∠APB = 2θ° =2×30° =60°
Since the tangents drawn from an external point to the circle are equal
AP = PB moreover ∠APB =60°
∠APB +∠PAB +∠PBA =180°
60° + 2∠PAB = 180°[∠PAB =∠PBA]
2∠PAB = 180°-60°
∠PAB =120°/2 =60°
Therefore ΔAPB is an equilatral triangle
Q4.The curved surface area of a right circular cone is 12320 cm². If the radius of its base is 56cm, then find its height.
Ans. The given curved surface area of a right circular cone is 12320 cm²
Curved surface area of a right circular cone =πrl
where r =56 cm is given radius of the base and h is the height
Therefore
πrl= 12320
(22/7) ×56×l = 12320
l = (12320 ×7)(22×56) =12320/(22×8) =12320/176=70
Slant height,l =70 cm
Therefore height ,h=√(l² -r²) =√(70² -56²) =√(4900-3136) =√1764 =42 cm
Q5.Mrs. Garg recorded the marks obtained by her students in the following table. She calculated the modal marks of the students of the class as 45. While printing the data, a blank was left. Find the missing frequency in the table given below.
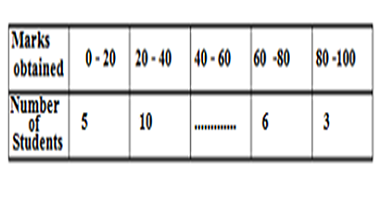
Ans.Let the missing frequency of the student is F

Since the mode of the data given to us is 45 which lies between (40 -60),therefore modal class is 40 – 60.
Where M =45,frequency preceded by the modal frequency(f0)=10
Modal frequency (f1) =F, frequency succeeded by the modal frequency(f2)=6,lower limit of the modal class,l=40
20 F -200 =10F – 80
20F -10F = -80 +200 =120
10F =120
F = 120/10 =12
Hence the missing frequency in the table is 12
Q6.If Ritu were younger by 5 years than what she really is, then the square of her age would have been 11 more than five times her present age. What is her present age?
OR
Solve for x: 9x² – 6px + (p² – q²) = 0
Ans. Let the present age of Ritu is x
If Ritu is 5 years younger than her present age then his age is =x -5
5 times of his present age = 5x
According to the condition that the square of her age would have been 11 more than five times her present age
(x-5) ²= 5x+11
x²-10x +25 = 5x +11
x² -10x -5x +25 -11 =0
x² -15x +14 =0
x² -14x-x +14 =0
x(x -14) -1(x -14) =0
(x -14) (x -1) =0
x =14,1
x =1 is impossible because the age of Ritu can’t be negative 5 years back
Her present age is 14 years.
OR
Solve for x: 9x² – 6px + (p² – q²) = 0
The given equation is
9x² – 6px + (p² – q²) = 0
Applying the quadratic equation formula for the solution of qudaratic equation ax² +bx +c =0
x =[-b±√(b² -4ac)]/2a
Where a =9, b=-6p, c = (p² – q²)
x =[6p±√{36p² -4×9 (p² – q²)}]/(2×9)
=[6p±√{36p² -4×9(p² – q²)}]/18
=[6p ±√{36p² -36 (p² – q²)}]/18
=[6p ±6√{p² -1 (p² – q²)]/18
=[6(p ±√[p² -p²+q²]/18
=(p ±q)/3
Hence the value of x is =(p ±q)/3
Solution of CBSE Class 10 Maths(Standard) Sample Paper for CBSE Board 2022 Term 2
Section-B
Q7.Following is the distribution of the long jump competition in which 250 students participated. Find the median distance jumped by the students. Interpret the median

Ans.

N = 250
N /2 =250 /2 =125th term lies in 2 -3 class interval therefore 2-3 is midiuan group
Where l =2, cf =120, f =62,h =3 -2 =1
Hence midiun distance jumped by the students is 2.0806 m
Interpretation of the median-It can be observed that 50 % students jumped over 2.0806 m and 50 % students jumped bellow 2.0806 m
Q8.Construct a pair of tangents to a circle of radius 4cm, which are inclined to each other at an angle of 60°.
Ans.

The angle between the tangents drawn from an external point to the circle is 60°
The sum of the angle between the radii and the angle between the tangents is 180°
The angle between the radii is 180°- 60°=120°
Construction: (i) Drawing a circle of the radius 4 cm
(ii) Drawing two radii OP and OR such that the angle between them is 120°
(iii) Drawing 90° angle at P and R such that PQ⊥OP and QR ⊥OR, which join each other at point Q.
(iv) The required tangents are PQ and QR inclined to each other at an angle of 60°
Q9.The distribution given below shows the runs scored by batsmen in one-day cricket matches. Find the mean number of runs.
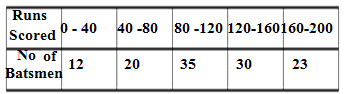
Ans.

Mean = A + ∑fd/∑f
= 100 +1280/120
=100 +10.67
=110.67
Hence the mean of the number of runs scored by the batsmen
Q10.Two vertical poles of different heights are standing 20m away from each other on the level ground. The angle of elevation of the top of the first pole from the foot of the second pole is 60° and the angle of elevation of the top of the second pole from the foot of the first pole is 30°. Find the difference between the heights of the two poles. (Take √3 = 1.73)
Ans. Let two poles are AB and DC

tan 60° = DC/BC
√3 = DC/20
DC= 20√3 m
tan 30° = AB/BC
1/√3 = AB/20
AB= 20/√3 m
DC – AB =20√3 -20/√3 =(60 -20)/√3=40/√3
Ratiolazing the denominator
(40√3)/(√3×√3)
=40√3/3 =(40×1.73)/3 =69.2/2 =23.06 m
The difference between the heights of the two poles is 34.6 m -11.53 m=23.04m
OR
A boy 1.7 m tall is standing on horizontal ground, 50 m away from a building. The angle of elevation of the top of the building from his eye is 60°. Calculate the height of the building. (Take √3 = 1.73)
Ans.Let the height of building is h

tan 60° = (h -1.7)/50
√3 = (h -1.7)/50
50√3 = h -1.7
h = 50√3 +1.7 =50×1.73 +1.7 =86.5+1.7=88.2 m
Solution of CBSE Class 10 Maths(Standard) Sample Paper for CBSE Board 2022 Term 2
Section-C
Q11.The internal and external radii of a spherical shell are 3cm and 5cm respectively. It is melted and recast into a solid cylinder of diameter 14cm, find the height of the cylinder. Also find the total surface area of the cylinder.
(Take π = 22/7)
Ans. The internal radius(r )of the spherical shell is given 3 cm
The outer radius(R )of the spherical shell is given 5 cm
The volume(V) of the spherical shell is
V= 4π/3(R³ -r³)
=4π(5³ -3³)/3
=4π(125 -27)/3
=4π×98/3
Since spherical shell is melted and recast into a solid cylinder
∴ Volume of the solid cylinder = Volume of the spherical shell
Diameter of the cylinder is given 14 cm therefore its radius R’ =14/2 =7 cm
πR’²h = 4π×98/3, where h is the height of the cylinder
R’²h =4π×98/3
7²h = 392/3
49h =392/3
h =392/(49×3)
h =8/3 m
Total srface area of the cylinder
=2πR'(R’ +h)
=2×22/7 ×7(7 +8/3)
=44(29/3)
=1276/3 m²
Q12.Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact to the centre.
Ans.Let there is a circle with centre O and two tangents PQ and QR are drawn from an external point Q

GIVEN: A circle with centre O and two tangents PQ and QR ,their points of contact to the circle are P and R are respectively
Construction: Joining O to P and O to R
TO PROVE: ∠PQR + ∠POQ =180°
PROOF: OP⊥PQ and OR⊥QR (radius is perpendicular to the tangent)
∴∠QRO = ∠QPO =90°
According to angle sum property of the quadrilateral OPQR
∠PQR + ∠POQ +∠QRO + ∠QPO =360°
∠PQR + ∠POQ +90°+90° =360°
∠PQR + ∠POQ +180°=360°
∠PQR + ∠POQ =360° – 180°
∠PQR + ∠POQ = 180°,Hence proved
OR
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ

GIVEN:Two tangents TP and TQ are drawn to a circle with centre O from an external point T
TO PROVE:∠PTQ = 2∠OPQ
PROOF:OP ⊥PT (radius is perpendicular to the tangent)
∴∠TPO =90°
PT = QT(tangents drawn to circle from an external point are equal)
∴∠TPQ = ∠TQP (opposite angles of equal sides in the Δ PTQ)
Applying angle sum property of the triangle
∠PTQ + ∠TPQ +∠TQP=180°
∠PTQ+ ∠TPQ +∠TPQ=180°
∠PTQ + 2∠TPQ =180°
∠TPQ =90°-∠OPQ
∠PTQ + 2(90°-∠OPQ)=180°
∠PTQ +180° -2∠OPQ = 180°
∠PTQ – 2∠OPQ =0
∠PTQ = 2∠OPQ, Hence proved
CASE STUDY -1
Q13.Trigonometry in the form of triangulation forms the basis of navigation, whether it is by land, sea or air. GPS a radio navigation system helps to locate our position on earth with the help of satellites.
A guard, stationed at the top of a 240m tower, observed an unidentified boat coming towards it. A clinometer or inclinometer is an instrument used for measuring angles or slopes(tilt). The guard used the clinometer to measure the angle of depression of the boat coming towards the lighthouse and found it to be 30°.

(i)Make a labelled figure on the basis of the given information and calculate the distance of the boat from the foot of the observation
Ans.Let the distance of the boat from the base of the tower is x m
The angle of the depression = The angle of the elevation = 30°

tan 30° = 240/x
1/√3 = 240/x
x = 240√3 m
(ii)After 10 minutes, the guard observed that the boat was approaching the tower and its distance from tower is reduced by 240(√3 – 1) m. He immediately raised the alarm. What was the new angle of depression of the boat from the top of the observation tower?
Ans.Let the new angle of depression of the boat from the top of the observation tower is θ after 10 minutes
After 10 minutes the distance of the boat is from the base of the tower is
=[ 240√3 -240(√3 – 1)]m
=240 m
The angle of the depression = The angle of the elevation = θ
tan θ =240/240
tan θ =1 =tan 45°
θ = 45°
CASE STUDY 2
Push-ups are a fast and effective exercise for building strength. These are helpful in almost all sports including athletics. While the push-up primarily targets the muscles of the chest, arms, and shoulders, support required from other muscles helps in toning up the whole body.

Nitesh wants to participate in the push-up challenge. He can currently make 3000 push-ups in one hour. But he wants to achieve a target of 3900 push-ups in 1 hour for which he practices regularly. With each day of practice, he is able to make 5 more push-ups in one hour as compared to the previous day. If on first day of practice he makes 3000 push-ups and continues to practice regularly till his target is achieved. Keeping the above situation in mind answer the following questions:
(i)Form an A.P representing the number of push-ups per day and hence find the minimum number of days he needs to practice before the day his goal is accomplished?
Ans.Let the number of days is n in which he achieves his target
Nitesh currently make 3000 push-ups in one hour
He is able to make 5 more push-ups in one hour as compared to the previous day
He wants to achieve a target of 3900 push-ups in 1 hour for a push-up challenge
The numbers of push up on first day,second day,third day and so on till he achieve 3900 push up per hour
Therefore the AP will be formed as follows
3000,3005,3010,…….3900
Where a =3000,d =5,an= 3900
The nth term of an AP is given as
an= a +(n -1)d
3900 = 3000 +(n -1)5
5n -5 = 900
5n =905
n =905/5 =181
Hence the minimum number of days is 181 he needs to practice to achieve his goal
(ii)Find the total number of push-ups performed by Nitesh up to the day his goal is achieved.
Ans. Total number of push-ups performed by Nitesh up to the day his goal is achieved=Sum of the AP
The AP of daily push up
3000,3005,3010,…….3900
Where a =3000,d =5,an= 3900 and n =181
The sum of n terms of an AP is given by
S = n/2[a +l]
Where n =181, a =3000, l =3900
S=181/2[3000 +3900]
=181/2[6900]
=181×3450=624450
Hence the total number of push-ups performed by Nitesh up to the day his goal is achieved is 624450
We hope you would have liked the Solution of the CBSE Class 10 Maths(Standard) Sample Paper for the CBSE Board 2022 Term 2 exam. If you want to get similar solutions of unsolved questions of assignment, sample papers, and question papers then you can send us the pdf or link of unsolved questions, we will publish the solutions on our website and create a Utube video, subsequently, it will reach to your mobile phone if you subscribe us.
You can compensate us by donating any amount of money for our survival
Our Paytm No 9891436286
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions for class 9 maths
NCERT Solutions for class 9 science
CBSE Class 9-Question paper of science 2020 with solutions
CBSE Class 9-Sample paper of science
CBSE Class 9-Unsolved question paper of science 2019
NCERT Solutions of class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for Class 10 Science
Solutions of class 10 last years Science question papers
CBSE Class 10 – Question paper of science 2020 with solutions
CBSE class 10 -Latest sample paper of science
Solution of CBSE Class 10 Maths(Standard) Sample Paper for CBSE Board 2022 Term 2Solutions-Class 10 Maths(Standard) sample paper Term 2 published by CBSE-2022 Board
NCERT solutions of class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions of class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |



