Class 10 Maths Solutions of Question Paper Set 4 Term 1 CBSE Board Exam 2021-22
Class 10 Maths Solutions of Question Paper Set 4 Term 1 CBSE Board Exam 2021-22 is created here for the students of 10 class so that they could examine their mistakes and correct them in next exam Term 2 CBSE Board 2021-22. Class 10 Maths Solutions of Question Paper Set 4 Term 1 CBSE Board Exam 2021-22 is helpful to clear your maths basic concepts.If you face any doubt in the Class 10 Maths Solutions of Question Paper Set 4 Term 1 CBSE Board Exam 2021-22 you are free to write on the comment box.
Class 10 Maths Solutions of Question Paper Set 4 Term 1 CBSE Board Exam 2021-22
Q1.The exponent of 5 in the prime factorization of 3750 is
(a) 3 (b) 4 (c) 5 (d) 6
Ans.(b) 4
3750 =54×3×2
Q2.The graph of a polynomial P(x) cuts the x -axis at 3 points and touches it at 2 other points. The number of zeroes of P(x) is
(a ) 1 (b) 2 (c) 3 (d) 5
Ans.(c) 3
Q3.The value of x and y satisfying the two equations 32 x + 33y = 34, 33x +32y = 31 respectively are :
(a) -1,2 (b) -1,4 (c) 1,-2 (d) -1,-4
Ans.(a) -1,2
The given equations are
32 x + 33y = 34…..(i) and 33x +32y = 31…….(ii)
Subtracting and adding both equations we get equation (iii) and equation (iv)
-x +y =3…..(iii) and 65x +65y =65⇒x +y =1….(iv)
Solving the equation (iii) and equation (iv),we get
y=2 and x =-1
Q4. If A(3,√3), B(0,0) and C(3,k) are the three vertices of an equilateral triangle ABC, then the value of k is
(a) 2 (b) -3 (c) -√3 (d)-√2
Ans.(c) -√3
Since ABC equilateral triangle
AB =BC =AC
√[(3-0)²+(√3-0)²] =√[(0-3)²+(0-k)²]
9 +3 =9 + k²
k = ±√3
AC =√[(3-3)²+(√3-k)²]
Putting k =√3
AC = 0, so canceling k=√3
Therefore value of k =-√3
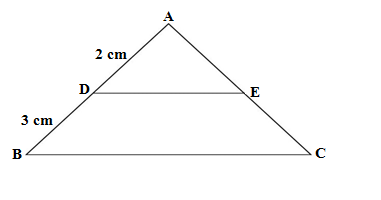
Q5. In figure ,DE ∥ BC , AD = 2 cm and BD = 3cm, then ar (ΔABC) : ar(ΔADE) is equal to
(a) 4 : 25 (b) 2 : 3 (c) 9 : 4 (d) 25 : 4
Ans. (d) 25 : 4
Considering ΔABC and ΔADE
Since in ΔABC and ΔADE, DE ∥ BC
∠ D = ∠ B (corresponding angles)
∠ E = ∠ C (corresponding angles)
ΔABC ∼ ΔADE(AA rule)
AD = 2 cm and AB =2 + 3 = 5cm
Q6. If cot θ = 1/√3, the value of sec²θ + cosec²θ is
sec²θ + cosec²θ
(1 + tan²θ) + (1 + cot²θ)
tan²θ + cot²θ + 2
We are given cot θ = 1/√3 ⇒tan θ =√3
(√3)² +(1/√3)² +2
3 + 1/3 +2 = (9+1+6)/3 =16/3
Q7.The area of quadrant of a circle where the circumference of circle is 176 m, is
(a) 2464 m² (b) 1232 m² (c) 616 m² (d) 308 m²
Ans.(c) 616 m²
The circumference of circle is = 176 m
circumference of circle=2πr
2πr = 176
2 ×22r/7 = 176
r=(176×7)/44 =28 m
Area of quadrant= πr²/4=(22/7)×28×28/4= 22×28 =616 m²
Q8.For an event E, ,then the value of x³-3 is
(a) -2 (b) 2 (c) 1 (d) -1
Ans.(a) -2
We know the probability of happening of an event + The probability of not happening of an event=1
We are given that
Therefore x =1
Hence the value of x³-3=1³-3 =1 -3 = -2
Q9.What is the greatest possible speed at which a girl can walk 95 m and 171 m in an exact number of minutes ?
(a)17 m/min (b) 19 m/min (c) 23 m/min (d) 13 m/min
Ans. (b) 19 m/min
The greatest possible speed at which a girl can walk 95 m and 171 m is= HCF of 95 and 171
95 =5×19
171=3²× 19
HCF(95,171) =19
Q10. In the figure, the graph of polynomial P(x) is shown. The number of zeroes of P(x) is
(a)1 (b) 2 (c) 3 (d) 4
Ans. (c) 3
P(x) is intersecting x axis at 3 points
Q11.Two lines are given to be parallel .The equations of one of the lines is 3x – 2y =5.The equation of the second line can be
(a) 9x + 8y = 7 (a)-12x – 8y = 7 (a) -12x + 8y = 7 (a)12x + 8y = 7
Ans: A pair of linear equations a1x +b1y +c1 and a2x +b2y +c2 are parallel when
a1/a2 = b1/b2≠c1/c2
In equations 3x – 2y =5 and -12x + 8y = 7
3/-12 = -2/8≠-5/-7
Therefore equations 3x – 2y =5 and -12x + 8y = 7 are parallel
Q12. Three vertices of a parallelogram ABCD are A(1,4), B(-2,3) and C(5,8). The ordinate of the fourth vertex D is
(a) 8 (b) 9 (c) 7 (d) 6
Ans.(b) 9
Let coordinates of fourth vertex D are (x,y) and both diagonals intersect at O
The given three vertices of a parallelogram ABCD are A(1,4), B(-2,3), and C(5,8)
In parallelogram ABCD ,AC and BD are diagonal
Since diagonal of a parallelogram bisect each other
O is the midpoint of AC as well as of BD
Mid point of AC =[(1 +5)/2, (4 +8)/2] =(3,6)
Mid point of BD =[(x -2)/2, (y +3)/2 ]
On comparing their ordinate,we have
(y +3)/2 = 6
y +3 = 12⇒y =9
Q13. In Δ ABC and ΔDEF ,∠F = ∠C, ∠B = ∠E and AB = (1/2) DE. Then, the two triangles are
(a) Congruent, but not similar.
(b) Similar, but not congruent.
(a) Neither congruent nor similar.
(a) Congruent as well as similar.
Ans.(b) Similar, but not congruent.
In Δ ABC and ΔDEF, ∠F = ∠C, ∠B = ∠E ⇒Δ ABC ∼ ΔDEF (AA rule)
AB = (1/2) DE ⇒ AB ≠ DE ⇒ Δ ABC is not congruent to ΔDEF
Q14.In Δ ABC right angled at B ,sin A = 7/25, then the value of cos C is
(a) 7/25 (b) 24/25 (c) 7/24 (d) 24/7
Ans. (b) 24/25
The given Δ ABC right angled at B
sin A = 7/25 = Perpendicular/Hypotenuse
Base = √(25² -7²) = √(625 -49)= √576 =24
cos C = Base/Hypotenuse=BC/AC =24/25
Q15.The minute hand of a clock is 84 cm long. The distance covered by the tip of the minute hand from 10:10 am to 10:25 am is
(a) 44 cm (b) 88 cm (c) 132 cm (d) 176 cm
Ans.(c) 132 cm
The length of minute hand = 84 cm
The distance covered by the tip of the minute hand from 10:10 am to 10:25 am is = Length of arc made by the tip of minute hand
Time duration from 10:10 am to 10:25 am is =15 minutes
Angle subtended by the arc ,θ= (15/60) ×360° =90°
The length of arc =(θ/360°)2πr = (90°/360°)×2×(22/7 )×84 =132
Q16. The probability that the drawn card from a pack of 52 cards is neither an ace nor a spade is
(a) 9/13 (b) 35/52 (c) 10/13 (a) 19/26
Ans. (b) 35/52
Toatal number of cards = 52
The number of ace cards =4
The number of spade cards=13
The number of cards which are neither an ace nor a spade =52 – (4 +13) =35
P( neither an ace nor a spade) = (number of cards neither an ace nor a spade)/ Toatal number of cards =35/52
Q17.Three alarm clocks ring their alarms at intervals of 20 min,25 min, and 30 min respectively. If they first beep together at 12 noon, at what time will they beep again for the first time ?
(a) 4 : 00 pm (b) 4 : 30 pm (c) 5 : 00 pm (a) 5 : 30 pm
Ans.(c) 5 : 00 pm
The given three alarm clocks ring in the intervals of 20 min,25 min, and 30 min
The beep together at 12 :00 noon
Three alarm clock beep together after after a time period equivant to the LCM of 20,25 and 30
20=2²×5
25 =5²
30 =2 ×3×5
LCM ( 20,25 , 30) = 2²×5²×3=300
300 minutes = 5 hour
Hence they will beep together at 12 : 00 +5h = 5:00 PM
Q18.A quadratic polynomial ,the product and sum of of whose zeroes are 5 and 8 respectively is
(a) k[x² -8x +5] (b) k[x² +8x +5] (a) k[x² -5x +8] (a) k[x² +5x +8]
Ans.(a) k[x² -8x +5]
A quadratic polynomial whose product and sum is given is computed by the following way
k(x² -(sum of zeroes)x + product of zeroes)
k(x² -8x +5),where k is a real number
Q19.Points A(-1,y) and B(5,7) lie on a circle with centre O(2,-3y). The values of y are
(a) 1,-7 (b) -1,7 (a) 2,7 (a) -2,-7
Ans. (b) -1,7
The given points on a circle are A(-1,y) and B(5,7) and centre O(2,-3y)
OA = OB (radii of the circle)
√[(-1-2)² + (y+3y)²] = √[(5-2)² + (7+3y)²]
9 + 16y² = 9 + 49 +9y² + 42y
7y² – 42y- 49 =0
y² – 6y- 7 =0
y² – 7y+y- 7 =0
y(y -7) +1(y -7) =0
(y -7)(y +1) =0⇒y =7 and y =-1
Q20.Given that sec θ = √2, the value of (1+tan θ)/sin θ is
(a) 2√2 (b) √2 (c) 3√2 (d) 2
Ans.(a) 2√2
We are given that
sec θ = √2⇒ sec θ = h/b =√2/1
p = √[(√2)²-1²] =√(2-1)=1
tan θ =p/b =1/1 =1
sin θ = p/h =1/√2
(1+tan θ)/sin θ = (1+1)/(1/√2) =2√2
Class 10 Maths Solutions of Question Paper (Standard) Term 1 CBSE Board Exam 2021-22
Section- C
Q21. The greatest number which when divides 1251,9377 and 15628 leaves remainders 1,2 and 3 respectively is
(a) 575 (b) 450 (c)750 (d) 625
Ans. 1251 -1=1250
9377 -1=9376
15628-1=15627
Q22. Which of the following cannot be the probability of an event
(a) 0.01 (b) 3% (c) 16/17 (d) 17/16
Ans. (a) 17/16
The value of probability ,P(E) of an event is
0 ≤ P(E) ≤ 1
17/16 > 1
So, 17/16 can not be the probability of an event
Q23.The diameter of a car wheel is 42 cm. The number of complete revolutions it will make in moving 132 km is
(a) 104 (b)105 (c)106 (d)103
Ans. (b)105
The given diameter of a car wheel is 42 cm
Rdius of the wheel =42/2 =21 cm
Circumference of the wheel= 2πr = 2×22/7 ×21= 132 cm
The distance covered by the wheel in one revolution = circumference of the wheel
Distance covered by the car= 132 km= 13200000 cm
The number of revolution = (distance covered by the car)/( circumference of the wheel)= 13200000 /132 =105
Q24.If θ is an acute angle and tan θ + cot θ =2, then the value of sin³θ + cos³θ is
(a) 1 (b) 1/2 (c)√2/2 (d) √2
Ans. (c)√2/2
The given equation is
tan θ + cot θ =2
Converting it into the terms of sin and cos
sin θ/cos θ +sin θ/cos θ =2
(sin²θ +cos²θ)/sin θ cos θ = 2
1/sin θ cos θ =2
sin θ cos θ = 1/2 …..(i) and sin²θ +cos²θ -2sin θ cos θ =0⇒(sin θ – cos θ)²=0⇒sin θ – cos θ=0……(ii)
From equation (ii) and (i)
(sin θ +cos θ)²=(sin θ – cos θ)² +4sin θ cos θ= 0 +4×1/2 =2
sin θ +cos θ = √2……(iii)
sin³θ + cos³θ = (sin θ +cos θ)(sin² θ +cos² θ-sinθ cosθ)
Putting the values from equation (i) and (iii)
sin³θ + cos³θ = √2(1 – 1/2) = √2/2
Q25. The ratio in which the line 3x + y -9 =0 divides the line segment joining the points (1,3) and (2,7) is
(a) 3 : 2 (a) 2 : 3 (a) 3 : 4 (a) 4 : 3
Ans.(a) 3 : 4
Let the given line 3x + y -9 =0 divides the line segment joining the points (1,3) and (2,7) into k : 1 and point of intersection is (a,b)
Applying section formula
Since (a,b) is point of intersection of line and line segment ,it must satisfy the equation of line
Therefore putting the value x =a and y =b
Multiplying by (k+1)
6k +3 +7k +3 -9k -9 =0
4k -3 =0
k = 3/4
Q26. If x -1 is a factor of the polynomial p(x) = x³ + ax² + 2b and a + b = 4, then
(a) a =5, b= -1 (b) a =9, b= -5 (c) a =7, b= -3 (d) a =3, b= 1
Ans. (b) a =9, b= -5
The given polynomial is p(x) = x³ + ax² + 2b
x -1 is the factor of p(x) ⇒ x =1 is one of the zeroes of p(x)
∴ 1³ + a(1)² +2b =0
a +2b = -1……(1)
The given equation is
a + b = 4 …..(ii)
Subtracting equation (ii) from equation (i)
b = -5
Putting the value of b in equation (ii)
a = 4 -b = 4 -(-5) = 9
Q27. If a and b are two coprime numbers, then a³ and b³ are
(a) Coprime (b) Not-coprime (c) Even (d) Odd
Ans.(a) Coprime
Let two co-prime numbers are 2 and 5
2³ and 5³ are also co-prime numbers ⇒ a³ and b³ are co-prime numbers
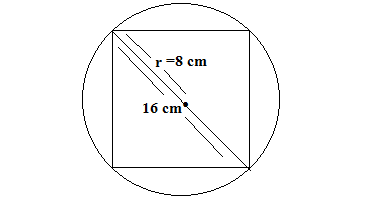
Q28. The area of a square that can be inscribed in a circle of area (1408)/7 cm² is
(a) 321 cm² (b) 642 cm² (c) 128 cm² (d) 256 cm²
Ans. (c) 128 cm²
The area of circle is given (1408)/7 cm²
πr² = (1408)/7 cm²
(22/7)r² = (1408)/7 cm²
r² = 1408/22 =64
r = 8
The diagonal of square is = 2×8 = 16 cm
side ² + side² = 16²
2side ²= 256
side ² = 128
Area of square = 128 cm²
Q29. If A(4,-2),B(7,-2) and C(7,9) are the vertices of a Δ ABC , then Δ ABC is
(a) equilateral triangle
(b) isoscell triangle
(c) right angle triangle
(d)isosceles right-angled triangle
Ans. (c) right angle triangle
Applying the distance formula for getting the length of sides
AB = √[(4-7)² +(-2 +2)²]=3
BC=√[(7-7)² +(-2 -9)²]=11
AC =√[(4-7)² +(-2 -9)²]=√(130)
AC² = 130, AB² =9 and BC² =121
AC² = AB² + BC² ⇒130 =9 +121
∴ Δ ABC is a right triangle with ∠B =90°
Q30. If α ,β are the zeroes of the quadratic polynomial p(x) =x² -(k+6)x+2(2k-1),then the value of k, if α +β= (1/2) α β,is
(a) -7 (b) 7 (c) -3 (d) 3
Ans. (b) 7
The given α ,β are the zeroes of the quadratic polynomial p(x) =x² -(k+6)x+2(2k-1)
It is given to us
α +β= (1/2) α β
α +β = -B/A = k+6 and α β =C/A =2(2k-1)
∴k+6 = (1/2)2(2k-1)=2k -1
-k = -7 ⇒ k =7
Q31.If n is a natural number ,then 2(5n + 6n ) always ends with
(a) 1 (b) 4 (c) 3 (d) 2
Ans.(d) 2
The given expression is 2(5n + 6n ), where n ∈ natural number
2(5n + 6n ),putting n=1,2,3…
2(51 + 6 1)=22, 2(52 + 6 2)= 122 and so on
The numbers end at 2
Q32. The line segment joining the points P(-3,2) and Q(5,7) is divided by the y -axis in the ratio
(a) 3 : 1 (b) 3 : 4 (c) 3 : 2 (d) 3 : 5
Ans. (d) 3 : 5
Let the line segment joining the points P(-3,2) and Q(5,7) is divided by the y-axis is the ratio of k: 1 and the point of intersection on the y-axis is (0,y)
Applying the section formula
0= (5k-3)/(k+1)
5k-3 =0 ⇒ k =3/5
Q33. If a cot θ + b cosec θ =p and b cot θ + a cosec θ =q, then p² – q² =
(a) a² – b² (b) b² – a² (c) a² + b² (d) b – a
Ans. (b) b² – a²
The given equations are
a cot θ + b cosec θ =p and b cot θ + a cosec θ =q
p² – q² =(a cot θ + b cosec θ )² – (b cot θ + a cosec θ)²
= a² cot² θ + b² cosec² θ + 2ab cot θ.cosec θ-b² cot² θ -a² cosec² θ- 2ab cot θ.cosec θ
=a²(cosec²θ-1) +b² (1+cot² θ ) + 2ab cot θ.cosec θ-b² cot² θ -a² cosec² θ- 2ab cot θ.cosec θ
=a²cosec²θ – a² +b² + b²cot²θ + 2ab cot θ.cosec θ-b² cot² θ -a² cosec² θ- 2ab cot θ.cosec θ
= b² – a²
Q34.If the parimeter of a circle is half to that of a square ,then the ratio of the area of the circle to the area of the square is
(a) 22 : 7 (b)11 : 7 (c) 7 : 11 (d)7 : 22
Ans. (d)7 : 22
It is given to us
Perimeter of the circle = Perimeter of the square/2
2πr = 4a/2 (r radius of the circle and a is side of the square)
2 ×(22/7)r = 2a
r/a = 7/22
The ratio between area of the circle to the area of the square is
πr²/a² =(22/7)(7/22)² =7 : 22
Q35. A dice is rolled twice . The probability that 5 will not come up either time is
(a) 11/36 (b) 1/3 (c) 13/36 (d) 25/36
Ans. (d) 25/36
Total outcomes when a dice is thrown twice =6² =36
The outcomes that 5 come up either time are (1,5),(2,5),(3,5),(4,5),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6) and (6,5)
The number of outcomes that 5 will not come up either time are =36 -11 =25
P(5 will not come up either time) =number of outcomes that 5 will not come up either tim/Total outcomes =25/36
Q36.The LCM of two numbers is 2400. Which of the following can not be their HCF?
(a) 300 (b) 400 (c) 500 (d) 600
Ans.(c) 500
The given LCM of two numbers is = 2400
LCM 2400 is undvisible by 500
Q37. In fig.PA, QB and RC are each perpendicular to AC .If x =8 cm and z = 6 cm,then y is equal to
(a) 56/7 cm (b) 7/56 cm (c) 25/7 cm (d) 24/7 cm
Ans. It is given that
PA, QB and RC are each perpendiculars to AC
∴ PA ∥ QB ∥ QB (perpendiculars on the same line AC)
In Δ APC and ΔQBC
∠PAC= ∠QBC=90° ( PA⊥AC,QB⊥AC)
∠QCB = ∠PCA
Δ APC ∼ ΔBQC (AA rule)
∴x/y = AC/BC
y/x = BC/AC….(i)
In Δ ARC and ΔAQB
∠ACR= ∠ABQ=90° (CR⊥AC,QB⊥AC)
∠ARC = ∠AQB
Δ ARC∼ ΔAQB(AA rule)
y/z = AB/AC…….(ii)
Adding both equations
y/x + y/z = BC/AC + AB/AC = (BC +AB)/AC =AC/AC =1
(yz +xy)/xz =1
(6y +8y)/(8×6) = 1
14y =48
y = 48/14 =24/7 cm
Q38. In ΔABC ,∠A =x°, ∠B =(3x -2°), ∠C=y°. Also ∠C – ∠B=9°. The sum of the greatest and the smallest angles of this triangle is
(a)107° (b)135° (c)155° (d)145°
Ans.(a)107°
In given ΔABC, ∠A =x°and ∠B =(3x -2°), ∠C=y°. Also ∠C – ∠B=9°
Substituting ∠C=y° and ∠B =(3x -2°) in ∠C – ∠B=9°
∠C – ∠B=9° (given)
y° – 3x + 2° =9°
y° – 3x = 9-2
y° – 3x =7….(i)
∠A +∠B +∠C = 180 (angle sum property of the triangle)
x + 3x -2 +y =180
4x +y = 182……..(ii)
Substracting equation (ii) from (i)
-7x =-175
x = 25
Putting the value of x =25 in equation (i)
y-3×25 =7
y= 7 +75 = 82
∠A =25°, ∠B =3×25-2 =75 -2 =73°, ∠C =82
The sum of the greatest and the smallest angles =25° +82° =107°
Q39.If secθ + tanθ = p, then tan θ is
(a) (p²+1)/2p (b) (p²-1)/2p (c) (p²-1)/ (p²+1) (d) (p²+1)/ (p²-1)
Ans.(b) (p²-1)/2p
The given equation is
secθ + tanθ = p
secθ = p – tan θ
Squaring both sides
sec²θ = p²+tan²θ-2p tanθ
1 + tan²θ = p²+tan²θ-2p tanθ
1 = p² – 2p tanθ
2p tanθ = p² – 1
tanθ = (p² – 1)/2p
Q40.The base BC of an equilateral ΔABC lies on the y-axis . The coordinates of C are (0, -3). If the origin is the mid-point of the base BC ,what are the coordinates of A and B ?
(a) A(√3,0),B(0,3) (b) A(±3√3,0),B(0,3) (c) A(±3√3,0),B(0,3) (d) A(-√3,0),B(0,3)
Ans. (b) A(±3√3,0),B(0,3)
The base BC of an equilateral ΔABC lies on the y-axis
Coordinates of C are (0, -3)
Let the coordinates of B are (a,b) and of A are (c,d)
Mid point of BC is given ,originO(0,0)
∴ (0+a)/2, (-3+b)/2 =(0,0)
Comparing LHS and RHS
a =0 and b =3
Hence coordinates of B are (0,3)
The length of BC =√[(0-0)²+(-3-3)²] =6 units
∴ BC = AB =AC =6units
Finding the altitude OA
OA =√[(6²-(6/2)²]=√(36-9) = √27 =3√3
OA can be either side of y-axis,so coordinates of A are (±3√3, 0)
Coordinates of B are (0, 3)
Q.No. 41-45 are based on Case Study -I, you have to answer any (4) four questions .Q.No. 46-50 are based on Case Study -II,you have to answer any (4) four questions.
Case Study-I
A book store shopkeeper gives a book on rent for reading .He has variety of books in his store related to fiction ,stories and quizzes etc.He takes a fixed charge for the first two days and an additional charge for the subsequent days.Amruta paid Rs 22 for a book and kept for 6 days ; while Radhika paid Rs 16 for keeping the book for 4 days.
Assume that the fixed charge be Rs x and the additional charge (per day) be Rs y.
Based on the above information ,answer any four of the following questions:
Q41.The situation of amount paid by Radhika ,is algebrically represented by
(a) x – 4y =16 (b) x + 4y =16 (c) x – 2y =16 (d) x + 2y =16
Ans. (d) x + 2y =16
Fixed charge of keeping the book =Rs x and additional charge =Rs y
Rdhika’s charge of 4 days for the books = Fixed charge(i.e 2 days) + additional charge (per day) for remaining 2 days =x +2y
16 =x +2y
Q42.The situation of amount paid by Amruta ,is algebrically represented by
(a) x – 2y =11 (b) x – 2y =22 (c) x+ 4y =22 (d) x – 4y =11
Ans. (c) x+ 4y =22
Fixed charge of keeping the book =Rs x and additional charge =Rs y
Amruta’s charge of 6 days for the books = Fixed charge(i.e 2 days) + additional charge (per day) for remaining 4 days =x +4y
22 =x +4y
Q43. What are the fixed charges for a book?
(a) Rs 9 (a) Rs 10 (a) Rs 13 (a) Rs 15
Ans. (a) Rs 10
The linear equations,we have
x+ 4y =22……(i) and x + 2y =16……(ii)
Substituting y=(22-x)/4 from (i) in equation (ii)
x + 2×(22-x)/4=16
x -x/2 =16 -11 = 5
x/2 = 5⇒ x =10
Q44. What are the additional charges for each subsequent day for a book?
(a) Rs 6 (b) Rs 5 (c) Rs 4 (d) Rs 3
Ans. (d) Rs 3
Putting the value of x =10 in equation (i)
10+ 4y =22
4y = 12⇒y =3
Q45. What is the total amount paid by both, if both of them have kept the book for 2 more days?
(a) Rs.35 (b) Rs. 52 (c) Rs. 50 (d) Rs. 58
Ans.(c) Rs. 50
Amruta already kept the book for 6 days and Radhika kept for 4 days
The total amount paid by both, if both of them have kept the book for 2 more days =2×Fixed charge(for 2 days)+remaining 6 days of Amruta +remaining 4 days of Radhika =2×10 +6×3 +4×3 = 20 +18 +12=50
Case Study -II
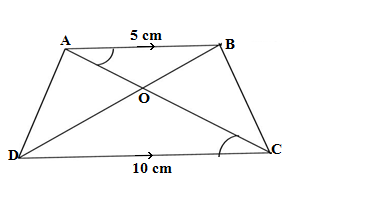
A farmer has a field in the shape of a trapezium, whose map with a scale 1 cm =20 m,is given below:
The field is divided into four parts by joining the opposite vertices.
Based on the above information, answer any four of the following questions:
Q46. The two triangular regions AOB and COD are
(a)Similar by AA criterion (b)Similar by SAS criterion (c) Similar by RHS criterion (d) Not similar
Ans.(a)Similar by AA criterion
In ΔAOB and ΔCOD
From the figure
∠OAB =∠OCD (alt.angle)
∠ABO =∠ODC (alt.angle)
ΔAOB ∼ ΔCOD(AA rule )
Q47. The ratio of the area of the ΔAOB to the area of ΔCOD, is
(a) 4 : 1 (b) 1 : 4 (c) 1 : 2 (d) 2 : 1
Ans.(b) 1 : 4
arΔAOB/arΔCOD = (AB/DC)²=(5/10)²=1/4
Q48. If the ratio of the parimeter of ΔAOB to the perimeter of ΔCOD would have been 1 : 4, then
(a) AB=2CD (b) AB=4CD (c) CD=2AB (d) CD=4AB
Ans. (d) CD=4AB
If two tiangles are similar, ΔAOB ∼ ΔCOD, then
AO/CO = OB/OD = AB/CD = (AO+OB+AB)/(CO +OD +CD)=1/4
Taking
AB/CD = 1/4
4AB =CD
Q49. If in Δ’s AOD and BOC, AO/BC = AD/BO =OD/OC, then
(a) ΔAOD ∼ ΔBOC (b) ΔAOD ∼ ΔBCO (c) ΔADO ∼ ΔBCO (d) ΔODA ∼ ΔOBC
Ans.(c) ΔADO ∼ ΔBCO
It is given that, in ΔAOD and BOC, AO/BC = AD/BO =OD/OC
The given (SSS) criteria is matched when ΔADO ∼ ΔBCO
Q50.If the ratio of areas of two similar triangles AOB and COD is 1 : 4, then which of the following statements is true ?
(a) The ratio of their perimeters is 3 : 4
(b) The corresponding altitudes have a ratio 1 : 2
(c) The medians have a ratio 1 : 4
(d) The angle bisectors have a ratio 1 : 16
Ans.(b) The corresponding altitudes have a ratio 1 : 2
We know the relationship between two similar triangles
arAOB/ar COD =AO²/CO² =OB²/OD² =AB²/DC² =1/4
AO²/CO²=1/4
AO/CO=1/2
The ratio between their parameter is 1/2
The ratio between their corresponding altitude is also 1:2
Medians also have the same ratio of 1:2
You can compensate us by donating any amount of money for our survival
Our Paytm No 9891436286
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions of class 9 maths
| Chapter 1- Number System | Chapter 9-Areas of parallelogram and triangles |
| Chapter 2-Polynomial | Chapter 10-Circles |
| Chapter 3- Coordinate Geometry | Chapter 11-Construction |
| Chapter 4- Linear equations in two variables | Chapter 12-Heron’s Formula |
| Chapter 5- Introduction to Euclid’s Geometry | Chapter 13-Surface Areas and Volumes |
| Chapter 6-Lines and Angles | Chapter 14-Statistics |
| Chapter 7-Triangles | Chapter 15-Probability |
| Chapter 8- Quadrilateral |
NCERT Solutions of class 9 science
CBSE Class 9-Question paper of science 2020 with solutions
CBSE Class 9-Sample paper of science
CBSE Class 9-Unsolved question paper of science 2019
NCERT Solutions of class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT solutions of class 10 science
Solutions of class 10 last years Science question papers
CBSE Class 10 – Question paper of science 2020 with solutions
CBSE class 10 -Latest sample paper of science
NCERT solutions of class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions of class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |