Class 9 Maths MCQs on Chapter 10-Circle with Solutions

Class 9 Maths MCQs on Chapter 10-Circle with Solutions are very important input study material for class 9 students of CBSE. Chapter 10-circle is the part of the maths syllabus in the CBSE Term 2 exam 2021-22 since 50 percent of total questions in CBSE Term 2 exam 2021-22 would be MCQs therefore students of class 9 are required to study the concerning article for achieving excellent marks.Here in Future Study Point you can study NCERT solutions of science and maths, sample papers, last year’s question papers with solutions, carrier guidance, and our articles on science and maths.
Class 9 Maths MCQs on Chapter 10-Circle with Solutions
Q1.The radius of a circle is 25 cm and the length of one of its chords is 14 cm. The distance of the chord from the centre is
(a) 12.5 cm (b) 13 cm (c) 7 cm (d) 24 cm
Ans. The given radius of the circle is 25 cm and chord 14 cm
The distance of the chord from the centre is perpendicular to the chord from the centre which bisects the chord
Therefore
The distance of the chord from the centre =√(25² -7²) = √(625 -49)= √576= 24 cm
Q2.A chord is at a distance of 12 cm from the centre of a circle of radius 13 cm. The length of the chord is
(a) 12 cm (b) 13 cm (c) 10 cm (d) 26 cm
Ans.The given radius of the circle is 13 cm and the distance of chord from the centre of the circle is 12 cm
The distance of the chord from the centre bisects the chord
Therefore
Length of chord/2 =√(13² -12²) = √(169 -144)= √25= 5 cm
Length of chord = 2×5 = 10 cm
Q3.In the given figure, POQ is a diameter of a circle and PR = QR. Then, ∠QPR=

(a) 60° (b) 50° (c) 40° (d) 45°
Ans.POQ is the given diameter
∠QRP = 90° (angle made on the semi-circle)
Since we are given
PR = QR
Therefore
∠PQR = ∠QPR (opposite angles of equal sides in a Δ)
∠QRP + ∠PQR +∠QPR =180°(angle sum property of Δ)
∠QPR + ∠PQR +∠QPR =180°
2∠QPR + 90° = 180°
2∠QPR = 90°
∠QPR = 45°
Q4.In the given figure, O is the centre of a circle. If ∠OPQ = 30° and R is a point on the circle, then ∠QRP =
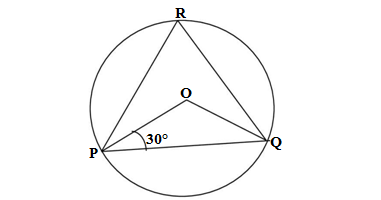
(a) 60° (b) 50° (c) 30° (d) 55°
Ans. The given ∠OPQ = 30° in ΔPOQ
OP = OQ (radii of the circle)
∴∠OPQ =∠OQP= 30° (opposite angles of equal sides in a Δ)
∠OPQ + ∠OQP +∠POQ =180°(angle sum property of Δ)
∠OPQ + ∠OPQ +∠POQ = 180°
2 ∠OPQ +∠POQ = 180°
2 ×30° +∠POQ= 180°
∠POQ = 180°- 60°= 120°
∠PRQ = ∠POQ/2 =120°/2 = 60°
Q5.An equilateral triangle of side 9 cm is inscribed a circle. The radius of the circle is
(a) 4.5 cm (b) 5 cm (c) 9 cm (d) 3√3 cm
Ans. The side of the given equilateral triangle is 9 cm
Let the centre of the circle is O and the equilateral triangle is ΔABC,O will also be the centre of the equilateral triangle.
Drawing OD ⊥BC
OD bisects BC (The perpendicular from the centre to chord bisects the chord)
Joining O to A,therefore AD will also bisects BC
ΔABD is a right triangle in which AB = 9 cm,BD =9/2 =4.5 cm
∴ AD =√(AB² -BD²) = √(9² -(9/2)²)=√(81 -81/4) =√[(324-81)/4] =√[243/4] =9√3/2 cm
OA = (2/3)AD (centre of the triangle divides its median into the 2 : 1)
OA = (2/3)× 9√3/2 = 9/√3 = 9√3/3 = 3√3 cm
Q6.In figure, O is the centre of a circle and ∠AOB = 130°, then ∠ACB =
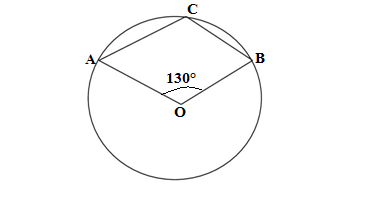
(a) 130° (b) 140° (c) 145° (d) 115°
Ans. In fig. it is given that ∠AOB = 130°
Ext.∠AOB = 360° – 130° = 230°
The ext.∠AOB and ∠ACB are the angles made by the same arc ACB
∴∠ACB = Ext.∠AOB/2 = 230°/2 = 115°
Q7.In figure, sides AB and AD of a quadrilateral ABCD are produced to E and F respectively. If ∠CBE = 100°, then find ∠CDF.

(a) 100° (b) 80° (c) 90° (d) 95°
Ans.From the figure
∠CBE = 100°
∠CBA=180°-∠CBE(linear pair)
∠CBA=180°-100°= 80°
∠CBA + ∠ADC = 180°(opposite angles of cyclic quadrilateral)
80° +∠ADC= 180°
∠ADC = 180°- 80° = 100°
∠CDF = 180°-∠ADC(linear pair)
∠CDF = 180°-100°= 80°
Q8.In the given figure, ABCD is the cyclic quadrilateral in which BC = CD and ∠CBD = 35°. Then, ∠BAD =

(a) 100° (b) 80° (c) 90° (d) 95°
Ans.We are given that ∠CBD = 35° and BC = CD
∠CBD = ∠CDB (opposite angles of equal sides in a Δ)
2∠CBD +∠BCD =180°(angle sum property of the Δ)
2×30°+∠BCD =180°
∠BCD = 180° – 60°= 120°
∠BCD + ∠BAD = 180°(opposite angles of cyclic quadrilateral)
∠BAD = 180°-∠BCD = 180°-120°= 60°
Q9.If the circumference of a circle is twice of its area then find its radius.
(a) 2 units (b) 1 unit (c) 3 units (d) 4 units
Ans. (b) 1 unit
Let the radius of the circle is r
Circumference of the circle is =2πr
Area of the circle is = πr²
As per the question
2πr = 2(πr²)
r = 1
Q10.The longest chord of the circle is
(a) Radius (b) Diameter (c) Arc (d) Segment
Ans.(b) Diameter
Q11. Two chords AB = 8 cm and BC =8 cm are drawn on a circle,if ∠AOB =60° then find ∠BOC .
(a) 120° (b) 60° (c) 40° (d) 30°
Ans.(b) 60°
Two chords given on a circle are AB = BC= 8 cm
Since we are given ∠AOB = 60°
∠AOB = ∠BOC =60°(equal chords subtends equal angles in a circle)
Q12. In two congruent circles of centres O , P ,if two equal chords AB and QR are drawn on them respectively such that ∠AOB =40° then
(a) ∠OAB=60° (b) ∠QPR=70° (c) ∠PQR=70° (d)∠OBA= 40°
Ans. In ΔAOB and ΔPQR
AO = PQ(radii of congruent triangles)
OB = PR(radii of congruent triangles)
AB = QR( given)
ΔAOB ≅ ΔQPR (SSS rule)
∠OAB = ∠PQR
In ΔAOB
∠AOB= 40° (given)
∠OAB = ∠OBA (since OA = OB)
∠OAB +∠OBA +∠AOB = 180°
2∠OAB = 180° – ∠AOB = 180° – 40° = 140°
∠OAB = 140°/2 = 70°
∠PQR=∠OAB =70°
Q13. PQ is the diameter of a circle and PR is the chord,if PQ = 26 cm and PR =24 cm then the distance of the chord PR from the centre is
(a) 2 cm (b) 5 cm (c) 3 cm (d) 4 cm
Ans.(b) 5 cm
It is given that PQ = 26 cm and PR =24 cm
Drawing the distance of the chord PR from the centre is OM ⊥PR

Since the distance OM ⊥ PR
∴ PM = PR/2 = 24/2 = 12 cm (perpendicular drawn from the centre to chord bisects the chord)
OP = diameter/2 =26/2 = 13 cm
ΔPOM is a right triangle
OM = √(PO² – PM²) = √(13² – 12²) =√(169 -144) =√25 = 5 cm
Therefore distance of the chord PR from the centre is 5 cm
Q14.In the given figure, AB is a chord of a circle with centre O and AB is produced to C such that BC = OB. Also, CO is joined and produced to meet the circle in D. If ∠ACD = 25°, then ∠AOD =

(a) 40° (b) 50° (c) 60° (d) 75°
Ans. (d) 75°
Since it is given to us
BC = OB.
∠BOC = ∠BCO =25° (opposite angles of equal sides in a Δ)
∠OBC = 180° – (25° +25°) = 180° -50° = 130°(angle sum property of the triangle)
∠ABO = 180° -130°= 50°(linear pair)
Since OA =OB (radii of the circle)
∴∠OAB = ∠ABO =50°(opposite angles of equal sides in a Δ)
∠AOD = ∠OAC +∠ACD (exterior angle property of the triangle)
∠AOD = 50°+25°= 75°
Q15.In the given figure, PQ is a chord of a circle with centre O and QOR is a diameter. If OS ⊥ PQ such that OS = 6 cm, then PR =
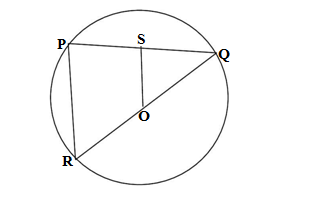
(a) 5 cm (b) 6 cm (c) 8 cm (d) 12 cm
Ans. (d) 12 cm
In ΔPQR and ΔSQO
∠QPR = 90° (angle made on semicircle since QOR is a diameter)
OS ⊥ PQ(given)
∴QSO = 90°
Considering ΔPQR and ΔSQO
∠Q = ∠Q
∠QPR = ∠QSO = 90°
ΔPQR ∼ SQO (AA rule)
OS/PR = OQ/QR
Since OQ is radius and QR is the diameter,therefore QR =2OQ
OS = 6 cm (given)
6/PR = OQ/2OQ =1/2
PR = 6 ×2 = 12 cm
Q16.In the given figure, O is the centre of a circle. If ∠AOB = =100° and ∠AOC = 90°, then ∠BAC =

(a) 85° (b) 95° (c) 75° (d) 85°
Ans.(d) 85°
We are given that
∠AOB = =100° and ∠AOC = 90°
Considering ΔAOC and ΔAOB
OA = OB and OA = OC (radii of circle)
∠ABO = ∠BAO and ∠CAO =∠ACO (opposite angles of equal sides in a Δ)
Applying angle sum property of the triangle
2∠BAO +100°= 180° and 2∠CAO+90°= 180°
∠BAO = 40° and ∠CAO = 45°
∠BAC = ∠BAO + ∠CAO =40° +45° = 85°
Q17.In the given figure, O is the centre of a circle and ∠AOC = 120°. Then, ∠BDC =

(a) 30° (b) 60° (c) 15° (d) 40°
Ans.(a) 30°
The given angle is
∠AOC = 120°
∠BOC = 180°-∠AOC (linear pair)
∠BOC = 180°-120° = 60°
∠BDC = ∠BOC /2 (angle subtended at the circle is half of the angle subtended at the centre by the same arc BC)
∠BDC = 60° /2 = 30°
Q18.In the given figure, O is the centre of a circle in which ∠OAB = 20° and ∠OCB = 50°. Then, ∠AOC =

(a) 30° (b) 60° (c) 15° (d) 40°
Ans.(b) 60°
The given angles are
∠OAB = 20° and ∠OCB = 50°
In ΔAOB
OA = OB (radii of the same circle)
∠OAB = ∠OBA = 20° (opposite angles of equal sides in a Δ)
In ΔBOC
OC = OB (radii of the same circle)
∠OCB = ∠OBC = 50° (opposite angles of equal sides in a Δ)
∠ABC = ∠OBC -∠OBA = 50° – 20° = 30°
∠AOC = 2∠ABC (angle subtended at the circle is half of the angle subtended at the centre by the same arc AC)
∠AOC = 2×30° = 60°
Q19.In the given figure, POQ is a diameter of a circle and PS = QS. Then, ∠QPS =

(a) 40° (b) 60° (c) 45° (d) 50°
Ans.(c) 45°
We are given that POQ is a diameter of a circle and PS = QS
In ΔPQS
∠QSP = 90°(angle made on the semicircle)
∠QPS = ∠PQS (opposite angles of equal sides in a Δ)
2∠QPS + ∠QSP = 180°
2∠QPS + 90° = 180°
2∠QPS = 90°
∠QPS = 45°
Q20.In the given figure, O is the centre of a circle. If ∠OAB = 40° and C is a point on the circle, then ∠ACB =

(a) 40° (b) 60° (c) 45° (d) 50°
Ans.(d) 50°
In ΔAOB the given angle is
∠BAO = 40°
AO = BO (radii of the circle)
∠BAO =∠ABO=40° (opposite angles of equal sides in a Δ)
∠BAO +∠ABO+∠AOB=180°
2×40°+∠AOB=180°
∠AOB = 180° – 80° = 100°
∠ACB = ∠AOB/2(angle subtended at the circle is half of the angle subtended at the centre by the same arc AB)
∠ACB = 100°/2 = 50°
We expect that you would have liked Class 9 Maths MCQs on Chapter 10-Circle with Solutions ,it is dam sure that these solutions of MCQ questions are going to help you in CBSE Board Term 2 exam 2021-22. As it is planned by CBSE that 50 percent questions of total questions in maths question paper of Term 2 would be of MCQ type so it is mandatory to solve these type of questions in a time slot in order to save time for doing descriptive questions in the question paper.If you liked this post of Class 9 Maths MCQs on Chapter 10-Circle with Solutions then don’t forget to subscribe our website and Utube channel.
You can compensate us by donating any amount of money for our survival
Our Paytm No 9891436286
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions of class 9 maths
| Chapter 1- Number System | Chapter 9-Areas of parallelogram and triangles |
| Chapter 2-Polynomial | Chapter 10-Circles |
| Chapter 3- Coordinate Geometry | Chapter 11-Construction |
| Chapter 4- Linear equations in two variables | Chapter 12-Heron’s Formula |
| Chapter 5- Introduction to Euclid’s Geometry | Chapter 13-Surface Areas and Volumes |
| Chapter 6-Lines and Angles | Chapter 14-Statistics |
| Chapter 7-Triangles | Chapter 15-Probability |
| Chapter 8- Quadrilateral |
NCERT Solutions of class 9 science
CBSE Class 9-Question paper of science 2020 with solutions
CBSE Class 9-Sample paper of science
CBSE Class 9-Unsolved question paper of science 2019
NCERT Solutions of class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT solutions of class 10 science
Solutions of class 10 last years Science question papers
CBSE Class 10 – Question paper of science 2020 with solutions
CBSE class 10 -Latest sample paper of science
NCERT solutions of class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions of class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |



