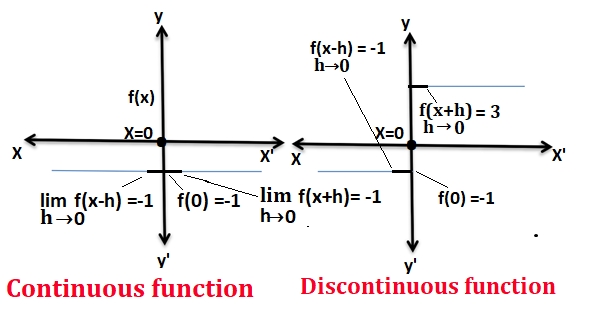
The continuity and differentiability of a function is always be determined at a point, Let there is a function f(x) = -1 which is drawn graphically as shown in the first figure, f(x) is continuous and differentiable at x =0 , f(x) is differentiable at x =0 because f ‘(x) =0,f(x) is a continuous function as well as a differentiable function at x=0,f(x) is continuous at x =0 since the left-hand limit at x=0 is equal to the right-hand limit at x =0 and both of the limits are equal to the value of the function at x=o. The function f(x) as shown in the second graph is not continuous at x =0 since the left-hand limit and right-hand limit are not equal to each other. Moreover, in the second graph, the value of the function at x <0 is f(x) =-1 while at x>0 value of the function abruptly changes [i.e f(x) =3] , In other words, a function that can be drawn without lifting the pen is always continuous and a function is drawn after lifting the pen because of a sudden change in its value.
Continuity and Differentiability
Table of content
- Definition of the continuity
- Definition of differentiability
- Example on Continuity and Differentiability
- Video on Continuity and Differentiability
You can also study
Definition of the Continuity
In mathematics, if a function f(x) exists then the function f(x) is said to be continuous at x=a if its left-hand limit, right-hand limit, and the value of the function are equal.
If a function doesn’t exist then it is called a discontinuous function
A function is said to be a continuous function in an open interval if it is continuous at every point within (a,b)
A function is said to be a continuous function in a closed interval [a,b] if it is continuous at every point within (a,b) and at the points, a and b or in short the RHL of f(x) at point a is equal to LHL of f(x) at a point b or more simply the limit of the function at a is equal to the limit of the function at b.
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
Definition of the differentiability
A function f(x) is said to be differentiable at the point x=a .If f ‘(x) exist then the value of f ‘(a) is determined as follows.
Here h is the infinitesimal value that is almost equal to 0 but not equal to 0.
Examples.
Consider the following function
Discussing its continuity and differentiability at x=1
∴ Given function is continuous at x = 1
Now determining the derivative of the function at x = 1
F(x) is not differentiable at x =1,therefore the given function is continuous but not differentiable at x =1
See the video
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT solutions for class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Class 12 Maths Important Questions-Application of Integrals
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution
NCERT Solutions for class 9 maths
NCERT Solutions for class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions