NCERT Solutions for Class 11 Maths Miscellaneous Exercise Chapter 1 Sets
NCERT Solutions for Class 11 Maths Miscellaneous Exercise Chapter 1 Sets are the most important for the preparation of class 11 maths for examination purposes because NCERT Solutions for Class 11 Maths Miscellaneous Exercise Chapter 1 Sets contains the solutions of all type of questions available in Miscellaneous Exercise Chapter 1 Sets .Miscellaneous Exercise Chapter 1 Sets of class 11 maths is the extract of all the exercises from 1.1 to 1.6 hence study of this exercise enable you to clear all the concepts on sets that is necessary for proper understanding of the questions when you would face your maths exam.
NCERT Solutions for Class 11 Maths Miscellaneous Exercise Chapter 1 Sets
Q1. Decide ,among the following sets, which sets are subsets of one and another:
A = {x : x ∈ R and x satify x²-8x + 12 =0}
B ={2,4,6}
C ={2,4,6,8}
D ={6}
Ans. A = {x : x ∈ R and x satify x²-8x + 12 =0}
Solving the equation
x²-8x + 12 =0
x² -6x -2x +12 =0
x(x -6) -2(x -6) = 0
( x-6)(x -2) =0
x =6,2
∴ A = {2,6}
B ={2,4,6},C ={2,4,6,8},D ={6}
It is clear that
A⊂ B,A⊂C, B ⊂ C, D ⊂A, D⊂B,D⊂C
Q2.In each of the following, determine whether the statement is true or false. If it is true, give an example.
(i) If x ∈A and A ∈B,then x∈ B
(ii)If A⊂ B and B ∈C then A∈C
(iii)If A⊂B and B⊂ C then A⊂C
(iv)If A ⊄ B and B ⊄ C then A ⊄C
(v) If x ∈A and A ⊄ B then x∈B
(vi) If A ⊂B and x∉B then x ∉ A
Ans.
(i) We are given that if x ∈A and A ∈B Then x∈ B
Let A = {1,2} and B={{1,2},3,4}
1∉ B or 2 ∉ B,so it is false
(ii) If A⊂ B and B ∈C then A∈C
Let A ={1,2},B={1,2,3},C={5,6,{1,2,3},7}
Here A⊂B and B ∈C but A ∉C,so it is false
(iii)If A⊂B and B⊂ C then A⊂C
Let A ={1,2} ,B ={1,2,,3} ,C ={1,2,,3,4}
Here A⊂C,so it is true
(iv)If A ⊄ B and B ⊄ C then A ⊄C
Let A={1,2},B={3,4},C={1,2,5,6}
Here A⊂C,so it is false
(v) If x ∈A and A ⊄ B then x∈B
Let A={1,2,3}, B={1,2,4,5}
Here 3 ∉B,so it is false
(vi) If A ⊂B and x∉B then x ∉ A
Let A={1,2,3}, B={1,2,3,4,5}
Here 6 ∉B 6 ∉A, so it is true
NCERT Solutions for Class 11 Maths Miscellaneous Exercise Chapter 1 Sets
Q3. Let A, B, and C be the sets such that A ∪ B = A ∪ C and A ∩ B = A ∩ C. show that B = C.
Ans. The given sets A, B, and C are such that A ∪ B = A ∪ C and A ∩ B = A ∩ C
In order to prove B=C, let’s prove B⊂C and C⊂B
Let x ∈B
x∈ A ∪ B (Every element belongs to B also the elements of A ∪ B)
x ∈A ∪ C(Since A ∪ B = A ∪ C)
⇒ x∈A or x ∈C
In the first case x ∈ A
Also x∈B
Therefore x∈A ∩ B ( x is common in the set A and set B)
Since A ∩ B = A ∩ C
∴ x∈A ∩ C
⇒x ∈A and x∈C
∴ If x ∈ B then x∈C
Therefore B⊂ C (Every element of B belongs to the set C)….(i)
Similarly we can solve C⊂B….(ii)
From (i) and (ii) equation
B = C,Hence proved
Click-For online purchasing of Computer and Accessories
Q4. Show that the following four conditions are equivalent:
(i) A ⊂ B (ii) A – B = Φ
(iii) A ∪ B = B (iv) A ∩ B = A
Ans. Showing the condition (i) A ⊂ B and (ii) A – B = Φ are equivalent or not
A ⊂ B shows that every elements of A is available in B
Therefore A – B = Φ
Hence both conditions are equivalent
Showing the condition (ii) A – B = Φ and A ∪ B = B are equivalent
A ∪ B = B shows that all the elements of A are in B
Therefore A -B=Φ
NCERT Solutions for Class 11 Maths Miscellaneous Exercise Chapter 1 Sets
Q5.Show that if A ⊂ B, then C – B ⊂ C – A.
Ans. The condition given to us is
A⊂B (all the elements of A are in the set B)
Let x ∈ C – B…..(i)
⇒x ∈ C and x∉B
Since A⊂B
∴ x∈C and x∉A
Therefore x∈ C -A….(ii)
From (i) and (ii)
C – B ⊂ C -A,Hence proved
Q6.Assume that P (A) = P (B). Show that A = B
Ans. We are given that
P (A) = P (B)
In order to prove A = B,let’s prove A⊂B and B⊂A
P(A) is the power set of the set A implies all subsets of A belongs to P(A)
A is one of the subset of A
∴ A ∈ P(A) [ e.g Let A ={1,2} then P(A) ={{1},{2},{1,2},Φ}⇒{1,2}∈P(A) ]
Since P (A) = P (B)
∴ A ∈ P (B)
If set A is in the power set of B then all the elements of set A is in set B
∴A⊂ B…..(i)
Similarly we can show B⊂A….(ii)
From (i) and (ii)
A = B
NCERT Solutions for Class 11 Maths Miscellaneous Exercise Chapter 1 Sets
Q7. Is it true that for any sets A and B, P (A) ∪ P (B) = P (A ∪ B)? Justify your answer.
Ans. For justifying P (A) ∪ P (B) = P (A ∪ B),let us take an examples
Let A = {1,2} and B ={2,3}
∴ A∪B ={1,2,3}….(i)
P(A) = {{1},{2},{1,2},Φ} and P(B) = {{2},{3},{2,3},Φ}
P (A) ∪ P (B) = {{1},{2},{1,2},{3},{2,3},Φ}….(ii)
From (i) equation
P (A ∪ B) = {{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3},Φ}…(iii)
From equation (ii) and the equation (iii),we have
P (A) ∪ P (B) ≠ P (A ∪ B)
Q8.Show that for any sets A and B,
A = (A ∩ B) ∪ (A – B) and A ∪ (B – A) = (A ∪ B)
Ans. For showing
A = (A ∩ B) ∪ (A – B)
Taking RHS
(A ∩ B) ∪ (A – B)
=(A ∩ B) ∪ (A∩ B’)[ Since A -B =(A∩ B’)]
Applying the distributive property of the sets (X ∩ Y) ∪ (X∩ Z)=X ∩ (Y∪Z)
= A∩(B∪B’)
= A∩U ( Since U =B∪B’)
= A =RHS
For showing A ∪ (B – A) = (A ∪ B)
Taking LHS
A ∪ (B – A)
=A∪(B∩A’) [ Since A -B =(A∩ B’)]
=(A∪B)∩ (A∪A’)[ Distributive property of the sets]
=(A∪B)∩U[Since A∪A’= U]
=A∪B= RHS,Hence proved
Q9. Using properties of sets, show that:
(i) A ∪ (A ∩ B) = A
(ii) A ∩ (A ∪ B) = A
Ans. (i) We have to show A ∪ (A ∩ B) = A
Taking LHS A ∪ (A ∩ B)
Applying distributive property
= (A∪A) ∩(A∪B)
= A ∩(A∪B) (since A∪A =A)
= A=RHS (since all elements of A are in A∪B)
(ii) We have to show A ∩ (A ∪ B) = A
Applying distributive property
= (A∩A)∪(A∩B)
= A ∪(A∩B)
= A=RHS [ from (i) ]
NCERT Solutions for Class 11 Maths Miscellaneous Exercise Chapter 1 Sets
Q10.Show that A ∩ B = A ∩ C need not imply B = C.
Ans.Let A = {1,2,3}, B = (2,3,4},C={2,3,5}
Here A ∩ B ={2,3} and A ∩ C ={2,3}
Hence A ∩ B = A ∩ C but B≠C
Q11.Let A and B be sets. If A ∩ X = B ∩ X = ϕ and A ∪ X = B ∪ X for some set X, show that A = B.
(Hints A = A ∩ (A ∪ X) , B = B ∩ (B ∪ X) and use Distributive law)
Ans.We are given three sets A,B and X such that
If A ∩ X = B ∩ X = ϕ and A ∪ X = B ∪ X
We have to prove
A = B
Taking LHS
A = A ∩ (A ∪ X) [ Using the property of the sets]
= (A∩A) ∪ (A∩X) (Using the distributive property of the sets]
=A∪(A∩X)
=A∪(B∩X) (it is given to us A∩X =B∩X)
=(A∪B)∩(A∪X)[Using the distributive property of the sets]
=(B∪A)∩(B∪X)[Since A∪B = B∪A and it is given A ∪ X = B ∪ X]
=B∩(A∪X)
=B∩(B∪X)[it is given that A∪X =B∪X]
=B( property of the sets B= B∩(B∪X)
Hence A = B
Q12.Find sets A, B and C such that A ∩ B, B ∩ C and A ∩ C are non-empty sets and A ∩ B ∩ C = Φ.
Ans.We are given A ∩ B, B ∩ C and A ∩ C are non-empty sets
Let A = {1,2}, B = (1,3},C = {2,3}
According to the question
A ∩ B = {1}
B ∩ C ={3}
A ∩ C ={2}
Here A ∩ B, B ∩ C and A ∩ C are non-empty sets
Therefore we get A ∩ B ∩ C = Φ
See the video for the solutions of the questions from 8 to 12
See the video for NCERT Solutions of the Chapter 1 Exercise 1.6
Q13.In a survey of 600 students in a school, 150 students were found to be taking tea and 225 taking coffee, 100 were taking both tea and coffee. Find how many students were taking neither tea nor coffee
Ans. The survey was taken of 600 students ,n(U) = 600
The number of students who took tea = n(T) = 150
The number of students who took coffee = n(C) = 225
The number of students who took both tea and coffee = n(T∩C) = 100
For getting students who were taking neither tea nor coffee,let’s determine the students who were taking either tea or coffee, i.e n(T∪C)
We have
n(T∪C) = n(T) + n(C) – n(T∩C)
n(T∪C)= 150 + 225 – 100 = 275
The number of persons who were taking neither tea nor coffee =n(U) –n(T∪C) = 600 -275 = 325
Q14. In a group of students, 100 students know Hindi, 50 know English and 25 know both. Each of the students knows either Hindi or English. How many students are there in the group?
Ans.The number of students who know Hindi,n(H) =100
The number of students who know English,n(E) =50
The number of students who know both Hindi and English n(H∩E) =25
The number of students in the group are n(H∪E) =?
We have
n(H∪E) = n(H) + n(E) – n(H∩E)
=100 +50 -25 =125
Hence the number of students in the group are 125
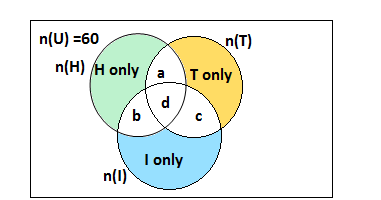
Q15.In a survey of 60 people, it was found that 25 people read newspaper H, 26 read newspaper T, 26 read the newspaper I, 9 read both H and I, 11 read both H and T, 8 read both T and I, 3 read all three newspapers. Find:
(i) The number of people who read at least one of the newspapers.
(ii) The number of people who read exactly one newspaper.
Ans. Total number of people surveyed are 60,so n(U) = 60
The number of the people who read news paper H,n(H) = 25
The number of the people who read news paper T,n(T) = 26
The number of the people who read news paper I,n(I) = 26
The number of the people who read both news paper H and I,n(H∩I) = 9
The number of the people who read both news paper H and T,n(H∩T) = 11
The number of the people who read both news paper T and I,n(T∩I) = 8
The number of the people who read all three news paper n(H∩T∩I) = 3
(i) We have to determine the number of people who read at least one of the newspapers,n(H∪T∪I) =?
n(H∪T∪I) = n(H) +n(T)+n(I)-n(H∩T)-n(T∩I) -n(H∩I)+n(H∩T∩I)
= 25 +26 +26 -11-8-9 + 3
= 80 -28 = 52
Hence the number of people who read at least one of the newspaper is 52
(ii) Now, we have to determine the number of people who read exactly one newspaper.
Drawing the venn diagram
It is shown in the venn diagram, we have to find out the colour portions
Here n(H∩T)=a+d=11, n(H∩I)=b+d=9 and n(T∩I)=d+c=8,d =n(H∩T∩I)=3
We are required to find out
n(H∩T) + n(H∩I)+ n(T∩I) =11+9+8 =28
a +d + b+d +d+c =28
But as it is seen in the venn diagram 28 is the sum of a,b,c and d
a +b+c+d =28 -2d
It is given to us,d =n(H∩T∩I)=3
a + b+c +d = 28 -2×3 =28 -6 =22
The number of people who read exactly one newspaper = 52 -22 = 30
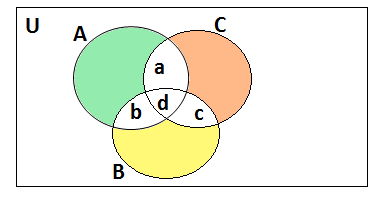
Q16. In a survey it was found that 21 people liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked products B and C and 8 liked all the three products. Find how many liked product C only.
Ans.The number of people who liked product A ,n(A) = 21
The number of people who liked product B ,n(B) = 26
The number of people who liked product C,n(C) = 29
The number of people who liked product A and B ,n(A∩B) = 14
The number of people who liked product B and C ,n(B∩C) = 14
The number of people who liked product C and A ,n(C∩A) = 12
The number of people who liked all three products A and B and C ,n(A∩B∩C) = 8
Drawing the venn diagram
n(A∩B) = 14⇒b +d = 14
d = n(A∩B∩C) = 8
b= 14 – 8 = 6
n(B∩C) = 14 ⇒d +c = 14
8 +c =14
c = 14 – 8 = 6
n(C∩A) = 12⇒a +d =12
a + 8 =12
a = 12 -8 = 4
The people who liked product C only = n(C) – (a +d +c) =29 -(4 +8+6) =29-18=11
You can compensate us by donating any amount of money for our survival
Our Paytm NO 9891436286
You can also study
NCERT Solutions for Class 11 Chapter 1 Sets
Chapter 1 Sets -Important questions
Download PDF NCERT Solutions of the Chapter 1-Sets
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions of class 9 maths
| Chapter 1- Number System | Chapter 9-Areas of parallelogram and triangles |
| Chapter 2-Polynomial | Chapter 10-Circles |
| Chapter 3- Coordinate Geometry | Chapter 11-Construction |
| Chapter 4- Linear equations in two variables | Chapter 12-Heron’s Formula |
| Chapter 5- Introduction to Euclid’s Geometry | Chapter 13-Surface Areas and Volumes |
| Chapter 6-Lines and Angles | Chapter 14-Statistics |
| Chapter 7-Triangles | Chapter 15-Probability |
| Chapter 8- Quadrilateral |
NCERT Solutions of class 9 science
CBSE Class 9-Question paper of science 2020 with solutions
CBSE Class 9-Sample paper of science
CBSE Class 9-Unsolved question paper of science 2019
NCERT Solutions of class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT solutions of class 10 science
Solutions of class 10 last years Science question papers
CBSE Class 10 – Question paper of science 2020 with solutions
CBSE class 10 -Latest sample paper of science
NCERT solutions of class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions of class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |