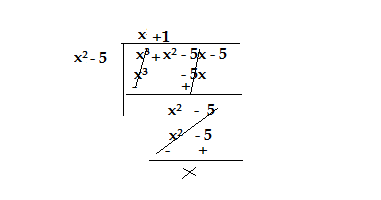Skip to content 
Class 10 maths MCQ Chapter 2 Polynomial with detail Solutions for Term-1 CBSE Board Exam
Class 10 maths MCQ Chapter 2 Polynomial with detail Solutions for Term-1 CBSE Board Exam 2021 are created here by an expert of maths for helping the students in their preparation of Term-1 CBSE Board Exam 2021.Study of these Class 10 maths MCQ Chapter 2 Polynomial with detail Solutions for Term-1 CBSE Board Exam will give you an idea about the type of the questions in Term-1 CBSE Board exam 2021,therefore for achieving excellent percentage in maths every student is required to study MCQ’s of every chapters. Since pattern of question paper is changed so after studying the chapters of NCERT you are required study of these MCQ’s which are addiional questions prepared for Term 1 CBSE board exam 2021.
Class 10 maths MCQ Chapter 2 Polynomial with detail Solutions for Term-1 CBSE Board Exam
olutions of class 10 last years Science and maths question papers
Class 10 Maths MCQ with solutions-Trigonometry for Term-1
Class 10 science sample paper for term-1 2021 with Solutions
Class 10 maths sample paper for term-1 2021 with Solutions
CBSE Class 10 – Question paper of science 2020 with solutions
CBSE class 10 -Latest sample paper of science
Class 10 maths MCQ Chapter 2 Polynomial with detail Solutions for Term-1 CBSE Board Exam
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
Q1.If one zero of the polynomial x² +3x +k is 2,then the value of k is
(a) 10 (b)-10 (c) 5 (d) -5
Ans. (b) -10
If x is the zero of the polynomial then P(x) =0
∴ P(2) = 2² +3×2 +k
0 =4 +6 +k
10 +k =0
k =-10
Q2.Given that two of the zeroes of the cubic polynomial ax³ +bx² + cx +d are 0,the third zero is
(a) -b/a (b) b/a (c) c/a (d) -d/a
Ans.If two of the zeroes are 0(α,β ), then applying the relationship between zeroes and coefficients of the polynomial,ax³ +bx² + cx +d
α+β+γ = -b/a (where α,β,γ are the zeroes of the polynomial)
0+0+γ =-b/a
γ = -b/a
Therefore, third zero is -b/a
Q3. If one of the zeroes of the quadratic polynomial (k – 1) x² + kx + 1 is – 3, then the value of k is
(a) 4/3 (b) -4/3 (c) 2/3 (d) -2/3
Ans. (a) 4/3
The given polynomial is (k – 1) x² + kx + 1 is – 3
One of the zero of the given polynomial is -3
So,the given polynomial P(-3) = 0
(k – 1) (-3)² + k(-3) + 1 =0
9k -9 -3k +1 =0
6k =8
k = 8/6 = 4/3
Q4. A quadratic polynomial, whose zeroes are -3 and 4, is
(a) x² -x +12 (b) x² +x +12 (c) x²/2 -x/2 -6 (d) 2x² +2x -24
Ans.(c) x²/2 -x/2 -6
The given zeroes of the quadratic polynomial are -3 and 4
The quadratic polynomial with zeroes α and β is given as
x² – (α + β )x + αβ
Therefore putting the value of α =-3 and β =4
x² – (-3 + 4 )x + (-3)×4
x² – x -12
By multiplying a number to the polynomial doesn’t change the polynomial,so dividing it by 2
(1/2)(x² – x -12) = x²/2 – x/2 -6
Q5.If the zeroes of the quadratic polynomial x² + (a + 1) x + b are 2 and -3, then
(a) a =-1,b=-1 (b) a= 5,b = -1 (c) a = 2, b=-6 (d) a =0, b=-6
Ans.(d) a = 0,b =-6
The given quadratic polynomial is x² + (a + 1) x + b
Since the zeroes of the polynomial given to us are 2 and -3,theefore value of the polynomial should be zero at x =2 and x =-3
2² + (a +1)2 +b =0
4 + 2a + 2 +b =0
2a + b =-6……(i)
(-3)² + (a +1)(-3) + b =0
9 -3a -3 +b =0
-3a + b = -6…..(ii)
Substracting equation (ii) from equation (i)
5a = 0⇒ a = 0
Putting the value of a in equation (i)
b = -6
Shortcut Mathod
α + β = -B/A and αβ = C/A
2 -3 =-(a +1)/1 and 2×-3 =b/1
a +1 =1⇒ a =0 and b = -6
Q6.The number of polynomials having zeroes as -2 and 5 is
(a) 1 (b) 2 (c) 3 (d) more than 3
Ans. (d) more than 3
We can creat infinite polynomials by multiplying a polynomial by different numbers but their zeroes remains the same
Q7.Given that one of the zeroes of the cubic polynomial ax3 + bx² + cx + d is zero, the product of the other two zeroes is
(a) -c/a (b) c/a (c) 0 (d) -b/a
Ans.(a) -c/a
Applying the relationship between the sum of product of two zeroes and coefficient
αβ + βγ +γα = -c/a
Putting α = 0
βγ = -c/a
Q8.If one of the zeroes of the cubic polynomial x3 + ax² + bx + c is -1, then the product of the
other two zeroes is
(a) b – a + 1
(b) b – a – 1
(c) a – b + 1
(d) a – b – 1
Ans. (a) b -a + 1
Applying the relationship between product of three zeroes and the coefficients of the polynomial
αβγ = -D/A = -c/1 = -c
Putting α = -1
-βγ = -c
βγ = c. but c is not there ,therefore getting the value of c by putting x =-1 since P(-1) =0
(-1)³ + a(-1)² +b(-1) +c = 0
-1 +a -b +c =0
c = b-a +1
βγ = b-a +1
Q9.The zeroes of the quadratic polynomial x² + 99x +127.
(a) both positive (b) both negative (c) one positive and one negative (d) both equal
Ans.(b) both negative
In the polynomial ax² +bx + c, if a >0,b>0 and c>0 or a <0,b <0 and c<0 then both roots are negative
In the given polynomial x² +99x +127, 1>0,99>0 and 127 >0,therefore given polynomial has both negative roots
Q10.If zeroes of a quadratic polynomial are -1/2 and 3,then the polynomial is
(a) x² -5x -3 (b) 2x² -10x + 3 (c) x² -10x + 5 (d) 4x² -10x – 6
Ans.(d) 4x² -10x – 6
The quadratic polynomial with zeros α and β is given as
x² – (α +β)x + αβ
Putting the value α =-1/2 and β = 3
x² – (-1/2 +3)x + (-1/2)3
x² – (-1 +6)x/2 -3/2
x² – (5/2)x -3/2
Multiplying it by 4
4x² -10 x -6
Q11. If the zeroes of the quadratic polynomial ax² + bx + c, c # 0 are equal, then
(a) c and a have opposite sign (b) c and b have opposite sign (c) c and a have the same sign (d) c and b have the same sign
Ans.c and a have the same sign
If two zeros are equal then the polynomial should be a complete square ,as an example (x -2)² or (x +2)²
The expansions of them are x² – 2x + 4 or x² + 2x + 4, here a =1 and c =4 in both equation,therefore the accurate answer is both a and c should have same sign when both roots are equal
Q12.The polynomial whose zeros are the reciprocal of the zeros of quadratic polynomial ax² +bx +c is
(a) x² +x +1 (b) x² +bx -a (c) cx² +bx + a (d) x² -cx + a
Ans.(c) cx² +bx + a
Let the zeros of the given polynomial ax² +bx +c are α and β
We know
α + β = -b/a and α β = c/a
According to question the zeros of the required polynomial are 1/α and 1/β
Therefore the polynomial is given as
x² – (1/α + 1/β)x + αβ
x² – (α + β)x/ αβ + 1/αβ
cx² +bx + a
Q12.If α and β are the zeros of the polynomial f(x) = x² +x + 1,then 1/α + 1/β = ?
(a) 1 (b) -1 (c) 0 (d) None of these
Ans.(b) -1
The given zeros of the the polynomial f(x ) =x² +x + 1 are α and β
Therefore
α + β = -b/a = -1/1 = -1….(i) ,αβ = c/a = 1/1 =1…..(ii)
1/α + 1/β =( α + β)x/ αβ
Putting the value of (α + β) and αβ from equation (i) and equation (ii)
Q13.If zero of the polynomial f(x) = (k² +4)x² +13x +4k is reciprocal of the other,then k=
(a) 2 (b) -2 (c) 1 (d) -1
Ans.(a) 2
Let one zero of the given polynomial f(x) = (k² +4)x² +13x +4k is α then other is 1/α
We know the relationship between the coefficients and the zeros of the polynomial ax² +bx +c
αβ = -b/a
Putting β =1/α and a = (k² +4) and c = 4k
α . 1/α = 4k/(k² +4)
4k/(k² +4) = 1
k² +4 = 4k
k² -4k +4 =0
(k -2)² = 0
k – 2 = 0⇒ k = 2
Q14. If the sum of the zeros of the polynomial f(x) =2x³ -3kx² +4x -5 is 6,then value of k is
(a) 2 (b) 4 (c) -2 (d) -4
Ans.(b) 4
Given zero of the given polynomial f(x) =2x³ -3kx² +4x -5 is 6
The relationship between the coefficients and the zeros of the polynomial ax³ +bx² +cx +d is given as
α+β+γ = -b/a
6 = -(-3k)/2
3k = 12 ⇒k = 4
Q15.If α,β are the zeros of polynomial f(x) =x² -p(x +1) -c,then (α +1)(β +1) =
(a) c -1 (b) 1 -c (c) c (d) 1 +c
Ans.(b) 1 -c
We have to find o
From the polynomial f(xut the value of (α +1)(β +1)
Expanding the given expression
(α +1)(β +1)
=αβ + α + β + 1) =x² -p(x +1) -c=x² -px -p -c=x²-px -(p +c) wehere a =1,b =-p,c = -(p+c),we have
α + β = -b/a = p/1 =p and αβ = c/a = -(p+c)/1 =-(p+c)
∴(α +1)(β +1) = -(p+c) + p +1 = -p-c +p+1 = 1-c
Q16.If the product of zeros of the polynomial f(x) = ax³ -6x² +11x -6 is 4,then a =
(a) 3/2 (b) -3/2 (c) 2/3 (d) -2/3
Ans.(a) 3/2
Let the zeros of the given polynomial are α,β and γ
From the given polynomial f(x) = ax³ -6x² +11x -6,we have a =a,b =-6,c = 11 and d = -6
The relationship between the coefficients and the zeros is
αβγ = -d/a = -(-6)/a=6/a
Since αβγ = 4 is given to us
6/a = 4
4a = 6⇒a =6/4 = 3/2
Q17.If α,β,γ are the zeros of the polynomial f(x) =ax³ +bx² +cx +d,then α²+β² +γ² =
(a) (b²-ac)/a² (b) (b²-2ac)/a (c) (b²+2ac)/b² (d) (b²-2ac)/a²
Ans. (d) (b²-2ac)/a²
From the given polynomial f(x) =ax³ +bx² +cx +d,we have, B =b and A =a , C=c,α,β,γ are the zeros
α+β+γ = -B/A =-b/a and αβ +βγ +γα = c/a
Squaring both sides,we have
(α+β+γ)² = (-b/a)²
α²+β²+γ²+2αβ +2βγ +2γα = b²/a²
α²+β²+γ² + 2(αβ +βγ +γα) = b²/a²
α²+β²+γ² + 2c/a = b²/a²
α²+β²+γ² = b²/a² -2c/a = (b²-2ac)/a²
Q18. If α,β,γ are the zeros of the polynomial f(x) =x³ -px² +qx -r,then 1/αβ+1/βγ +1/γα =
(a) r/p (b) p/r (c) -p/r (d) -r/p
Ans.(b) p/r
From the given polynomial f(x) =x³ -px² +qx -r,we have, b =-p and a =1 , c=q,d =-r
α+β+γ = -b/a =-(-p)/1 =p and αβγ = -d/a=-(-r)/1 = r
We have to find out 1/αβ+1/βγ +1/γα =
Simplifying the given expression
1/αβ+1/βγ +1/γα = (α +β +γ)/αβγ
Substituting the values of (α +β +γ) and αβγ
1/αβ+1/βγ +1/γα = p/r
Q19.If the polynomial f(x) =ax³ +bx -c is divisible by the polynomial g(x) =x² +bx +c,then ab is
(a) 1 (b) 1/c (c) -1 (d) -1/c
Ans.(a) 1
Dividing the given polynomial ax³ +bx -c by another given polynomial x² +bx +c
Since f(x) is divisible by g(x),the remainder should be 0
(b – ac -ab²)x + abc -c =0
b – ac -ab² = 0 and abc -c =0⇒abc = c⇒ab =1
Q20.What should be added to the polynomial x² -5x +4, so that 3 is the zero of the resulting polynomial ?
(a) 1 (b) 2 (c) 4 (d) 5
Ans.(b) 2
The given polynomial is x² -5x +4
Since 3 is the zero of the resulting polynomial therefore (x -3) should be one of the factor of the resulting polynomial
Therefore dividing the given polynomial by x -3,we can get the remainder
3² -5×3 +4 = 9 -15 +4 =-2
Hence -(-2) = 2 should be added to the given polynomial so that the resulting polynomial has 3 as a one of the zeros.
Q21. If α,β are the zeros of the polynomial f(x) = ax² +bx +c,then 1/α² + 1/β² =
(a) (b² -2ac)/a² (b) (b² -2ac)/c² (c) (b² +2ac)/a² (d) (b² +2ac)/c²
Ans.(b) (b² -2ac)/c²
From the given polynomial f(x) = ax² +bx +c,we have a =a,b =b,c =c and zeros given are α and β
The relationship between the coefficients and zeros are
α + β = -b/a and α β = c/a
⇒(α + β )²= (-b/a)² and α² β²=c²/a²
α² +β² +2αβ = b²/a² and α² β²=c²/a²
α² +β² = b²/a² – 2αβ and α² β²=c²/a²
α² +β² = b²/a² -2×c/a and α² β²=c²/a²
α² +β² =(b² -2ac)/a²….(i) and α² β²=c²/a²
Simplifying the given expression
1/α² + 1/β² = (α² +β²)/α²β²
From equation (i) and equation (ii)
Q22. If two zeros of x³ -x² -5x -5 are √5 and -√5 then third zero is
(a) 1 (b) -1 (c) 2 (d) -2
Ans.(b) -1
If √5 and -√5 are the zeros of the polynomial x³ + x² -5x -5,then its two factors must be (x -√5) and (x +√5) and
their product (x -√5) (x +√5)=x² -5 also should be the factor of the given polynomial
Therefore dividing the given polynomial by (x² -5)
Therefore it will have more factor (x +1)
Hence the x+1=0⇒x =-1
Q23. If x + 2 is a factor of x² +ax +2b and a + b =4 then
(a) a =1,b =3 (b) a =3,b=1 (c) a = -1, b = 5 (d) a =5,b = -1
Ans.(b) a =3,b=1
If (x +2) is the factor of x² +ax +2b then x = -2 will be its one of the zero
Therefore at x =-2 the value of polynomial is equal to zero
(-2)² + a(-2) + 2b =0
4 -2a + 2b =0
-2a + 2b = -4
-a + b = -2…..(i)
The given equation is a + b = 4….(ii)
Adding both equation
2b = 2⇒ b = 1
Putting the value of b in equation (ii)
a +1 =4
a = 4-1 =3
Q24.The polynomial which when divided by -x² + x -1 gives a quotient x -2 and remainder 3, is
(a) x³ -3x² +3x -5 (b) -x³ +3x² -3x -5 (c) -x³ +3x² -3x +5 (d) -x³ -3x² -3x +5
Ans.(c) -x³ +3x² -3x +5
If a polynomial p(x) is divided by g(x) gives quotient q(x) and remainder r(x) then
p(x) = g(x) q(x) + r(x)
Here g(x) =-x² + x -1, q(x) = x -2 and r(x) =3
Therefore
p(x) =( -x² + x -1)(x -2) + 3 = -x³ +2x² +x² -2x -x + 2 +3 =-x³ +3x² -3x + 5
You can compensate us by donating any amount of money for our survival
Our Paytm No 9891436286
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions of class 9 maths
| Chapter 1- Number System | Chapter 9-Areas of parallelogram and triangles |
| Chapter 2-Polynomial | Chapter 10-Circles |
| Chapter 3- Coordinate Geometry | Chapter 11-Construction |
| Chapter 4- Linear equations in two variables | Chapter 12-Heron’s Formula |
| Chapter 5- Introduction to Euclid’s Geometry | Chapter 13-Surface Areas and Volumes |
| Chapter 6-Lines and Angles | Chapter 14-Statistics |
| Chapter 7-Triangles | Chapter 15-Probability |
| Chapter 8- Quadrilateral |
NCERT Solutions of class 9 science
CBSE Class 9-Question paper of science 2020 with solutions
CBSE Class 9-Sample paper of science
CBSE Class 9-Unsolved question paper of science 2019
NCERT Solutions of class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT solutions of class 10 science
Solutions of class 10 last years Science question papers
CBSE Class 10 – Question paper of science 2020 with solutions
CBSE class 10 -Latest sample paper of science
NCERT solutions of class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions of class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
