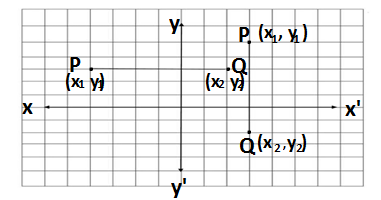Skip to content 
NCERT Solutions for Class 11 Maths Exercise 10.1 Chapter 10 Straight Lines
NCERT Solutions for Class 11 Maths Exercise 10.1 Chapter 10 Straight Lines are created here for helping the class 11 maths students for the preparation of maths subjects in the CBSE board exam. NCERT Solutions for Class 11 Maths Exercise 10.1 Chapter 10 Straight Lines will help you in clearing your maths concept on coordinate geometry of straight lines which is required to solve other exercises of chapter 10 straight lines.NCERT Solutions for Class 11 Maths Exercise 10.1 Chapter 10 Straight Lines are solved by a step by step method so every student can understand the solutions .
NCERT Solutions for Class 11 Maths
NCERT solutions of class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
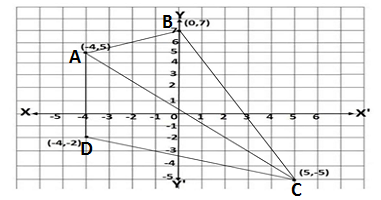
Q1. Draw a quadrilateral in a cartesian plane,whose vertices are (-4,5),(0,7),(5,-5) and (-4,-2). Also, find its area.
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
Ans.
ar ABCD = ar ΔABC +arΔADC
The area of the triangle whose vertices are (x1,y1),(x2,y2) and (x3,y3)
1/2[x1(y2-y3) +x2(y3-y4)+x3(y2-y3)]
ar ΔABC = -29
Area can’t be – so area of ΔABC = 29 units
arΔ ADC = 1/2(75 -12) =63/2 = 31.5
Therefore area of ABCD = 29 +31.5 = 60.5 sq.unit
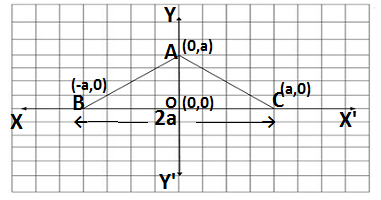
Q2.The base of an equilateral triangle with side 2a lies along the y-axis such that the midpoint of the base is at the origin . Find vertices of the triangle.
Ans.
Let the vertices of the triangle are A,B and C where BC is the base of the triangle
AB =BC = AC (Since ΔABC is an equilateral triangle)
BC = 2a (Given)
The midpoint of AC is origin O, therefore coordinates of O are (0,0)
As seen in the diagram OB = OC = a
Therefore vertices of B are (-a,0) and of C are (a,0)
In ΔABC , AC = 2a
AO ⊥BC, so OA = √(AC²- OC²) =√[(2a)²- a²] = √(4a²-a²) = a√3
Therefore vertices of A are (a√3,0) since the vertex of A is on Y-axis so it may be on the negative Y-axis, therefore coordinates of A are (±a√3,0)
Q3.Find the distance between P(x1,y1) and Q(x2,y2) when (i) PQ is parallel to the Y-axis (ii) PQ is parallel to the x-axis.
Ans. The points P and Q are given in both cases when PQ is parallel to X-axis and PQ is parallel to Y-axis.
The distance between P and Q when PQ is parallel to X axis
Here y1=y2
The distance between P and Q when PQ is parallel to X axis
Here x1=x2
Q5. Find the slope of a line, which passes through the origin, and the mid-point of the line segment joining the points P (0, – 4) and B (8, 0).
Ans. The mid point of the line segment joining the points P (0, – 4) and B (8, 0) = (0 +8)/2, (-4 +0)/2 = (4,-2)
It is given that the line is passing through the origin (0,0) and (4,-2)
The slope(m) of the line segment joining the points P(x1,y1) and Q(x2,y2)
is given as follows
Therefore the required slope of the line is -1/2
See the video for the solutions of Q1 to Q5 of Exercise 10.1 Straight Lines
Q6.Without using the Pythagoras theorem, show that the points (4,4),(3,5), and (-1,-1) are the vertices of a right-angled triangle.
Ans.The given vertices of the triangle are (4,4),(3,5), and (-1,-1)
Let the triangle is ΔABC, where A(4,4),B(3,5) and C(-1,-1)
The slope of the line joining the points (x1,y1) and (x2,y2) = (y2-y1)/ (x2-x1)
The slope of AB
The slope of BC
The slope of AC
The condition of the two lines whose slopes are m1and m2
m1 m2=-1
The slope of AC ×The slope of AB =1×-1 = -1
Therefore AC ⊥AB and BC is the hypotenuse of the right triangle
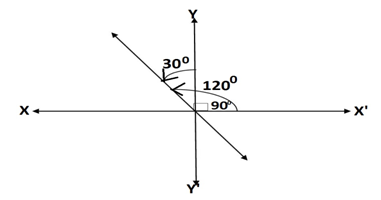
Q7.Find the slope of the line, which makes an angle of 30° with the positive direction of y-axis measured anticlockwise.
Ans. The line described in the question is as shown below
The line makes an angle of 30° with the positive direction of y-axis anticlockwise also makes an angle (90° +30°=120°) with the positive direction of x-axis anticlockwise
Hence the slope of the line is = tan120°
m= tan(π -60°)
m = -tan 60°= -√3
Therefore slope of the given line is -√3
Q8.Find the value of x for which the points (x, – 1), (2, 1) and (4, 5) are collinear.
Ans.Three points A(x1,y1) , B(x2,y2) and C(x3,y3) are collinear when the slope of the line segment AB = Slope of the line segment BC
Here the points given to us are A(x, – 1), B(2, 1), and (4, 5)
4- 2x = 2
2x = 2⇒ x = 1
∴ The required value of x is 1
Q9.Without using the distance formula, show that points (– 2, – 1), (4, 0), (3, 3), and (–3, 2) are the vertices of a parallelogram.
Ans. Let the points given to us are named as A(– 2, – 1), B (4, 0), C (3, 3) and D(–3, 2)
In a parallelogram opposite sides are parallel
Therefore slope of two pairs of line segments among AB,BC,DC and AD must be equal to each other
Slope of AB
Slope of BC
Slope of DC
Slope of AD
Since slope of AB = Slope of DC
∴AB ∥ DC
Since slope of AD = Slope of BC
∴AD ∥ BC
Hence ABCD is a parallelogram
See the video for the solutions of the Q6 -Q9
Q10. Find the angle between the x-axis and the line joining the points (3, -1) and (4, -2).
Ans. Let he x axis makes an angle θ with the line joining two points (3,-1) and (4,-2)
For this let’s find the slope of the joining the given points i.e m = tan θ
The slope of m = (-2 +1)/(4 -3) = -1/1 = -1
tan θ = -1
tan θ = -tan 45°
tan θ = tan (180° -45°) [ Since tan θ is negative,so it lies on second quadrant]
tan θ = tan 135°
θ = 135°
Therefore the angle between the x axis and the given line is 135°
Q11.The slope of a line is double of the slope of another line. If tangent of the angle between them is 1/3, find the slopes of the lines.
Ans. Let the slope of a line is m then slope of another line is 2m
We are given the tangent of the angle(θ )between them ,tan θ = 1/3
The angle between the two lines with slope m1 and m2is given as
Taking positve sign
1/3 = (-m/(1 +2m²)
1 + 2m² =-3m
2m² +3m +1 =0
2m² + 2m +m +1=0
2m(m +1) +1(m+1) =0
(m +1) (2m +1) =0
m =-1, m =-1/2
If slope of one line is -1 then slope of another line is -2 and if slope of one line is -1/2 then slope of another line is -1
Taking negative sign
1/3 = -(-m/(1 +2m²)
1 + 2m² =3m
2m² -3m +1 =0
2m² – 2m -m +1=0
2m(m -1) -1(m-1) =0
(m -1) (2m -1) =0
m =1, m =1/2
If slope of one line is 1 then slope of another line is 2 and if slope of one line is 1/2 then slope of another line is 1
Q12.A line passes through (x1, y1) and (h, k). If slope of the line is m, show that k -y1 = m (h -x1 ).
Ans. The equation of the line with the slope m that passes through the point (x1,y1) is given as
y -y1 = m (x -x1 )
The line is passing through (x1, y1) and (h, k)
m = (k-y1)/( h-x1)
k-y1= m ( h-x1), Hence proved
Q13. If three points (h, 0), (a, b) and (0, k) lie on a line, show that a/h + b/k = 1
Ans.Let the given point are A(h,0), B(a,b) and C(0,k) lie on a line
For the points A(h,0), B(a,b) and C(0,k) to be collinear
Slope of AB = Slope of AC
The slope of AB = (b-0)/(a -h) = b/(a-h)
Slope AC = (k-0)/(0-h) = k/-h
b/(a-h) =-k/h
-k( a-h) =bh
-ka +kh = bh
-ka -bh = -kh
ka + bh = kh
Dividing it by kh
ka/kh +bh/kh = 1
a/h + b/k = 1
Q14.Consider the following population and year graph (Fig 10.10), find the slope of the line AB and using it, find what will be the population in the year 2010?
Ans. Slope of the line AB = (97-92)/(1995-1985) = 5/10 = 1/2
Let the population in the year 2010 is a,in the graph it is represented by the point C along the line AB
So, the coordinates of the point C are (2010,a)
The slope of AB = Slope of BC
1/2 = (a-97)/(2010-1995)
1/2 = (a -97)/15
15/2 = a -97
7.5 = a -97
a = 97 + 7.5 = 104.5
Hence the slope of the line is 1/2 and the population in 2010 is 104.5
You can compensate us by donating any amount of money for our survival
Our Paytm NO 9891436286
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions of class 9 maths
| Chapter 1- Number System | Chapter 9-Areas of parallelogram and triangles |
| Chapter 2-Polynomial | Chapter 10-Circles |
| Chapter 3- Coordinate Geometry | Chapter 11-Construction |
| Chapter 4- Linear equations in two variables | Chapter 12-Heron’s Formula |
| Chapter 5- Introduction to Euclid’s Geometry | Chapter 13-Surface Areas and Volumes |
| Chapter 6-Lines and Angles | Chapter 14-Statistics |
| Chapter 7-Triangles | Chapter 15-Probability |
| Chapter 8- Quadrilateral |
NCERT Solutions of class 9 science
CBSE Class 9-Question paper of science 2020 with solutions
CBSE Class 9-Sample paper of science
CBSE Class 9-Unsolved question paper of science 2019
NCERT Solutions of class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT solutions of class 10 science
Solutions of class 10 last years Science question papers
CBSE Class 10 – Question paper of science 2020 with solutions
CBSE class 10 -Latest sample paper of science
NCERT solutions of class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions of class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
