Solutions of CBSE Board Class 12 Maths Exam Term 1 2021-22

Solutions of CBSE Board Class 12 Maths Exam Term 1 2021-22 are presented here to help class 12 CBSE students in re-examining the CBSE Board Class 12 Maths Exam Term 1 2021-22 by checking the answers and clearing doubts. The Solutions CBSE Board Class 12 Maths Exam Term 1 2021-22 will boost your confidence for future CBSE Board exams. Solutions of CBSE Board Class 12 Maths Exam Term 1 2021-22 is also helpful in boosting your preparation of the CBSE Board exam term 2 2021-22 . The solutions of CBSE Board Class 12 Maths Exam Term 1 2021-22 are created by an expert of mathematics as per the norms of CBSE by a simplified way for better understanding of mathematical concepts.

Q1. Differential of log [log(log x⁵)] w.r.t.x is

(a) 5/x log(x⁵) log(log x⁵) (b) 5/x log(log x⁵) (a) 5x⁴ / log(x⁵) log(log x⁵) (d) 5x⁴ / log(x⁵) log(log x⁵)

Ans. (d) 5x⁴ / log(x⁵) log(log x⁵)

Let y = log [log(log x⁵)]

$\frac{dy}{dx}=\frac{d}{dx}log\left [ log\left ( logx^{5} \right ) \right ]$

$=\frac{1}{log\left ( logx^{5} \right )}.\frac{d}{dx}log\left ( logx^{5} \right )$

$=\frac{1}{log\left ( logx^{5} \right )}.\frac{1}{logx^{5}}.\frac{d}{dx}x^{5}$

$=\frac{5x^{4}}{log\left ( x^{5} \right )log\left ( logx^{5} \right )}$

Click for online shopping

Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc

Q2. The number of all possible matrices of order 2 × 3 with each entry 1 or 2 is

(a) 16 (b) 6 (c) 64 (d) 24

Ans. The total number of possible matrices of order 2 × 3 with entry 1 or 0 is 64

Total elements = 2 × 3 =6

As total elements are 6 and each entry can be done is 2 ways. Hence, total possibilities = 2⁶= 64

Q3. A function f : R → R is defined as f(x) = x³ + 1. Then the function has

(a) no minimum value

(b) no maximum value

(c) both maximum and minimum values

(d) neither maximum value nor minimum value

Ans.(d) neither maximum value nor minimum value

The given function,f is defined as

f : R → R is defined as f(x) = x³ + 1

Let f(x) = y

y = x³ + 1

dy/dx = 3x²

For getting the terminal points(maximum point or minimum point)

dy/dx > for maximum point 0 or dy/dx <0 for minimum point

3x²> 0 or 3x²< 0 where it is given that x∈R

The value of f'(x) is limitless if we put x =1,2,3…(for maxima) and -1,-2,-3….(for minima)

Therefore f(x) has neither maximum value nor minimum value

Q4. If sin y = x cos (a + y), then dx/dy is

(a) cosa/cos² (a + y)

(b) – cos a/cos² (a + y)

(c) cos a/sin²y

(d) – cos a/sin²y

Ans.(a) cosa/cos² (a + y)

The given function is

sin y = x cos (a + y)

Solving it for x

x = sin y/cos (a + y)

$\frac{dx}{dy}=\frac{d}{dy}\left ( \frac{sin\: y}{cos\left ( a+y \right )} \right )$

$\frac{dx}{dy}=\frac{cos\left ( a+y \right )d/dy\left ( siny \right )-siny.d/dycos\left ( a+y \right )}{cos^{2}\left ( a+y \right )}$

$=\frac{cos\left ( a+y \right ).cosy-siny.\left [ -sin\left ( a+y \right ) \right ]}{cos^{2}\left ( a+y \right )}$

$=\frac{\left ( cosa.cosy-sina.siny \right )cosy+\left ( sina.cosy+cosa.siny \right )siny}{cos^{2}\left ( a+y \right )}$

$=\frac{cosa.cos^{2}y-sina.siny.cosy+sina.cosy.siny+cosa.sin^{2}y}{cos^{2}\left ( a+y \right )}$

$=\frac{cosa\left ( cos^{2} y+sin^{2}y\right )}{cos^{2}\left ( a+y \right )}$

$=\frac{cosa}{cos^{2}\left ( a+y \right )}$

Q5. The points on the curve x²/9 + y²/25 = 1, where the tangent is parallel to the x-axis are

(a) (± 5, 0) (b) (0, ± 5) (c) (0, ±3) (±3, 0)

Ans.(b) (0, ± 5)

The equation of x -axis is

y = 0

dy/dx = 0

The given equation of the curve is

x²/9 + y²/25 = 1

Differentiating the equation

(1/9) 2x + (1/25) 2y.dy/dx =0

(1/25) 2y.dy/dx =- (1/9) 2x

dy/dx = – (25/9) 2x/2y= -25x/9y

Since tangent is parallel to x -axis

∴Slope of the tangent = Slope of the x-axis

-25x/9y = 0

x = 0

Putting x =0 in equation of the curve

0/9 + y²/25 = 1

y²/25 = 1⇒ y = ±5

Hence the points on the curve where tangent is parallel to the x-axis are (0, ±5)

Q6.Three points P(2x, x +3), Q(0,x) and R(x +3, x +6) are collinear ,then x is equal to

(a) 0 (b) 2 (c) 3 (d) 1

Ans. (d) 1

It is given to us P(2x, x +3), Q(0,x) and R(x +3, x +6) are collinear

If three points are collinear then area of ΔPQR must be zero

Area of triangle =1/2[x₁(y₂-y₃) +x₂(y₃-y₁) + x₃(y₁-y₂) ]

1/2[x₁(y₂-y₃) +x₂(y₃-y₁) + x₃(y₁-y₂) ]=0

x₁(y₂-y₃) +x₂(y₃-y₁) + x₃(y₁-y₂) =0

x₁=2x, y₁=x +3, x₂=0,y₂=x and x₃=x +3, y₃=x +6

2x(x-x-6) +0(x+6-x-3) + (x+3)(x+3-x) =0

-12x +3x +9 =0

-9x +9 =0

x =1

Click for online shopping

Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc

Q7. The principal value of cos^-1(1/2) + sin^-1(-1/2) is

(a) π/12 (b) π (c) π/3 (d) π/6

Ans.(d) π/6

The given function is

cos^-1(1/2) + sin^-1(-1/2)

cos^-1(cos π/3) + sin^-1(-sin π/6)

cos^-1(cos π/3) -sin^-1(sin π/6) [since the range of cos θ is [0,π] and of sin θ is [-π/2,π/2]

Therefore principal value of the given function

π/3 -π/6 = (2π -π)/6 =π/6 =π/6

Q8.If (x² +y²)² = xy, then dy/dx is

$\left ( a \right )\frac{y+4x\left ( x^{2}+y^{2} \right )}{4y\left ( x^{2}+y^{2} \right )-x}$

$\left ( b \right )\frac{y-4x\left ( x^{2}+y^{2} \right )}{x+4\left ( x^{2}+y^{2} \right )}$

$\left ( c \right )\frac{y-4x\left ( x^{2}+y^{2} \right )}{4y\left ( x^{2}+y^{2} \right )-x}$

$\left ( d \right )\frac{4y\left ( x^{2}+y^{2} \right )-x}{y-4x\left ( x^{2}+y^{2} \right )}$

Ans.

$\left ( c \right )\frac{y-4x\left ( x^{2}+y^{2} \right )}{4y\left ( x^{2}+y^{2} \right )-x}$

The given equation is

(x² +y²)² = xy

Differentiating the given equation with respect to x

$\frac{d}{dx}\left ( x^{2}+y^{2} \right )^{2}=\frac{d}{dx}xy$

$2\left ( x^{2}+y^{2} \right ).\left ( 2x+ 2y\frac{dy}{dx}\right )=x\frac{dy}{dx}+y$

$4x\left ( x^{2}+y^{2} \right )+4y\left ( x^{2}+y^{2} \right )\frac{dy}{dx}-x\frac{dy}{dx}=y$

$4y\left ( x^{2}+y^{2} \right )\frac{dy}{dx}-x\frac{dy}{dx}=y-4x\left ( x^{2}+y^{2} \right )$

$\frac{dy}{dx}\left ( 4y\left ( x^{2}+y^{2} \right )-x \right )=y-4x\left ( x^{2}+y^{2} \right )$

$\frac{dy}{dx}=\frac{y-4x\left ( x^{2} +y^{2}\right )}{4x\left ( x^{2}+y^{2} \right )-x}$

Q9. If matrix A is both symmetric and skew symmetric ,then A is necessarily a

(a) Diagonal matrix (b) Zero square matrix (c) Square matrix (d) Identity matrix

Ans.(b) Zero square matrix

Since A is both symmetric and skew symmetric matrix

∴ A = A’ ….(i) and A’ = -A….(ii)

From equation (i) and (ii)

A = -A

A + A = 0

2A = 0

A = 0

Hence A is zero square matrix

Q10. Let set X = {1, 2,3} and a relation R is defined in X as : R = {(1,3),(2,2),(3,2)},then minimum ordered pairs which should be added in relation R to make it reflexive and symmetric are

(a) {(1,1),(2,3),(1,2)} (b) {(3,3),(3,1),(1,2)} (c) {(1,1),(3,3),(3,1),(2,3)} (d) {(1,1),(3,3),(3,1),(1,2)}

Ans.(c) {(1,1),(3,3),(3,1),(2,3)}

The given set is X = {1, 2,3} ,relation R is defined in X as :R= {(1,3),(2,2),(3,2)}

The relation R is reflexive when (1,1),(2,2) and (3,3) ∈R

So, (1,1) and (3,3) must be added to R,to make it reflexive

The relation R is symmetric when (1,3),(3,1) ,( (3,2),(2,3),(2,2) ∈R

So, (3,1) and (2,3) must be added to R,to make it symmetric

Hence to make the relation R reflexive and symmetric ,the minimum ordered pair {(1,1) , (3,3),(3,1) , (2,3)} must be added

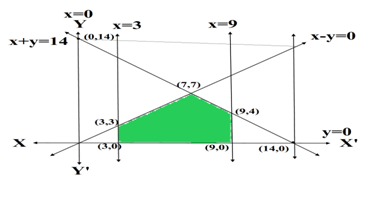
Q11. A linear Programming Problems is as follows :

Minimise z = 2x + y

subject the constraints x ≥3,x≤9,y≥0

x – y ≥0, x + y ≤14

The feasible region has

(a) 5 corner points including (0,0) and (9,5)

(b) 5 corner points including (7,7) and (3,3)

(c) 5 corner points including (14,0) and (9,5)

(d) 5 corner points including (3,6) and (9,5)

Ans.(b) 5 corner points including (7,7) and (3,3)

For minimising z = 2x + y

The given constraints are x ≥3,x≤9,y≥0

x – y ≥0, x + y ≤14

Solving the equations and drawing their graphs

x= 3, x=9,y =0

x -y =0 and x+y =14

Putting x =0

y= 0 and y = -14

5 corner points are (3,0),(9,0),(9,4), (7,7) and (3,3)

Q12. The function f (x)

$f\left ( x \right )=\left\{\begin{matrix} \frac{e^{3x}-e^{-5x}}{x},if\: x\neq 0 & \\ k,if\: x=0 & \end{matrix}\right.$

is continuous at x = 0 for the value of k ,as

(a) 3 (b) 5 (c)2 (d) 8

Ans.(d) 8

LHL of the f(x) at x =0

$\lim_{x\rightarrow 0^{-}}\frac{e^{3x}-e^{-5x}}{x}=\frac{0}{0}$

Applying the L Hospital rule

$=\lim_{x\rightarrow 0}\frac{d/dx (e^{3x}) -d/dx\left ( e^{-5x} \right )}{d/dx\left ( x \right )}$

$=\lim_{x\rightarrow 0}\frac{e^{3x}.3-e^{-5x}\left ( -5 \right )}{1}=3+5=8$

Since the function f (x) is continuous at x = 0

f(0) = k

f(0)= K= LHL =8

Q13. If C_ij denotes the cofactor of element p_ij of the matrix

$P=\begin{bmatrix} 1 & -1 & 2\\ 0 & 2 & -3\\ 3& 2& 4 \end{bmatrix}$

then the value of C₃₁ .C₂₃ is

(a) 5 (a) 24 (a) -24 (a) -5

Ans.(a) 5

Cofafactor C_ij of the element p_ij is expressed as

C_{ij =}(-1)^i+j.det M_ij

Where M_ijis the minor of the element p_ij

C₃₁ – =(-1)³⁺¹.(-3×-1-2×2) =-1

Cofafactor C₂₃ is of the element p₂₃ which is expressed as

C₂₃ =(-1)²⁺³.(2×1-3×-1) =-1(2 +3) =-5

C₃₁.C₂₃=-1(-5) = 5

Q14. The function y = x².e^-xis decreasing in the interval

(a) (0,2) (b) (2,∞) (c) (-∞,0) (d) (-∞,0) ∪(2, ∞)

Ans. The function y is decreasing when

dy/dx <0

Differentiating the given function

dy/dx =d/dx [ x².e^-x]

= x².d(.e^-x)/dx + e^-x.dx²/dx

=x².(-e^-x) + 2x. e^-x

dy/dx=-x²e^-x +2x. e^-x= 0

xe^-x(-x +2) = 0

x (-x +2)=0

x (-x +2)<0

x <0 and -x +2 <0 ⇒ x -2 >0⇒x> 2

∴The function is decreasing in the interval (-∞,0) ∪ (2, ∞) is the

Q15. If R = {(x,y) ; Z, x² + y² ≤ 4} is a relation in set Z, then domain of R is

(a) {0,1,2} (b) {-2,-1,0,1,2} (c) {0,-1,-2} (d) {-1,0,-1}

Ans. (b) {-2,-1,0,1,2}

The given relation in set Z is

R = {(x,y) ; Z, x² + y² ≤ 4}

Since x² + y² ≤ 4

∴For x=0, y² ≤ 4⇒y =0,±1,±2

For x=±1, y²+1 ≤ 4⇒y²≤3⇒y =0,±1

For x=±2, y²+4 ≤ 4⇒y²≤0⇒y =0

The ordered pair of the given relation is given as

R={(0,0),(0,-1),(0,1),(0,2),(0,-2),(-1,0),(1,0),(-1,-1),(1,1),(-1,1),(1,-1),(2,0),(-2,0)}

The domain of R = Set of first element of the ordered pair={0,-1,1,-2,2}={-2,-1,0,1,2}

Q16.The system of linear equations

5x +ky = 5,

3x +3y = 5;

will be consistent if

(a) k ≠ -3 (b) k = -5 (c) k =5 (a) k ≠ -5

Ans.(c) k =5

A pair of linear equations a₁x + b₁y + c₁=0 and a₂x + b₂y + c₂=0 is consistent only when

a₁/a₂ ≠ b₁/ b₂ or a₁/a₂ =b₁ /b₂= c₁/c₂

From the given equation we have

5/3 ≠k/3

3k ≠ 15

k ≠ 5

a₁/a₂ =b₁ /b₂= c₁/c₂

5/3 =k/3 =-5/-5 =1

3k =15 ⇒k=5 and k =3

Q17.The equation of the tangent to the curve y(1 +x²) = 2 – x,where it crosses the x -axis is

(a) x -5y =2 (b) 5x – y =2 (c) x + 5y = 2 (d) 5x + y =2

Ans.(c) x + 5y = 2

The given curve

y(1 +x²) = 2 – x

$\frac{d}{dx}\left [ y\left ( 1+x^{2} \right ) \right ]=-1$

$y\frac{d}{dx}\left ( 1+x^{2} \right )+\left ( 1+x^{2} \right )\frac{dy}{dx}=-1$

$y.2x+\left ( 1+x^{2} \right )\frac{dy}{dx}=-1$

$\left ( 1+x^{2} \right )\frac{dy}{dx}=-1-2xy$

$\frac{dy}{dx}=\frac{-1-2xy}{1+x^{2}}$

The curve y(1 +x²) = 2 – x crosses the x-axis

Putting the value y=0

0(1 +x²) = 2 – x

2 – x =0

x =2

Slope of the tangent at (2,0) = (-1-2×2×0)/(1+2²) =-1/5

The equation of the tangent

y – 0 = (-1/5)(x -2)

5y = -x +2

x +5y =2

You can compensate us by donating any amount of money for our survival

Our Paytm No 9891436286

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions of class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions of class 9 science

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

CBSE Class 9-Question paper of science 2020 with solutions

CBSE Class 9-Sample paper of science

CBSE Class 9-Unsolved question paper of science 2019

NCERT Solutions of class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT solutions of class 10 science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

Solutions of class 10 last years Science question papers

CBSE Class 10 – Question paper of science 2020 with solutions

CBSE class 10 -Latest sample paper of science

NCERT solutions of class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT solutions of class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals