Class 10 Maths Sample Paper(Standard) for 2021 CBSE Board Exam -Term 1 with Solutions

Class 10 Maths Sample Paper(Standard) for 2021 CBSE Board Exam -Term 1 with Solutions created here for helping the students to boost their preparation for the exam of term 1 Class 10 CBSE board which is going to be held on november -december 2021.Class 10 Maths Sample Paper(Standard) for 2021 CBSE Board Exam -Term 1 with Solutions is the reference from CBSE Board circular no-Acad 75/2021 dated 02-09-2021 regarding sample paper for CBSE board Examination.

You can download the pdf of the solutions of all the MCQs

Download PDF-Class 10 Maths Sample Paper(Standard) for 2021 CBSE Board Exam -Term 1 with Solutions

Pdf of Solutions-Class 10 Maths Sample Paper for Term 1 2021

For extra practice you can download our e-book with solutions of class 10 maths last years 4 question papers.

Download -PDF for cllass 10 solutions of last year’s maths question papers

Class 10 Maths Sample Paper(Standard) for 2021 CBSE Board Exam -Term 1 with Solutions

Q1. The ratio of LCM and HCF of the least composite and the least prime numbers is

(a) 1 : 2     (b) 2 : 1   (c) 1 : 1    (d) 1 : 3

Ans. (b) 2 : 1

Explanation. The least composite number is 4 and the least prime number is 2

HCF(4,2) = 2 and LCM(4,2) = 4

Ratio of LCM(4,2) : Ratio of HCF(4,2) = 4 : 2 = 2 : 1

Q2.The value of k for which the lines 5x + 7y =3 and 15x +21 y = k coincide is

(a) 9    (b) 5    (c) 7   (d)  18

Ans.(a) 9

Explanation. The  lines a₁x + b₁y + c₁ =0 and a₁x + b₁y + c₁ =0  coincide to each other when

The given equations are 5x + 7y =3 and 15x +21 y = k

Arranging the equations into the standard equation

5x + 7y – 3 =0 and 15x +21 y – k =0

5k = 15 ×3 =45

k = 45/5 = 9

See the video -Complete solutions of Pre-board class 10 Maths Exam for Term 1 2021 

Q3. A girl walks 200 m towards east and then 150m towards north .The distance of the girl from the starting point is

(a) 350 m     (b) 250m       (c) 300m      (d) 225m

Ans. (b) 250 m

 

 

 

 

 

 

Let initial point of the girl is A ,she walks 200m towards the east upto B point and then turn 150 m towards the north upto C

Therefore the distance of the girl from the initial point is = AC

The triangle ABC so formed is a right triangle,so applying pythogorus theorem

AC² =AB² + BC² = 200² +150² = 40000 + 22500

AC² = 62500

AC =√62500

AC = 250

Hence the distance of the girl from the starting point is 250 m

Q4. Length of the diagonals of a rhombus are 24 cm and 32 cm,then the length of the altitude of the rhombus is

(a) 12 cm     (b) 12.8 cm      (c) 19 cm     (d) 19.2 cm

Ans.

 

 

 

 

 

 

Since the diagonal of the rhombus bisect each other at 90°, therefore ΔAOB is a right triangle

So, AB² =OA² + OB² = 16² +12²=256 +144

AB² = 400

AB =√400 = 20

Area of the rhombus = Base × Atitude =AB ×h = 20h

The area of the rhombus = (1/2) (Product of the diagonals)= (32×24)/2=384 cm²

20h =384

h = 384/20 = 19.2

Hence altitude of the rhombus is 19.2 cm

Class 10 Maths Sample Paper(Standard) for 2021 CBSE Board Exam -Term 1 with Solutions

Q5.Two fair coins are tossed .What is the probability of getting at the most one head ?

(a) 3/4      (b) 1/4       (c) 1/2     (d) 3/8

Ans. (a) 3/4

When two fair coins are tossed,then the total outcomes are (HH,TT,HT,TH)

The favourable outcomes are = At the most one head(i.e one head and less than 1 head)

So,the favourable outcomes are (TT,HT,TH)

∴ P(at the most one head) = 3/4

Q6.ΔABC ∼ΔPQR,If AM and PN are altitudes of ΔABC and ΔPQR respectively and AB² : PQ²=4: 9,then AM : PN =

Ans. We know the corresponding sides and medians of two similar triangles are in proportion

AB/PQ = BC/QR =AC/PR = AM/PN….(i)

We are given AB² : PQ²=4: 9

AB² / PQ²=4/ 9

AB/PQ = 2 / 3

Therefore  from equation (i) AM /PN = 2 /3

Q7. If 2 sin²β -cos²β =2,then β is

(a) 0°     (b) 90°    (c) 45°    (d) 30°

Ans. We are given

2 sin²β -cos²β =2

2(1-cos²β) -cos²β =2 (since sin²θ = 1- cos²θ)

2 -2cos²β -cos²β = 2

-3cos²β = 0

cosβ =0 =cos 90°

β =90°

Q8.Prime factors of the denominator of a rational number with the decimal expansion 44.123 are

(a) 2 ,3      (b) 2,3,5     (c) 2,5     (d) 3,5

Ans. (c) 2,5

The decimal expansion of the given rational number is 44.123

44.123 = 44123/1000 =44123 /10³= 44123/(2×5)³

Hence the prime factors of the denominator are 2,5

Q9. The lines x = a and y =b, are 

(a) Intersecting    (b) Parallel      (c) Overlapping   (d) Non-of these

Ans (a) Intersecting

The given lines x =a and y =b are drawn graphically as below.

 

 

 

 

 

 

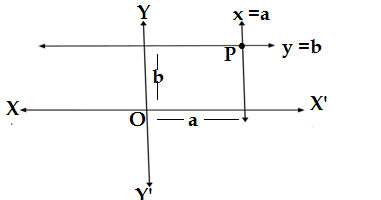
It is clear from the figure that both lines intersect at P

Q10.The distance of the point A(-5,6) from the origin is

(a) 11 units     (b) 61 units      (c) √11 units     (d) √61 units

Ans. (d) √61 units

The coordinates of the origin are (0,0) and the given point is (-5,6)

We know the distance (d) between (x₁,y₁) and (x₂,y₂) is

d = √[(x₂-x₁)²+(y₂-y₁)²] =√[(-5-0)²+(6-0)²] =√[(-5)²+6²] =√(25 +36) =√61

Q11.If a² = 23/25,then a is

(a) rational     (b) irrational     (c) whole number   (d) integer

Ans. (b) irrational

We are given

a² = 23/25

a =√(23/25) = √23/5

√23 is irrational number and 5 is rational

An irrational number divided by a rational number results an irrational number

See the video for Answers of The questions from Q1-Q11

Q12. If LCM(x,18) =36 and HCF(x,18) =2,then x is

(a) 2         (b) 3        (c) 4        (d) 5

Ans.(c) 4

We know

LCM × HCF = Product of the numbers

The numbers given to us are x and 18,and their LCM =36,HCF =2

So,

36×2 = 18x

72 = 18x

x = 72/18 =4

Class 10 Maths Sample Paper(Standard) for 2021 CBSE Board Exam -Term 1 with Solutions

Q13. In ΔABC right angled at B,if tan A = √3,then cos A cos C – sin A sin C =

(a) -1       (b) 0         (c) 1           (d) √3/2

Ans.(b) 0

 

 

 

 

 

 

We are given

tan A = √3⇒ P/B =BC/AB =√3/1

H = √(P² + B²) =AC=√(BC²+AB²)=√[(√3)² +1²) =√(3+1) =√4 =2

cos A =AB/AC = 1/2, cos C =BC/AC =√3/2, sin A =BC/AC =√3/2, sin C = AB/AC= 1/2

Putting the values in

cos A cos C – sin A sinC= (1/2)(√3/2) – (√3/2)(1/2) =√3/4  – √3/4 =0

Q14.  the angle sum property of the triangle)

4x =180°If the angles of a ΔABC are in the ratio 1 : 1 : 2, respectively( the largest angle being angle C) ,then the value of (sec A/cosec B) – (tan A/cot B) is

(a) 0      (b) 1/2       (c) 1        (d) √3/2

Ans. (a) 0

Let the angles of the given triangle are x,x and 2x

x + x +2x =180° (As per

x = 180°/4 = 45

∴ ∠A = 45°, ∠B =45° and ∠C = 2x =2×45=90°

Putting the values of all angles in the expression  (sec A/cosec B) – (tan A/cot B) is

(sec 45°/cosec 45°) – (tan 45°/cot 45)

=(√2/√2 ) -(1/1)

=1 -1 = 0

Q15. The number of revolutions made by a circular wheel of the radius 0.7 m in rolling a distance of 176 m is

(a) 22          (b) 24          (c) 75       (d) 40

Ans. (d) 40

The distance covered by the wheel in one revolution = Circumference of the wheel

Circumference of the wheel = 2πr = 2×(22/7)×0.7 =4.4 m

Number of revolutions = Distance/Distance covered in one revolution =176/4.4 =40

Q16.ΔABC is such that AB = 3cm, BC = 2 cm, CA = 2.5 cm. If ΔABC ∼ΔDEF and EF = 4 cm,then perimeter of the ΔDEF is

(a) 7.5 cm       (b) 15 cm       (c) 22.5 cm     (d) 30 cm

Ans. (b) 15 cm

We are given ΔABC ∼ΔDEF

According to the rule of similarity of the triangles

AB/DE = BC/EF = CA/DF

3/DE = 2/4 = 2.5/DF

Taking

3/DE = 2/4

2DE =12

DE = 12/2 = 6 cm

Taking

2/4 = 2.5/DF

2DF = 2.5×4 =10

DF =10/2 = 5 cm

Now, we have EF = 4cm, DE = 6 cm and DF = 5 cm

Perimeter of ΔDEF = 4 + 6 + 5 = 15 cm

Subscribe our Utube channel

Q17.In the figure if DE ∥ BC,AD = 3 cm,BD = 4 cm and BC = 14 cm, then DE =

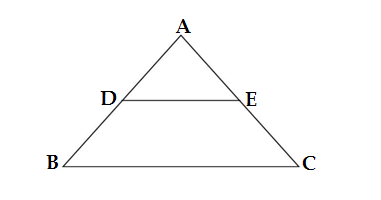
(a) 7 cm      (b) 6 cm       (c) 4 cm      (d) 3 cm

Ans. (b) 6 cm

It is given to us DE ∥ BC

∠A = ∠A (common)

∠ADE =∠B (corresponding angle)

ΔABC ∼ΔADE (AA rule)

Applying the rule of similarity

AB/AD = BC/DE = AC/AE

(3+4)/3 = 14/DE

14/DE = 7/3

7DE = 14×3 =42

DE = 42/7 =6 cm

Class 10 Maths Sample Paper(Standard) for 2021 CBSE Board Exam -Term 1 with Solutions

Class 10 Maths MCQ -Trigonometry for Term 1 CBSE 2021

Q18.If 4 tan β =3, then

(a) 0      (b) 1/3       (c) 2/3      (d) 3/4

Ans. (a) 0

We are given that

4 tan β =3

tan β =3/4 =P/B

∴ H= √(P² +B²) = √(3² +4²)=√(9 +16)=√25 = 5

sin β = P/H = 3/5, cos β = B/H = 4/5

Q19.One equation of a pair of dependent linear equations is -5x +7y =2. The second equation can be

(a) 10x +14y +4 =0    (b) -10x -14y +4 =0   (c) -10x +14y +4 =0   (d) 10x -14y =-4

Ans. (d) 10x -14y =-4

Two equations are called dependent on each other if their coeffiecients are multiple of each other.

The given equation is –5x +7y =2, observing all equations, we get equation (d) 10x -14y =-4 is a dependent equation of the given equation because if we divide equation (d) by -2,we get -5x +7y =2

Q20. A letter of english alphabets is chosen at random .What is probabilty that it is a letter of the word ‘Mathematics’

(a) 4/13      (b) 9/26      (c) 5/13     (d) 11/26

Ans. (a) 4/13

Total letters in the english alphabets are = 26

The letters in the word ‘Mathematics’ are (m,a,t,h,e,i,c,s)

P(letter in the word ‘Mathematics’) = 8/26 = 4/13

Class 10 Maths Sample Paper(Standard) for 2021 CBSE Board Exam -Term 1 with Solutions

Section-B

Q21. If the sum of two numbers is 1215 and their HCF is 81, then the possible number of pairs of such numbers are 

(a) 2        (b) 3       (c) 4          (5) 5

Ans. (c) 4

The given HCF of both numbers is=81

Since the numbers are multiple of their HCF, so let the numbers are 81x and 81y where x and y are coprime numbers

The sum of the number is given =1215

81x + 81y = 1215

x + y = 1215/81 =15

If x =1 then y =14 if x is 2 then y =13, if x =4 then y =11,if x =7 then y =8

Q22.Given below is the graph representing two linear equations by lines AB and CD respectively .What is the area of the triangle formed by these two lines and the line x =0

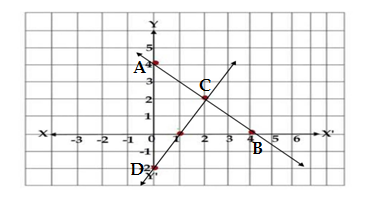
(a) 3 sq. units      (b) 4 sq.units      (c) 6 sq.units       (d) 8 sq.units

Ans. The line shown in the graph are AB and DC, which are intersecting at C(2,2) and the line x =0(i.2 Y axis) at A(0,4) and D(0.-2)

The triangle formed by the lines and x =0 is ΔADC

The altitude of the ΔADC  is the distance of C from the base AD = 2 units and the length of the base is 4 -(-2) = 4+2 = 6 units

Area of the ΔADC = (1/2) ×6×2 = 12/2 = 6 sq.units

Q23. If tan α + cot α =2, then tan²⁰α + cot²⁰α =

(a) 0       (b) 2        (c) 20       (d) 2²⁰

Ans. (b) 2

We are given

tan α + cot α =2

Simplifying it

tan α + 1/tan α =2

(1 +tan ²α)/tan α =2

tan²α  +1 =2 tan α

tan ²α -2 tanα +1 = 0

(tan α -1)² =0

tan α -1 =0

tan α = 1

Therefore tan²⁰α + cot²⁰α =

1²⁰ + 1²⁰ = 1 +1 =2

Q24. If 217x + 131y = 913,131x + 217y =827,then x +y is

(a) 5      (b) 6      (c) 7       (d) 8

Ans.(a) 5

The given equations are 217x + 131y = 913……(i) 131x + 217y =827….(ii)

Adding both of the equations (i) and (ii)

348x + 348y = 1740

348(x +y) =1740

x +y = 5

Class 10 Maths Sample Paper(Standard) for 2021 CBSE Board Exam -Term 1 with Solutions

Q25. The LCM of two prime numbers is p and q (p > q) is 221 . Find the value of 3p – q

(a) 4      (b) 28     (c) 38       (d) 48

Ans. (c) 38

Prime factors of 221 = 13×17

Since it is given to us that p > q, so p =17 and q=13

3p -q =3×17 – 13 = 51 -13 = 38

Q27. A card is drawn from a well-suffled deck of cards . What is the probability that the card drawn is neither a king nor a queen ?

(a) 11/13     (b) 12/13     (c) 11/26     (d) 11/52

Ans.(a) 11/13

The total cards are 52,so total outcomes are =52

The number of queens are 4 and number of kings are 4, favourable outcomes are 52 -8 =44

P(neither a king nor a queen) = 44/52 = 11/13

Q27. Two fair dice are rolled simultaneously .The probability that 5 will come up at least once is 

(a) 5/36      (b) 11/36     (c) 12/36     (d) 23/36

Ans.(b) 11/36

When two fair dice are rolled then total possible outcomes are 36

Favourable outcomes are ⇒ 5 will come up at least once

∴Favourable outcomes of this event are (1,5),(2,5),(3,5),(4,5),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,5),hence favourable outcomes are 11

P( 5 comes up at least once) = 11/36

Q28. If 1 + sin²α = 3 sin α cos α,then values of cot α are

(a) -1,1     (b) 0,1    (c) 1,2    (d) -1,-1

Ans. We are given that

1 + sin²α = 3 sin α cos α

sin²α + cos²α + sin²α = 3 sin α cos α

2 sin²α -3 sin α cos α + cos²α = 0

2 sin²α -2sin α cos α- sin α cos α+ cos²α = 0

2 sin α( sin α -cos α) -cos α( sin α – cos α) = 0

( sin α -cos α) ( 2 sin α -cos α) = 0

sin α -cos α= 0

sin α = cos α

cos α /sin α =1

cot α  = 1

Taking

2 sin α -cos α= 0

2 sin α = cos α

cos α/sin α  =2

cot α =2

Hence the values of cot α are 1,2

Q29. The vertices of a parallelogram in order are A(1,2),B(4,y),C(x,6) and D(3,5). Then (x,y) is

(a) (6,3)      (b) (3,6)       (c) (5,6)      (d) (1,4)

Ans.(a) (6,3)

The vetrtices of the parallogram are given in order A(1,2),B(4,y),C(x,6) and D(3,5)

Therefore parallogram is ABCD, where AC and BD are the diagonals

AC and BD bisect each other,therefore their mid points coincide to each other

The coordinates of the mid point of AC = Coordinates of the mid point of BD

(1 +x)/2, (2 +6)/2 = (4 +3)/2, (y +5)/2

(1 +x)/2 , 4      = 7/2,  (y+5)/2

(1 +x)/2 =7/2

x +1 =7

x = 7-1 =6

(y+5)/2 =4

y +5 = 8

y =8-5 =3

Hence the value of x is 6 and of y is 3,so the (x,y) are (6,3)

You can also see Utube video-Class 10 Maths Preboard-2 Question Paper(Standard) for 2021-22 CBSE Board Exam -Term 1 with Solutions

Q30. In the given figure ∠ACB =∠CDA ,AC = 8 cm,AD =3 cm,then BD is

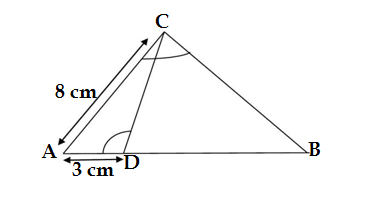
(a) 22/3     (b) 26/3      (c) 55/3     (d) 64/3

Ans.(c) 55/3

From the figure

In ΔABC and ΔADC

∠ACB =∠CDA (given)

∠A = ∠A (common)

ΔABC ∼ ΔACD (AA rule)

According to the rule of similarity

AB/AC = BC /CD = AC /AD

AB/8 = 8/3

3AB = 8×8 =64

AB = 64/3

BD = AB -AD = 64/3  -3 = (64 -9)/3 = 55/3

Q31. The equation of the perpendicular bisector of line segment joining points A(4,5) and B(-2,3) is

(a) 2x -y +7 = 0     (b) 3x + 2y -7 =0     (c) 3x – y -7 =0    (d) 3x + y-7 =0

Ans.(d) 3x + y -7 =0

Let the mid point of the line segment  joining A(4,5) and B(-2,3)

Perpendicular bisector is equidistant from the point A and point B

√[(x -4)² + (y -5)²] = √[(x +2)² + (y -3)²]

Squaring both sides

(x -4)² + (y -5)² = (x +2)² + (y -3)²

x² + 16 -8x + y² + 25 -10y = x² + 4 + 4x + y²+9 -6y

-8x -10y +41 = 4x -6y +13

-8x -4x -10y +6y =13 -41 = -28

-12x -4y =-28

3x + y =7

3x + y -7 =0

Q32. In the given figure ,D is the mid point of BC , then the value of cot y°/ cot x° is

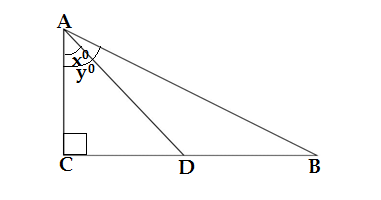
(a) 2       (b) 1/2        (c) 1/3      (d) 1/4

Ans. (b) 1/2

AC ⊥BC and AC ⊥ DC,so ΔACD and ΔACB are the right triangles

cot y° = B/P = AC/BC….(i)

cot x° = B/P = AC/DC = AC/(BC/2) = 2AC/BC….(ii)

From equations (i) and (ii)

cot y°/cot x°  = (AC/BC)/(2AC/BC) = (AC/2AC).BC/BC = 1/2

Utube Video-Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22

Q33. The smallest number by which 1/13 should be multiplied so that its decimal expansion terminates after two decimal places is 

(a) 13/100      (b) 13/10      (c) 10/13     (d) 100/13

Ans. (a) 13/100

The number given to us is 1/13

For terminating decimal, the factor of the denominator should be in the form of 2ⁿ × 5ⁿ

For, this first of all eliminate the denominator by multiplying 13, and dividing it by 100 so that number terminates up to 2 places

1/13 ×13/100= 1/100 = 0.01

Q34.Sides AB and BE of a right triangle, right-angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of the largest square FDGB that can be inscribed in the triangle ABE is

(a) 32/3 cm     (b) 16/3 cm     (c) 8/3 cm     (d) 4/3 cm

Ans.(b) 16/3

The given triangle is ABE ,in which largest square FDGB is inscribed

Let the length of the square is x

So,BG = FD =x

∠ADF =∠DEG (corresponding angle)

∠AFD =∠DGE =90°(FD⊥AF and DG ⊥GE)

ΔAFD ∼ΔDGE(AA rule)

Applying the rule of similarity

AF/DG =FD/GE

(16 -x)/x =x/(8-x)

(16 -x)(8-x) = x²

128 -16x -8x +x²=x²

24x =128

x = 128/24 =16/3

Class 10 Maths Sample Paper(Standard) for 2021 CBSE Board Exam -Term 1 with Solutions

Q35. Point P divides the line segment joining R(-1,3) and S(9,8) in ratio k : 1. If P lies on the line x -y +2 =0,then value of k is

(a) 2/3      (b) 1/2     (c) 1/3     (d) 1/4

Ans. (a) 2/3

It is given to us taht point P divides the line segment joining two points R(-1,3) and S(9,8) in ratio k : 1

Applying the section formula

x =(mx₂+nx₁)(m+n), y=(my₂+ny₁)(m+n)

Where (x,y) is the point P, m : n = k : 1, (x₁,y₁) =(-1,3) and (x₂,y₂) =(9,8)

x =(9k-1)/k+1), y =(8k+3)/k+1)

Therefore coordinates of the point P are [(9k-1)/k+1), (8k+3)/k+1)]

Since point P lies on the line x -y +2 =0,so the coordinates of point P should satisfy the equation

(9k-1)/k+1) -(8k+3)/k+1) +2 =0

9k -1 -8k -3 +2k +2 =0

3k -2 =0

3k =2

k =2/3

Q36. In the figure given below ,ABCD is a square of side 14 cm with E ,F,G and H as the mid points of AB,BC,CD and DA respectively. The area of the shaded portion is

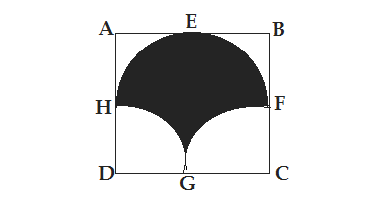
(a) 44 cm²     (b) 49 cm²    (c) 98 cm²    (d) 49π/2 cm²

Ans.(c) 98 cm²

Area of shaded portion =Area of semicircle HEF + Area of HFG

Area of shaded portion HFG =Area of the rectangle HFCD -Area of two-quadrant HGD and FGC =7×14 -2×(1/4)πr² (r=7) = 98 -(22/7)(1/2)×7×7 =98 -77 =21 cm²

Area of the shaded semicircle HEF  is =( 1/2)π×r² (where r=7, is half of the side of the square)

=(22/14)×7×7 =77 cm²

Area of shaded portion = 21 + 77 =98 cm²

Q37. Given below is the picture of Olympic rings made by taking five congruent circles of radius 1 cm each , intersecting in such a way that the chord formed by joining the point of intersection of two circles is also of length 1 cm. The total area of all the dotted regions assuming the thickness of the rings to be negligible is

 

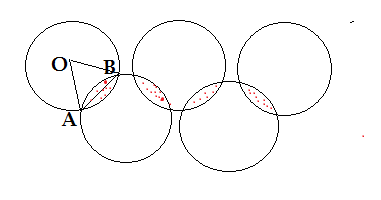
(a) 4(π/12 -√3/4) cm²    (b) (π/6 -√3/4) cm²   (c) 4(π/6 -√3/4) cm²  (d) 8(π/6-√3/4) cm²

Ans.(d) 8(π/6-√3/4)

The length of the chord is =1 cm, length of the radii of the circles is =1 cm

Joining A and B to the centre of circle,we get an equilateral triangle ABO of the side 1 cm

Area of the minor segment = Area of minor  sector AOB-Area of ΔAOB

Area of ΔAOB = side²(√3/4) ( side =1 cm) = 1²×√3/4 =√3/4

Area of minor sector = (60°/360°)×πr² = (1/6)π×1²=π/6 cm²

Area of the minor segment = (π/6- √3/4) cm²

Since chord drawn in the circle divides the dotted portion in two equal parts

Therefore area of the dotted portion =2 (π/6-√3/4) cm²

The area of 4 dotted portion =4×2(π/6-√3/4) =8(π/6-√3/4)

Q38. If 2 and 1/2 are the zeroes of px² + 5x + r,then

(a) p =r =2     (b) p =r =-2     (c) p = 2 ,r =-2    (d) p =-2, r =2

Ans.(b) p = r =-2

In a quadratic equation ax² +bx + c=0,the relationship between coefficients and the zeroes (α and β) are as follows

α + β = -b/a and α β = c/a

The given equation is px² + 5x + r

2 +1/2 = -5/p

5/2 = -5/p

p = -5×2/5 = -2

2(1/2) = r/-2

r =-2

Hence p=r =-2

Q39.The circumference of a circle is 100 cm. The side of a square inscribed in the circle is

(a) 50√2 cm     (b) 100/π cm     (c) 50√2/π  cm  (d) 100√2/π cm

Ans.(c) 50√2/π cm

The circumference of the circle is =2πr =100 ⇒r = 100/2π

Since the square is inscribed in the circle

Therefore the radius of the circle = half of the diagonal of the square =100/2π

Diagonals of the square bisect each other at 90°

∴ Side of the square =√[(100/2π)² +(100/2π)²]=√2(100/2π)²)=√2(10000/4π²) =50√2/π cm

Class 10 Maths Sample Paper(Standard) for 2021 CBSE Board Exam -Term 1 with Solutions

Q40.The number of solutions of 3^x+y=243  and 243^x+y =3 is

(a) 0       (b) 1          (c) 2     (d) infinite

Ans.(a) 0

We are given the equations 3^x+y=243  and 243^x+y =3

Factorizing 243

243 = 3×3×3×3×3 = 3⁵

Substituting 243 =3⁵ in both of the equations

3^x+y=3⁵ and( 3⁵)^x+y =3

x + y =5 …(i) and 5x +5y =1…(ii)

From (i) and (ii), we have

1/5 =1/5 ≠-5/-1

Therefore the given equations have infinite solutions

Class 10 Maths Sample Paper(Standard) for 2021 CBSE Board Exam -Term 1 with Solutions

Section-C

Q41 -Q45 are based on Case Study I

The figure given alongside shows the path of a diver ,when she takes a jump from the diving board .Clearly it is a parabola.

Anni was standing on a diving board ,48 feet above the water level. She took a dive into the pool. Her height (in feet) above the water level at any time ‘t’ in seconds is given by the polynomial h(t) such that

h(t) =-16 t²+8t + k

Q41. What is the value of k?

(a) 0       (b) -48     (c) 48     (d) 48/-16

Ans.(c) 48

Inially Anni was standing on a diving board which is 48 above the water level

So,at time ,t =0 the height is 48 feet

h(0) = 16 ×0² +8×0 +k

48 =k

Q42. At what time  will she touch the water in the pool ?

(a) 30 seconds     (b) 2 seconds     (c) 1.5 seconds    (d) 0.5 seconds

Ans.(b) 2 seconds

Let she touch the water in the pool in t time

Since at t=0,her height above the water level was 48 feet,so after t time ,her height above the water level will be 0, means h(t) =0

So,

-16 t²+8t + k =0

16t² -8t -48 =0

2t² -t -6 =0

2t² -4t +3t -6 =0

2t(t -2) +3(t -2) =0

(2t +3)(t-2) =0

Taking 2t +3=0⇒t =-3/2 and t-2 =0⇒t =2

Neglecting negative root because time can’t be negative,therefore time taken by Annie to reach the water level is 2 seconds

Q43. Rita’s height (in feet) above the water level is given by another polynomial p(t) with zeroes -1 and 2. Then p(t) is given by-

(a) t² +t -2      (b) t² +2t -1   (c)24t² -24t +48    (d) -24t² +24t +48

Ans.(c)24t² -24t +48

The quadratic(i.e of power 2) polynomial p(x) with zeroes α and β is given as

p(x)=x² – (α + β)x + αβ

α =-1 and β=2

∴ p(t) = t² -(-1 +2)t + 2×-1

p(t) = t² -t – 2

If we multiply the polynomail by 24(constant) then polynomial is not effected

24p(t) = 24t² -24t – 48

p(t) = 24t² -24t – 48

Hence the required polynomial is  24t² -24t – 48

Q44. A polynomial q(t) with sum of zeroes as 1 and the product as -6 is modelling Anu’s height in feet above the water at any time t(in seconds). Then q(t) is given by

(a) t² +t +6      (b) t² +t -6   (c)-8t² +8t +48    (d) 8t² -8t +48

Ans.(c) -8t² +24t + 48

The quadratic(i.e of power 2) polynomial p(x) with zeroes α and β is given as

p(x)=x² – (α + β)x + αβ

The sum of the zeroes and the product of zeroes given to us ,

α + β =1 and  αβ =-6

q(t)=t² – t + (-6)

q(t) =t² – t -6

If we multiply the polynomail by -8(constant) then polynomial is not effected

-8p(t) = -8t² +24t + 48

Hence the required polynomial is -8t² +24t + 48

Q45. The zeroes of the polynomial r(t) =-12t² +(k-3)t +48 are negative of each other.Then k is

(a) 3       (b) 0      (c) -1.5        (d) -3

Ans.(a) 3

Let one of the zeroes of the given polynomial -12t² +(k-3)t +48 is α then other is -α

The relationship between the coefficients and the zeroes of the polynomial is given by

α +β = -b/a and αβ = c/a

α -α =-(k-3)/-12

0 =(k-3)/12

k-3 =0

k =3

Hence the value of k is 3

Case Study-2

A hockey field is the playing surface for the game of hockey. Historically, the game was played on natural turf (grass) but nowadays it is predominantly played on an artificial turf.

It is rectangular in shape – 100 yards by 60 yards. Goals consist of two upright posts placed equidistant from the centre of the backline, joined at the top by a horizontal crossbar. The inner edges of the posts must be 3.66 metres (4 yards) apart, and the lower edge of the crossbar must be 2.14 metres (7 feet) above the ground.

Each team plays with 11 players on the field during the game icluding the goalie.

Positions you might play include-

• Forward: As shown by players A,B,C and D
• Midfielders: As shown by players E,F and G
• Fullbacks: As shown by players H,I and J
• Goalie: As shown by player K

Using the picture of a hocky field below ,answer the questions that follow.

Q46.The coordinates of the centroid of ΔEHJ are

(a) (-2/3,1)    (b) (1,-2/3)     (c) (2/3,1)    (d) -2/3,-1)

Ans.(a) (-2/3,1)

The vertices of ΔEHJ are  E(2,1),H(-2,4) and J(-2,-2)

The centroid of the triangle is =[(2-2-2)/3,(1+4-2)/3]=(-2/3,1)

Q47.If a player needs to be at equal distances from A and G,such that A,P and G are in straight line ,then position of P will be given by

(a) (-3/2,2)    (b) (2,-3/2)     (c) (2,3/2)    (d) (-2,-3)

Ans.(c) (2,3/2)

The position of player A(3,6) and of player G(1,-3)

A,P and G are in straight line and P is equidistant from A and G,means P is the mid point od A and G

Coordinates of P = [(3+1)/2,(6-3)/2]=(4/2,3/2) =(2,3/2)

Hence position of P is (2,3/2)

Q48.The point on x axis equidistant from I and E is

(a) (1/2,0)    (b) (0,-1/2)     (c) (-1/2,0)    (d) 0,1/2)

Ans.(a) (1/2,0)

Let the point on axis is (x,0) equidistant from I and E

The coordinates of E are (2,1) and of I are (-1,1)

√[(x-2)² +(0-1)²]=√[(x+1)² +(0-1)²]

(x-2)² +(0-1)²=(x+1)² +(0-1)²

x² +4-4x +1 =x² +1 +2x +1

-4x -2x +5 -2 =0

-6x +3 =0

-6x =-3

x = -3/-6 = 1/2

Hence the required point on x axis is (1/2,0)

Q49.What are the coordinates of the position of a player Q such that his distance from k is twice his distance from E and K,Q and E are collinear?

(a) (1,0)    (b) (0,1)     (c) (-2,1)    (d) (-1,0)

Ans.(b) (0,1)

It is given that K,Q and E are collinear

Let the coordinates of Q are (x,y)

Distance of player Q from K =2×Distance of player Q from E

KQ = 2QE

KQ/QE =2/1⇒ KQ : QE =2: 1

The points are K(-4,1),E(2,1)

Applying section formula

x = (2×2-4)(2+1) and y =(2×1+1×1)(2+1)

x =(4-4)/3 and y =(2+1)/3

x =0 and y =1

Hence the position of the player Q is (0,1)

Q50.The point on Y axis equidistant from B and C is

(-1,0)    (b) (0,-1)     (c) (1,0)    (d) (0,1)

Ans.(d) (0,1)

Let point  on y-axis is (0,y)

Sice point (0, y) is eqidistant from points B(4, 3) and C(4, -1)

Squaring both sides

The distance of the point (0,y) and (4,3) =The distance of the point (0,y) and C(4,-1)

√[(4-0)²+(y-3)²]=√[(4-0)²+(y+1)²]

4² + (y – 3)² = 4² + (y + 1)²

(y – 3)² = (y + 1)²

y² + 9 – 6y = y² + 1 + 2y

9 – 6y = 1 + 2y

9 – 1 = 2y + 6y

8 = 8y

y = 8/8

y = 1

∴ Required coordinates on Y axis = (0, y) = (0, 1)

So, the correct answer is (d)

You can compensate us by donating any amount of money for our survival

Our Paytm No 9891436286

NCERT Solutions of  Science and Maths for Class 9,10,11 and 12

NCERT Solutions of class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions of class 9 science 

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

CBSE Class 9-Question paper of science 2020 with solutions

CBSE Class 9-Sample paper of science

CBSE Class 9-Unsolved question paper of science 2019

NCERT Solutions of class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

The following links are also useful for class 10 maths extra preparation of the CBSE board exams

Class 10 Maths Sample Paper (Basic) with Solutions for Term 1 CBSE Board Exam 2021-22

Class 10 Maths Question paper(Basic) 2021 CBSE preboard Board Exam

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

NCERT solutions of class 10 science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

Solutions of class 10 last years Science question papers

CBSE Class 10 – Question paper of science 2020 with solutions

CBSE class 10 -Latest sample paper of science

NCERT solutions of class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT solutions of class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals