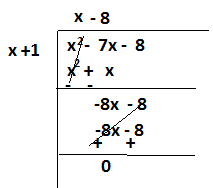Skip to content 
Class 10 Maths Sample Paper (Basic) with Solutions for Term 1 CBSE Board Exam 2021-22
Class 10 Maths Sample Paper (Basic) with Solutions for Term 1 CBSE Board Exam 2021-22 is created here for the students of class 10 CBSE students who are going to appear in Term -1 CBSE Board Exam 2021. Class 10 students of the CBSE Board are required to study MCQ questions that are going to be asked in the 2021 years CBSE Board Exams. The solution of each question is solved by an expert of Maths.The solutions of Class 10 Maths Sample Paper (Basic) with Solutions for Term 1 CBSE Board Exam 2021-22 is presented here for guiding the students of 10 class so that they could get an idea of solving Term 1 Maths (Basic) question paper 2021.
Class 10 Maths(Basic) Sample Paper Term 1 CBSE Board 2021-22 with Solutions
Class 10 Maths(Basic) Preboard Exam (First) 2021-22 CBSE with Solutions
MCQ’s on Real Numbers for Term 1 CBSE with Solutions
MCQ’s on Class 10 Maths Co-ordinate Geometry for Term 1 CBSE
Class 10 Maths MCQ’s on Trigonometry for Term 1 CBSE with Solutions
Class 10 MCQ’s questions with solutions-Polynomial
Class 10 Maths Sample Paper (Basic) with Solutions for Term 1 CBSE Board Exam 2021-22
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
SECTION A
Q1.A box contains cards numbered 6 to 50 . A card is drawn fro the box. The probability that the drawn card has a number which is a perfect square like 4,9…. is
(a) 1/45 (b) 2/15 (c) 4/45 (d) 1/9
Ans. (d) 1/9
The number of cards are from 6 to 50
Total number of cards are = 50 -6 +1 = 45
The numbers which are perfect square between 6 to 50 are 9,16,25,36,49 (i.e 5)
P( card drawn is perfect square ) = number which are perfect square between 6 to 50/total numbers from 6 to 50
= 5/45 = 1/9
Q2.In a circle of diameter 42 cm,if an arc subtends an angle 60° at the centre where π = 22/7,then the length of the arc is
(a) 22/7 cm (b) 11 cm (c) 22 cm (d) 44 cm
Ans.(c) 22 cm
The diameter of the circle is =42 cm,therefore its radius,r =42/2 = 21 cmm
Angle subtended by an arc at the centre is,θ = 60°
The length of an arc ,l = θ/360°×2πr = (60°/360°)×2×(22/7)×21 =22 cm
Q3.If sin θ = x and sec θ = y , then tan θ is
(a) x (b) x/y (c) y/x (d) 1/xy
Ans. (b) x/y
We are given x = sin θ and y = sec θ
tan θ = sin θ/cos θ = x/y
Q4.The pair of linear equations y = 0 and y =-5 has
(a) One solution (b) Two solutions (c) Infinitely many solutions (d) No solution
Ans.(d) No solution
y = 0 is equation of x-axis and the line y = -5 is parallel to x -axis
Q5.A fair die is thrown once. The probability of even composite number is
(a) 0 (b) 1/3 (c) 3/4 (d) 1
Ans.(b) 1/3
Total number of outcomes 1,2,3,4,5,6 (i.e 6)
The even composite numbers are 4,6 (i.e 2)
P( getting an even composite numbers) = no. of even composite nombers/total possible outcomes = 2/6 = 1/3
Q6.8 chairs and 5 tables cost Rs.10500, while 5 chairs and 3 tables cost Rs.6450. The cost of each chair will be
(a) Rs 750 (b) Rs 600 (c) Rs 850 (d) Rs 900
Ans. (a) Rs 750
Let the cost of one chair is Rs x and cost of one table is Rs y
According to first condition
8x + 5y = 10500…….(i)
According to second condiition
5x + 3y = 6450……..(ii)
Multiplying equation (i) by 3 and equation (ii) by 5,we get the equation (iii) and equation (iv)
24x +15y = 31500…..(iii)
25x + 15y =32250…….(iv)
Substracting equation (iv) from equation (iii)
-x = -750 ⇒ x = 750
Putting the value of x in equation (i)
8×750 + 5y = 10500
5y = 10500 – 6000 =4500
y = 900
Hence the cost of one chair is Rs 750 and the cost of a table is Rs 900
Q7.If cos θ+cos2θ =1,the value of sin2θ+sin4θ is
(a) -1 (b) 0 (c) 1 (d) 2
Ans.(c) 1
The given equation is cosθ+cos2θ =1
cos θ = 1 – cos²θ = sin²θ……(i)
Rewritting the given expression
sin2θ+sin4θ is= sin²θ + (sin²θ)²
Putting the value of sin²θ = cos θ from equation (i)
sin²θ + cos ²θ = 1
Q8. The decimal representation of 23/2³×5² will be
(a) Terminating (b) Non-terminating (c) Non -terminating and repeating (d) Non-terminating and non-repeating
Ans.(a) Terminating
If P and Q are prime numbers in the rational number P/Q then then its decimal expansion will be terminating if the prime factors of Q are in the form of 5n×2m
Q9. The LCM of 2³×3² and 2²× 3³ is
(a) 2³ (b) 3³ (c) 2³×3³ (d) 2²×3²
Ans.(c) 2³×3³
The given numbers are 2³×3² and 2²× 3³
2³×3³ is the least common multiple of both given numbers
The preboard 2 Maths question paper standard
Q10.The HCF of two numbers is 18 and their product is 12960. Their LCM will be
(a) 420 (b) 600 (c) 720 (d) 800
Ans.(c) 720
The HCF of two numbers is = 18 and the product of numbers is 12960
The relationship between HCF,LCM of the given numbers is as follows
LCM ×HCF = Product of numbers
LCM ×18 = 12960
LCM = 12960/18 =720
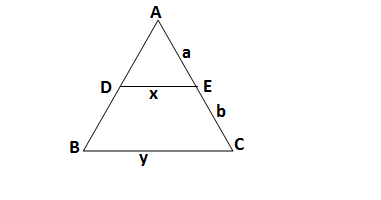
Q11.In the given figure, DE ∥ BC. Which of the following is true?
(a) (a +b)/xy (b) y = ax/(a +b) (c) x = ay/(a +b) (d) x/y = a/b
Ans. (c) x = ay/(a +b)
In fig. considering the ΔABC and ΔADE
∠A = ∠A (common)
∠ADE = ∠ABC (DE is parallel to BC and AB is the transversal,so both angles are corresponding angles)
∴ΔABC ∼ ΔADE (AA rule criteria of similar traingles)
Applying the theorem of similar triangles
DE/BC = AE/AC
x/y = a/(a +b)
x = ay/(a +b)
See the video for solutions of Maths(Basic) Term 1 preboard exam 2021
Q12.The co-ordinates of the point P dividing the line segment joining the points A (1,3) and B (4,6) internally in the ratio 2:1 are
(a) (2,4) (b) (4,6) (c) (4,2) (d) (3,5)
Ans. (d) (3,5)
Let the point P(x,y) divides the line segment A(1,3) and B(4,6) internally in the ratio 2 : 1
Applying section formula
x= (mx2 +nx1)/(m +n), y = (my2 +ny1)/(m +n)
Putting m =2 and n = 1,x2 =4,x1 =1,y1= 3 and y2= 6
x = (2×4 +1×1)/(2 +1), y = (2×6 +1×3)/(2 +1)
x =9/3, y =15/3
x = 3 and y = 5
Hence coordinates of P are (3,5)
Q13. The prime factorisation of 3825 is
(a) 3×52 ×21 (b) 32 ×52 ×35 (c) 32 ×52 × 17 (d) 32 ×25×17
Ans. (c) 3² × 5² × 17
3825 = 3²× 5² × 17
Q14.In the figure given below, AD=4cm,BD=3cm and CB=12 cm, then cot θ equals
(a) 3/4 (b) 5/12 (c) 4/3 (d) 12/5
Ans.(d) 12/5
In ΔABC ,∠B = 90°, ∠C = θ and ∠D = 90° in ΔABD
AD = 4 cm, BD = 3 cm, CB = 12 cm
cot θ = CB/AB
AB = √(BD² + AD²) = √(3²+4²) =√(9 +16) = √25 = 5 cm
cot θ = 12/5
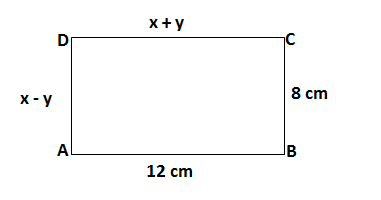
Q15.If ABCD is a rectangle , find the values of x and y
(a) x=10,y=2 (b) x=12,y=8 (c) x=2,y=10 (d) x=20,y=0
Ans. DC = AB = 12 cm (opposite sides of rectangle)
x + y = 12……(i)
AD = BC = 8 (opposite sides of rectangle)
x – y = 8 ……(ii)
From equation (i) and (ii)
2x = 20⇒ x = 10 and y =2
Q16.In an isosceles triangle ABC, if AC=BC and AB2=2AC2, then the measure of angle C will be
(a) 30˚ (b) 45˚ (c) 60˚ (d) 90˚
Ans.(d) 90°
In ΔABC, we are given AC = BC
AB² = 2AC²
AB² = AC² + AC²
AB² = AC² + BC²
Hypotenuse² = Base² + Perpendicular²
Terefore ΔABC is a right triangle in which ∠C = 90°
Q17.If -1 is a zero of the polynomial p(x)=x2 – 7x – 8 , then the other zero is
(a) -8 (b) -7 (c) 1 (d) 8
Ans. If – 1 is a zero of the polynomial p(x)=x2 – 7x – 8,then its one of the factor is (x +1)
Dividing x2 – 7x – 8 by (x +1)
Therefore (x – 8) is one of the factor of x² – 7x – 8
Q18.In a throw of a pair of dice, the probability of the same number on each die is
(a) 1/6 (b) 1/3 (c) 1/2 (d) 5/6
Ans. (a) 1/6
Total outcomes when a pair of dice is thrown are = 6²= 36
The outcomes showing the same digits in both dice are (1,1),(2,2),(3,3),(4,4),(5,5),(6,6) i.e 6
P( getting the number in both dice) = the outcomes showing the same number in both dice/total outcomes = 6/36 = 1/6
Q19.The mid-point of (3p,4) and (-2,2q) is (2,6) . Find the value of p+q
(a) 5 (b) 6 (c) 7 (d) 8
Ans. (b) 6
The given points are (3p,4) and (-2,2q)
The mid point of the line segment joining the given points is (2,6)
Therefore
(3p -2)/2, (4 +2q)/2 = 2,6
(3p -2)/2 = 2 and (4 +2q)/2 = 6
3p -2 = 4 and 4 + 2q = 12
3p = 6 and 2q = 8
p = 2 and q = 4
p + q = 2 + 4 = 6
Q20. The decimal expansion of 147/120 will terminate after how many places of decimals?
(a) 1 (b) 2 (c) 3 (d) 4
Ans.(c) 3
147/120 =(3 ×7²)/(2³×5×3) =49/(2³×5)
Hence the decimal expansion of the given number will terminate after 3 places.
SECTION B
Q21.The perimeter of a semicircular protractor whose radius is ‘r’ is
(a) π + 2r (b) π + r (c) πr (d) πr + 2r
Ans.(d) πr + 2r
The perimeter of the semicircular protractor whose radius is given ‘r’ = circumference +diameter =2πr/2 + 2r = πr + 2r
Q22.If P (E) denotes the probability of an event E, then
(a) 0< P(E) ≤ (b) 0 < P(E) < 1 (c) 0 ≤ P(E) ≤1 (d) 0 ≤P(E) <1
Ans. (c) 0 ≤ P(E) ≤1
The probability of an event that is hundred percent sure is 1 and which is impossible to occur is 0,so the probability of any event is greater and equal to 0 and less and equal to 1.
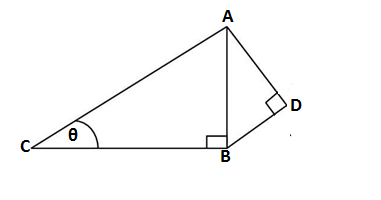
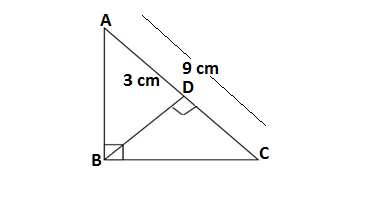
Q23.In ∆ABC, ˂B=90˚ and BD ⊥ AC. If AC = 9cm and AD = 3 cm then BD is equal to
(a) 2√2 cm (b) 3√2 cm (c) 2√3 cm (d) 3√3 cm
Ans. (b) 3√2 cm
In ΔABC, we are given ∠B = 90°, AC = 9 cm and AD = 3 cm
DC = 9 – 3 = 6 cm
We know, if ΔABC is a right triangle in which AB⊥BC and BD ⊥ AC
Then ΔABC∼ΔADB, ΔABC ∼ ΔBDC
So, ΔADB ∼ ΔBDC
Applying the theorem of similar triangle
AD/BD = BD/DC = AB/BC
∴BD² = AD.DC =3×6 = 18
BD =√18 = 3√2 cm
Q24.The pair of linear equations 3x+5y=3 and 6x+ky=8 do not have a solution if
(a) K=5 (b) K=10 (c) k≠10 (d) k≠5
Ans.(b) k = 10
Comparing the coefficients of the given pair of linear equations 3x+5y=3 and 6x+ky=8 with the standard pair of linear equations a1x +b1y+ c1 and a2x +b2y+ c2
a1 /a2 =3/6, b1 /b2 =5/k, c1 /c2 =-3/-8 = 3/8
The relationship between the coefficients is as follows when a pair of equation have no solutions
a1 /a2 = b1 /b2 ≠ c1 /c2
3/6 = 5/k ≠ 3/8
3/6 = 5/k and 5/k ≠ 3/8
k = 10 and k ≠ 40/3
Class 10 maths(Standard) preboard 2 Question paper solutions Term 1 2021-22
Q25.If the circumference of a circle increases from 2π to 4π then its area…………..the original area
(a) Half (b) Double (c) Three times (d) Four times
Ans.(d) Four times
The given circumference of the circles are 2π and 4π
Let the original radius of the circle r is increased to R
Circumference of the circle = 2πr
2πr = 2π⇒r = 1 unit and 2πR = 4π ⇒R = 2 unit
Area of original circle =πr² and area of modified circle =πR²
Area of original circle =π×1²=π and area of modified circle =π×2²=4π
area of modified circle/area of original circle = 4π/π =4
Area of modified circle = 4×Area of the original circle
Q26.Given that sin θ=a/b , then tan θ is equal to
(a) b/√(a² +b²) (b) b/√(b² -a²) (c) a/√(a² -b²) (d) a/√(b² -a²)
Ans.(d) a/√(b² -a²)
sin θ=a/b = perpendicular(p)/hypotenuse(h)
Therefore, base = √(h²- p²) = √(b²- a²)
tan θ =perpendicular(p)/ base(b)= a/√(b²- a²)
Q27.If x = 2sin2θ and y = 2cos2θ+1 then x+ y is
(a) 3 (b) 2 (c) 1 (d) 1/2
Ans.(a) 3
x +y
Putting the value of x =2sin2θ and y = 2cos2θ+1
2sin2θ + 2cos2θ+1
2(sin2θ + cos2θ) + 1
2 + 1 = 3 (since sin2θ + cos2θ=1)
Q28.If the difference between the circumference and the radius of a circle is 37cm ,π=22/7, the circumference (in cm) of the circle is
(a) 154 (b) 44 (c) 14 (d) 7
Ans. (b) 44 cm
Let the radius of the circle is = r
Circumference of the circle is = 2πr
According to question
2πr – r = 37
r(2π -1) = 37
r(2 ×22/7 – 1) = 37
r(44/7 – 1) = 37
(44 -7)r/7 = 37
37r = (7×37)
r = 7
Circumference = 2πr = 2×(22/7)×7 = 44 cm
Q29.The least number that is divisible by all the numbers from 1 to 10 (both inclusive)
(a) 100 (b) 1000 (c) 2520 (d) 5040
Ans. (c) 2520
The least number that is divisible by all the numbers from 1 to 10 is the LCM of all the numbers
LCM (1 to 10) =2×2×3×5×7×2×3 = 2520
Q30.Three bells ring at intervals of 4, 7 and 14 minutes. All three rang at 6 AM. When will they ring together again?
(a) 6:07 AM (b) 6:14 AM (c) 6:28 AM (d) 6:25 AM
Ans. We are given that three bells ring at intervals of 4, 7 and 14 minutes
Finding the LCM of 4,7 and 14
4 = 2²×1
7 = 7×1
14 = 7×2
LCM(4,7,14) = 2²×7 = 28
The bells will ring together after 28 minutes
If the bells ring together at 6 AM then they will ring together at 6 : 28 AM
Q31.What is the age of father, if the sum of the ages of a father and his son in years is 65 and twice the difference of their ages in years is 50?
(a) 40 years (b) 45 years (c) 55 years (d) 65 years
Ans.Let the age of father is x and of son is y
According to first condition
x + y = 65………(i)
According to second condition
2( x – y) = 50
x – y = 25…….(ii)
Adding both equations
2x = 90
x = 45
Putting the value of x in equation (i)
45 + y = 65
y = 65 – 45 = 20
Hence the age of father is 45 years and of son is 20 years
Q32.What is the value of (tan θ cosec θ)²-(sin θ sec θ)²
(a)-1 (b) 0 (c) 1 (d) 2
Ans.(c) 1
(tan θ cosec θ)²– (sin θ sec θ)²
Simplifying it
[(sin θ/cos θ)(1/sin θ)]² – (sin θ. 1/cos θ)²
(1/cos θ)² – (sin θ/cos θ)²
sec²θ – tan²θ = 1
Q33. The perimeters of two similar triangles are 26 cm and 39 cm.The ratio of their areas will be
(a) 2:3 (b) 6:9 (c) 4:6 (d) 4:9
Ans. (d) 4:9
Let two similar Δ’s are ΔABC ∼ DEF
Applying the rule of similar triangles
AB/DE = BC/EF = AC/DF
AB/DE = BC/EF = AC/DF = (AB + BC + AC)/(DE + EF + DF)
The relationship between the areas and sides of the triangle is
ar ΔABC/ar ΔDEF = (AB/DE)² = (BC/EF)² = (AC/DF)² = [(AB + BC + AC)/(DE + EF + DF)]²
We are given AB + BC + AC = 26 and DE + EF + DF = 39
ar ΔABC/ar ΔDEF = [(AB + BC + AC)/(DE + EF + DF)]²
ar ΔABC/ar ΔDEF = (26/39)² = (2/3)² = 4/9
Q34.There are 20 vehicles-cars and motorcycles in a parking area. If there are 56 wheels together, how many cars are there?
(a) 8 (b) 10 (c) 12 (d) 20
Ans. Let the number of cars are x and number of motorcycles are y in the park
Total vehicles in the park are 20
x + y = 20 …….(i)
The car has 4 wheels and motorcycle has 2 wheels
There are total 56 wheels
4x + 2y = 56
2x + y = 28…….(ii)
Substracting equation (ii) from equation (i)
– x = -8 ⇒ x = 8
Putting x = 8 in equation (i)
8 + y = 20 ⇒ y = 12
Hence the number of cars in the park are 8 and number of motor bikes are 12
Q35.A man goes 15m due west and then 8m due north. How far is he from the starting point?
(a) 7m (b) 10m (c) 17m (d) 23m
Ans. (c) 17m
The distance covered by the man towards the west is,AB= 15 km and towards north is,BC= 8 km
∴ AB ⊥ BC
ΔABC is the right triangle in which ∠B = 90° and AC is the hypotenuse(i.e distance from the starting point)
Applying pythogorus theorem
AC² = AB² + BC²
AC² = 15² + 8²= 225 +64 =289
AC =√289 = 17
Q36.What is the length of an altitude of an equilateral triangle of side 8cm?
(a) 2√3 cm (b) 3√3 cm (c) 4√3 cm (d) 5√3 cm
Ans. Let the equilateral triangle is ΔABC in which AD is the altitude
Since altitude of the equilateral triangle bisects the opposite sides drawn from a vertex
ΔABD is a right triangle in which ∠D =90° and AB is hypotenuse
AB² = AD² + BD²
8² = AD² + (BC/2)²
AD² = 8² – (BC/2)²
AB = BC = AC = 8 cm
AD² = 64 – (8/2)² = 64 – 16 = 48
AD = √48
AD = 4√3
Q37.If the letters of the word RAMANUJAN are put in a box and one letter is drawn at random. The probability that the letter is A is
(a) 3/5 (b) 1/2 (c) 3/7 (d) 1/3
Ans. (d) 1/3
The number of letters in RAMANUJAN are 9
The frequency of A in the given word is 3
Probability of drawing the letter A =The frequency of A in the given word/The number of letters in word = 3/9 = 1/3
Q38.Area of a sector of a circle is 1/6 to the area of circle. Find the degree measure of its minor arc.
(a) 90˚ (b) 60˚ (c) 45˚ (d) 30˚
Ans. (b) 60˚
Area of the circle is = πr² and area of sector = (θ/360°)πr²,where θ is degree measure of its minor arc
According to question
(θ/360°)πr² = (1/6) πr²
θ/360° = 1/6
θ = 360° /6 = 60°
Q39.A vertical stick 20m long casts a shadow 10m long on the ground. At the same time a tower casts a shadow 50m long. What is the height of the tower?
(a) 30m (b) 50m (c) 80m (d) 100m
Ans. (d) 100m
The object and its shadow are perpendicular to each other
Let the stick AB cast a shadow of the length BC and the tower DE cast a shadow of the length EF
ΔABC ∼ΔDEF
Applying the rule of similar triangles
AB/DE = BC/EF = AC/DF
AB = 20 cm, BC = 10 cm,EF = 50 m
20/DE = 10/50
10 DE = 50 ×20 = 1000
DE = 100
Height of tower is 100 m
Q40.What is the solution of the pair of linear equations 37x + 43y = 123,43x + 37y =117 ?
(a) x= 2,y= 1 (b) x= -1,y = 2 (c) x = -2,y = 1 (d) x = 1,y = 2
Ans.(d) x = 1,y = 2
The given pair of linear equations is 37x + 43y = 123…….(i) 43x + 37y =11……..(ii)
Substituting the value x = (123 – 43y)/37 in equation (ii)
43 (123 – 43y)/37 + 37y = 117
(5289 -1849y + 1369y)/37 = 4329
5289 – 480y = 4329
480 y = 5289 – 4329= 960
y = 960/480 = 2
Putting the value y = 2 in equation (i)
37x + 43×2 = 123
37x + 86 = 123
37x = 123 – 86 = 37
x = 1
SECTION C
Case study based questions
Section C consists of 10 questions of 1 mark each. Any 8 questions are to be attempted.
Case Study -1
Pacific Ring of Fire
The Pacific Ring of Fire is a major area in the basin of the Pacific Ocean where many earthquakes and volcanic eruptions occur. In a large horseshoe shape, it is associated with a nearly continuous series of oceanic trenches, volcanic arcs, and volcanic belts and plate movements.
Large faults within the Earth’s crust result from the action of plate tectonic forces, with the largest forming the boundaries between the plates. Energy release associated with rapid movement on active faults is the cause of most earthquakes.
Positions of some countries in the Pacific ring of fire is shown in the square grid above.
Based on the given information, answer the questions NO. 41-45
Q41.The distance between the point Country A and Country B is
(a) 4 units (b) 5 units (c) 6 units (d) 7 units
Ans.(b) 5 units
For getting the distance between the point country A(1,4) and country B (4,0) applying the distance formula
d = √[(4 -1)² +(0 -4)²] = √(3² +4²) = √(9 +16) = √25 = 5 units
Q42.Find a relation between x and y such that the point (x,y) is equidistant from the Country C and Country D
(a) x – y =2 (b) x +y = 2 (c) 2x – y = 0 (d) 2x + y = 2
Ans.(a) x – y =2
The coordinates of Country C are (7,1) and of Country D are (3,5)
The distance between C(7,1) and (x,y) = The distance between D(3,5) and (x,y)
√[(7-x)² +(1 -y)²] = √[(3-x)² +(5 -y)²]
49 +x² – 14x + 1 +y² – 2y = 9 +x² -6x + 25 +y² -10y
49 – 14x + 1 – 2y = 9 -6x + 25 -10y
– 14x + 6x – 2y +10y = 34 -49 -1 = -16
-8x + 8y = -16
x – y = 2
Q43.The fault line 3x + y – 9 = 0 divides the line joining the Country P(1, 3) and Country Q(2, 7) internally in the ratio
(a) 3 : 4 (b) 3 : 2 (c) 2 : 3 (d) 4 : 3
Ans. (a) 3 : 4
Let the line 3x + y – 9 = 0 divides the line joining the Country P(1, 3) and Country Q(2, 7) in the ratio of k : 1
Let the coordinates of the point of intersection of the given line and the line segment joining the points P(1, 3) and Country Q(2, 7)
x = (2k +1)/(k +1) and y = (7k +3)/(k +1)
Putting the values of x and y in the given equation
3(2k +1)/(k +1) + (7k +3)/(k +1) – 9 = 0
6k + 3 + 7k + 3 – 9k – 9 = 0
4k = 9 -3-3 = 3
k = 3/4
Q44.The distance of the Country M from the x-axis is
(a) 1 units (b) 2 units (c) 3 units (d) 5 units
Ans.(c) 3 units
The coordinates of Country M are (2,3)
Distance from x-axis is = y-coordinate = 3 units
Q45.What are the co-ordinates of the Country lying on the mid-point of Country A and Country D?
(a) (1, 3) (b) (2, 9/2) (c) (4, 5/2) (d) (9/2, 2)
Ans. (b) (2, 9/2)
The position of the country A is (1,4) and of Country D is (3,5)
The co-ordinates of the Country lying on the mid-point of Country A and Country D are =(1 +3)/2, (4 +5)/2 = (2,9/2)
Case Study -2
ROLLER COASTER POLYNOMIALS
Polynomials are everywhere. They play a key role in the study of algebra, in analysis and on the whole many mathematical problems involving them.Since, polynomials are used to describe curves of various types engineers use polynomials to graph the curves of roller coasters.
Based on the given information, answer the questions NO. 46-50.
Q46.If the Roller Coaster is represented by the following graph y=p(x) , then name the type of the polynomial it traces.
(a) Linear (b) Quadratic (c) Cubic (d) Bi-quadratic
Ans. (c) Cubic
The polynomial y=p(x), is intersecting the x-axis in three points,so it has three zeroes that signifies it is a polynomial of degree three or cubic polynomial.
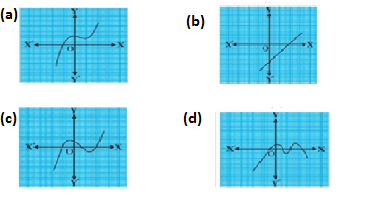
Q47.The Roller Coasters are represented by the following graphs y=p(x). Which Roller Coaster has more than three distinct zeroes?
Ans.(d)
The polynomial y=p(x), is intersecting the x-axis at more than three points, it has four zeroes
Q48.If the Roller Coaster is represented by the cubic polynomial t(x)= px3+qx2+rx+s , then which of the following is always true
(a) s≠0 (b) r≠0 (c) q≠0 (d) p≠0
Ans. (d) p≠0
The cubic polynomial is a polynomial of degree 3,if p =0 in the given polynomial then it will become qx² +rx +s,so p must be non-zero in t(x)= px3+qx2+rx+s
Q49.
If the path traced by the Roller Coaster is represented by the above graph y=p(x), find the number of zeroes?
(a) 0 (b) 1 (c) 2 (d) 3
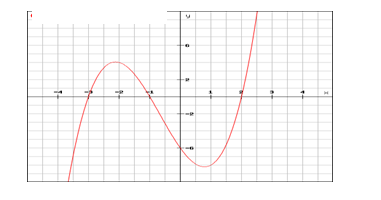
Ans. (d) 3
Q50.
If the path traced by the Roller Coaster is represented by the above graph y=p(x), find its zeroes?
(a) -3, -6, -1 (b) 2, -6, -1 (c) -3, -1, 2 (d) 3, 1, -2
Ans. (c) -3, -1, 2
The polynomial y=p(x), is intersecting the x-axis in three points at x = -3, -1 and 2
You can compensate us by donating any amount of money for our survival
Our Paytm No 9891436286
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions of class 9 maths
| Chapter 1- Number System | Chapter 9-Areas of parallelogram and triangles |
| Chapter 2-Polynomial | Chapter 10-Circles |
| Chapter 3- Coordinate Geometry | Chapter 11-Construction |
| Chapter 4- Linear equations in two variables | Chapter 12-Heron’s Formula |
| Chapter 5- Introduction to Euclid’s Geometry | Chapter 13-Surface Areas and Volumes |
| Chapter 6-Lines and Angles | Chapter 14-Statistics |
| Chapter 7-Triangles | Chapter 15-Probability |
| Chapter 8- Quadrilateral |
NCERT Solutions of class 9 science
CBSE Class 9-Question paper of science 2020 with solutions
CBSE Class 9-Sample paper of science
CBSE Class 9-Unsolved question paper of science 2019
NCERT Solutions of class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT solutions of class 10 science
Solutions of class 10 last years Science question papers
CBSE Class 10 – Question paper of science 2020 with solutions
CBSE class 10 -Latest sample paper of science
NCERT solutions of class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions of class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
