Class 10 CBSE Maths Solutions of Important Questions of 6 th chapter -Triangle
Class 10 Maths Solutions of Important Questions of 6 th chapter -Triangle will help you to get the idea of solving the questions of the chapter 6 Triangle on your Maths question paper of Class 10 CBSE board exam .Study of Solutions of important questions of the class 10 chapter 6 contains selected questions of the chapter 6 triangle which has been asked in the previous year’s question papers of CBSE board exam . All questions are solved by an expert of maths who has 25 years of experience in teaching maths from 9 to 12 classes.
See the video-Solutions for class 10 maths exercise 6.1 Triangle
Class 10 Maths Solutions of Important Questions of 6 th chapter -Triangle
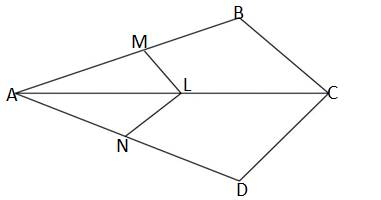
Q1. In the given figure ,if LM ∥ CB and LN ∥ CD.Prove that
Ans.
GIVEN: In the figure LM ∥ CB and LN ∥ CD
TO PROVE:
PROOF : In ΔABC ,we have
LM ∥ CB (given)
In ΔADC ,we have
LN ∥ CD (given)
From equation (i) and equation (ii)
Adding 1 both sides,we have
Hence,proved
Q2. In the given figure DE ∥ OQ and DF ∥ OR. Show that EF ∥ QR.
GIVEN:DE ∥ OQ and DF ∥ OR
TO PROVE EF ∥ QR.
PROOF: In ΔPOQ
DE ∥ OQ (given)
In ΔPOR
DF ∥ OR (given)
From equation (i) and equation (ii),we have
EF ∥ QR(converse of BPT theorem),Hence proved
See the video-Class 10 Maths NCERT Solurions Exercise 6.2 chapter 6 Triangles
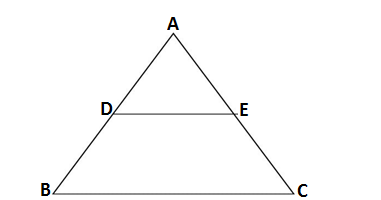
Q3. Using BPT ,prove that a line drawn through the mid point of one side of a triangle parallel to another side bisects the third side .(Recall that you have proved it in class IX).
Ans.
GIVEN: ΔABC in which DE ∥ BC
TO PROVE: DE bisects the sides AC
PROOF: In ΔABC
DE ∥ BC (given)
Since D is the mid point of AB
∴ AD = BD
Putting the value of AD in above equation
AE = CE
Therefore DE bisects AC, Hence proved
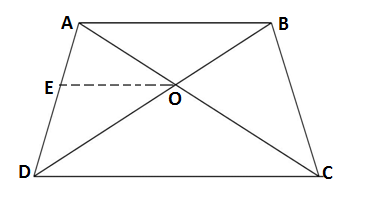
Q4.ABCD is a trapizium in which AB ∥ DC and its diagonals intersects each other at the point O. Show that
Ans.
GIVEN: Trapezium ABCD in which diagonal AC and BD bisect each other at O in which AB ∥ DC
TO PROVE:
CONSTRUCTION: Drawing OE ∥ AB ∥ DC
PROOF: In ΔABD
OE ∥ AB (constructed)
In ΔADC
OE ∥ DC (constructed)
From equation (i) and equation (ii)
Hence proved
Q5.The diagonal of a quadrilateral ABCD intersect each other at the point O such that
Show that ABCD is a trapizium
Ans.
GIVEN: The quadrilateral ABCD in which diagonal AC and BD intersect each other at the point O such that
TO PROVE: ABCD is a trapizium
CONSTRUCTION: Drawing EF ∥ DC
PROOF: In ΔADC
EF ∥ DC (constructed)
∴OE ∥ DC
From equation (i) and equation (ii)
∴OE ∥ AB (converse of BPT)
We also have OE ∥ DC
∴AB ∥ DC
Hence ABCD is a trapizium
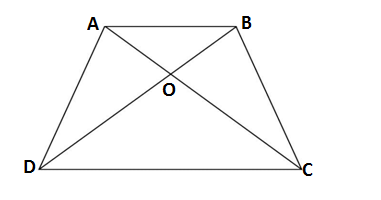
Q6.Diagonals AC and BD of a trapezium ABCD with AB ∥ DC intersect each other at the point O. Using a similarity criterion for two triangles, show that
Ans.
GIVEN: Trapezium ABCD with AB ∥ DC in which diagonal AC and BD bisect each other at O
TO PROVE:
PROOF : In ΔAOB and ΔCOD
AB ∥ DC (given) and AC and BD are transversal
∴ ∠BAO = ∠OCD (alternate angle)
∴∠ABO = ∠ODC (alternate angle)
ΔAOB ∼ ΔCOD (AA similarity)
Applying the rule of similar triangles
Hence Proved
Q7.In the given figure and ∠1 = ∠2, show that ΔPQR ∼ ΔTQR.
Ans.
GIVEN: ∠1 = ∠2
TO PROVE:ΔPQR ∼ ΔTQR
PROOF: In ΔPQR and ΔTQR
∠1 = ∠2 (given)
PQ = PR
Substituting the value of PR =PQ in the given equation
∠1 = ∠1 (common)
ΔPQR ∼ ΔTQR (SAS criteria of similar triangle)
Q8.D is a point on the side BC of a triangle ABC, such that ∠ADC = ∠BAC. Show that CA² = CB.CD.
Ans.
GIVEN: ΔABC and D is a point on AC
Such that ∠ADC = ∠BAC
TO PROVE: CA² = CB.CD
PROOF: In ΔABC and ΔADC
∠DAC = ∠ABC
∠BAC = ∠ADC
ΔABC∼ ΔDAC (AA criteria of the similar triangle)
According to the rule of similar triangle
CA² = CB.CD, Hence proved
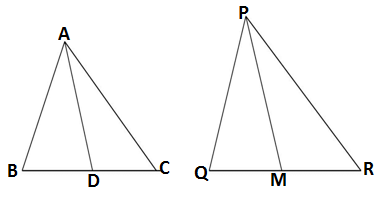
Q9.Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ∆PQR (see in given figure). Show that ∆ABC ~ ∆PQR.
Ans.
GIVEN: ΔABC and ΔPQR in which AD and PM are the medians of the triangles
TO PROVE:∆ABC ~ ∆PQR
PROOF: In ΔABC and ΔPQR
BD = CD = BC/2 (AD is the median of the triangle ABC)
QM = MR = QR/2 (PM is the median of the triangle PQR)
Rewriting the given relationship of the sides
ΔABD ∼ ΔPQM (SSS rule)
∠B = ∠Q ( corresponding angles of similar triangles)
∴∆ABC ~ ∆PQR ( SAS rule criteria of similar triangles)
Q10.Let ∆ABC ~ ∆DEF and their areas be, respectively, 64 cm² and 121 cm². If EF = 15.4 cm, find BC.
Ans. We are given that
∆ABC ~ ∆DEF and ar ∆ABC = 64 cm² , ar ∆DEF =121 cm²
Since ∆ABC ~ ∆DEF, therefore
It is given to us that EF = 15.4 cm
BC = √(125.44)= 11.2
Hence the value of BC is 11.2 cm
Q11.A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Ans. We are given the height of the vertical pole is = 6 m , Let height of the tower is h, the length of its shadow given to us is 28 m
In ΔABC and ΔPQR
∠B = ∠Q ( each of 90°)
∠C = ∠R (son’s altitude is same)
ΔABC∼ ΔPQR (AA rule )
According to the rule of similar triangle
4h = 168
h = 42
Hence the height of the tower is 42 m
You can compensate us by donating any amount of money for our survival
Other study inputs for Linear Equations in two variables and Pair of linear equations in two variables.
Class 10 maths NCERT solutions chapter 6-Triangles
Class 10 maths NCERT solutions of important questions of chapter 3 Pair of Linear Equations
NCERT Solutions of class 9 maths exercise 4.3 of chapter 4- Linear equations in two variables
How to creat and solve algebraic equations like linear and quadratic equations
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions of class 9 maths
| Chapter 1- Number System | Chapter 9-Areas of parallelogram and triangles |
| Chapter 2-Polynomial | Chapter 10-Circles |
| Chapter 3- Coordinate Geometry | Chapter 11-Construction |
| Chapter 4- Linear equations in two variables | Chapter 12-Heron’s Formula |
| Chapter 5- Introduction to Euclid’s Geometry | Chapter 13-Surface Areas and Volumes |
| Chapter 6-Lines and Angles | Chapter 14-Statistics |
| Chapter 7-Triangles | Chapter 15-Probability |
| Chapter 8- Quadrilateral |
NCERT Solutions of class 9 science
CBSE Class 9-Question paper of science 2020 with solutions
CBSE Class 9-Sample paper of science
CBSE Class 9-Unsolved question paper of science 2019
NCERT Solutions of class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT solutions of class 10 science
Solutions of class 10 last years Science question papers
CBSE Class 10 – Question paper of science 2020 with solutions
CBSE class 10 -Latest sample paper of science
NCERT solutions of class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions of class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |