Class 10 Solutions of Maths (Basic) Question Paper Term 1 CBSE Board 2021-22
Class 10 Solutions of Maths (Basic) Question Paper Term 1 CBSE Board 2021-22 created here for helping class 10 students who has basic maths in clearing their doubts . They can check their answers and see the solutions for the clearance of doubts ,it is mandatory for all students to go through the solutions of class 10 Maths (Basic) Question Paper Term 1 CBSE Board 2021-22 because in term 2 CBSE Board 2021-22 they have to tackle with 50 percent descriptive questions of total questions.
Class 10 Maths(Standard) Solutions of Question Paper Set 4 Term 1 CBSE Board Exam 2021-22

Class 10 Solutions of Maths (Basic) Question Paper Term 1 CBSE Board 2021-22
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
Q1. HCF of 92 and 152 is
(a) 4 (b) 19 (c) 23 (d) 57
Ans. 92 =2²×23
152 = 2³× 19
HCF (92,152) = 2²= 4
Q2. In ΔABC , DE ∥ BC, AD =4 cm,DB =6 cm and AE =5cm. The length of EC is
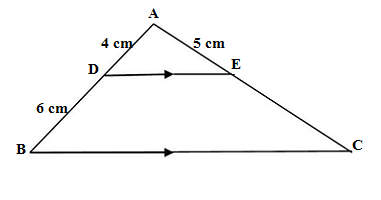
(a) 7 cm (b)6.5 cm (c) 7.5 cm (d) 8 cm
Ans. (c) 7.5 cm
In ΔABC , DE ∥ BC
Applying BPT theorem
AD/BD = AE/EC
4/6 = 5/EC
4EC = 30
EC = 30/4 = 7.5 cm
Q3. The value of k, for which the pair of linear equations x + y – 4 = 0, 2x + ky -3 =0 have no solution,is
(a) 0 (a) 2 (a) 6 (a) 8
Ans: (a) 2
A pair of linear equations a1x +b1y +c1 and a2x +b2y +c2 are parallel when
a1/a2 = b1/b2≠c1/c2
In equations x +y -4=0 and 2x + ky – 3=0
1/2 =1/k≠-4/-3
k = 2
Q4. The value of (tan²45° – cos²60° ) is
(a) 1/2 (b) 1/4 (c) 3/2 (d) 3/4
Ans. (d) 3/4
tan²45° – cos²60° = 1² – (1/2)² = 1 -1/4 = 3/4
Q5.A point (x,1) is equidistant from (0,0) and (2,0). The value of x is
(a)1 (b)0 (c) 2 (d) 1/2
Ans.Let the point A(x,1), B (0,0) and C (2,0)
According to question
AB = AC
√[(x-0)²+(1-0)²] = √[(x-2)²+(1-0)²]
x² +1 = x² +4 -4x +1
-4x +5 = 1
-4x = -4
x = 1
Q6.Two coins are tossed together .The probability of getting exactly one head is
(a)1/4 (b)1/2 (c) 3/4 (d) 1
Ans. (b)1/2
When two coins are tossed together then total outcomes are (HH),(TT),(HT),(TH)
The outcomes with exacty one head are (HT),(TH)
P(getting exactly one head) =2/4 = 1/2
Q7.A circular arc of length 22 cm subtends an angle θ at the centre of the circle of radius 21 cm. The value of θ is
(a)90° (b)50° (c) 60° (d) 30°
Ans.(c) 60°
Length,l of the arc is given by
l = 22 cm, r = 21 cm
Q8.A quadratic polynomial having sum and product of its zeroes as 5 and 0 respectively, is
(a)x2+5x (b)2x(x -5) (c) 5x2-1 (d) x2-5x+5
Ans.(b)2x(x -5)
The quadratic equation is given as
k(x² -(sum of the zeroes)x +product of the zeroes)
(kx² – 5x) =kx(x -5)
The answer is 2x(x -5) where k=2
Q9.If P(E) = 0.65, then the value of P(not E) is
(a)1.65 (b)0.25 (c) 0.65 (d) 0.35
Ans.(d) 0.35
We know
P(E) + P(not E) =1
P(not E) = 1 – P(E) = 1 – 0.65 = 0.35
Q10.It is given that ∆DEF ∼ ∆PQR . EF : QR =3: 2,then value of ar(DEF) : ar(PQR) is
(a)4 :9 (b)4:3 (c) 9:2 (d) 9:4
Ans.It is given to us that
∆DEF ∼ ∆PQR in which EF : QR =3: 2
Since ratio between areas of two triangle is equal to the ratios between the square of their corresponding sides
ar(DEF)/ar(PQR) = (EF /QR)² =(3/2)² =9/4
Q11.Zeroes of a quadratic polynomial x2-5x +6 are
(a)-5,1 (b)5,1 (c)2,3 (d)-2,-3
Ans.(c)2,3
The given quadratic polynomial is
x2-5x +6
Factorizing it
x2-3x-2x +6
x(x -3) -2(x – 3)
(x -3)(x -2)
x =3,x =2
Q12.57/300 is a
(a)non-terminating and non –repeating decimal expansion.
(b)terminating decimal expansion after 2 places of decimal.
(c)terminating decimal expansion after 3 places of decimal.
(a)non-terminating but repeated decimal expansion
Ans.(b)terminating decimal expansion after 2 places of decimal
57/300 = 19/100 = 19/10²
Therefore 10² at denominator shows that it is a terminating decimal expansion after 2 places of decimal.
Q13. Perimeter of rectangle whose length (l) is 4 cm more than twice its breadth (b) is 14 cm.The pair of linear equations representing the above information is
(a) l +4 =2b, 2(l+b) =14 (b) l -b=4, 2(l+b) =14 (c) l =2b+4, l+b =14 (d) l =2b+4, 2(l+b) =14
Ans. (d) l =2b+4, 2(l+b) =14
Length of rectangle is l and breadth of rectangle is b
According to first condition
2(l+b) =14
According to second condition
l= 2b +4
can also be written as
(a) 5.213213213…. (b) 5.2131313…. (c) 5.213 (d) 5253/1000
Ans. (a) 5.213213213….
is a recurrent infinite decimal, the sign of bar on 213 shows that 213 will repeat infinitely.
Q15. The ratio in which the point (4,0) divides the line segment joining the points (4,6) and (4,-8) is
(a) 1 : 2 (a) 3 : 4 (a) 4 : 3 (a) 1 : 1
Ans. (a) 3 : 4
Applying the section formula
-8k + 6 = 0
k = -6/-8 = 3/4
Q16. Which of the following is not defined ?
(a) sec 0° (b) cosec 90° (c) tan 90° (d) cot 90°
Ans. (c) tan 90°
tan 90° =sin 90° /cos 90° =1/0 = not defined
Q17. In the given figure ,a circle is touching a semi-circle at C and its diameter AB at O . If AB = 28 cm ,what is the radius of the inner circle ?
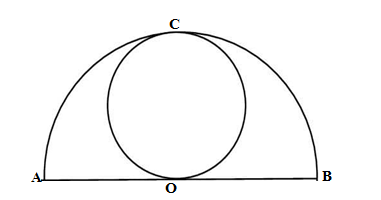
(a) 14 cm (b) 28 cm (c) 7 cm (d) 7/2 cm
Ans. (c) 7 cm
The given semicircle is OACB with diameter AB at O
From the figure OC is the diameter of the inner circle
OC = OB = AB/2 = 28/2 = 14 cm (radii of the semicircle)
Hence radius of inner circle is = OC/2 =14/2 =7 cm
Q18. The vertices of a triangle OAB are O(0,0), A(4,0) and B(0,6). The median AD is drawn on OB .The length AD is
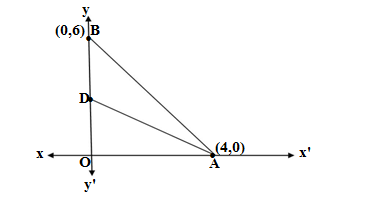
(a) √52 (b) 5 units (c) 25 units (d) 10 units
Ans. (b) 5 units
The given vertices of the triangle OAB are O(0,0), A(4,0) and B(0,6)
The point D is the midpoint of OB [since AD is the midian drawn from A on OB]
The coordinates of D are [(0+0)/2,(0+6)/2] =(0,3)
AD = distance between A(4,0) and D(0,3)
AD =√[(4-0)² +(0-3)²] =√[(4² +3²] =√[(16 +9] =√25 =5 units
Q19. In a right -angled triangle PQR , ∠Q = 90°. If ∠P = 45°,then value of tan P – cos²R is
(a) 0 (a) 1 (a) 1/2 (a) 3/2
Ans.(a) 0
In a right -angled triangle PQR , the given angles are ∠Q = 90°. If ∠P = 45°
∠R = 180° -(90°+45°) = 180°- 135° =45°
tan P – cos²R = tan 45° – cos²45° =1 -1²= 1-1 =0
Q20.If tan θ = 2/3, then the value of sec θ is
(a) √13/3 (b) √5/3 (c) √(13/3 ) (d) 3/√13
Ans.(a) √13/3
Given to us tan θ = 2/3
tan θ = p/b=2/3
h =√(p² +b²) = √(2² +3²) = √(4 +9) = √13
sec θ = h/b = √13/3
SECTION -B
Q21.The parimeter of the sector of a circle of radius 14 cm and central angle 45° is
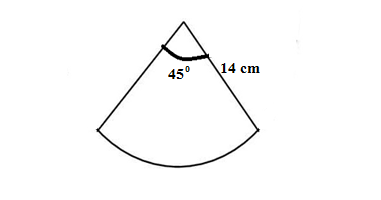
(a) 11 cm (b) 22 cm (c) 28 cm (d) 39 cm
Ans. (d) 39 cm
The perimeter of the sector is = radius(14 cm) ×2 + length of arc(l)
Perimeter of the sector is =14 ×2 +11 =28 +11 =39 cm
Q22. A bag contains 16 red balls , 8 green balls and 6 blue balls. One ball is drawn at random .The probability that it is blue ball is
(a) 1/6 (b) 1/5 (c) 1/30 (d) 5/6
Ans. Total number of balls =16 red balls+ 8 green balls + 6 blue ball =30 balls
The number of blue balls = 6 balls
P(getting a blue balls) = The number of blue balls/ Total number of balls =6/30 = 1/5
Q23. If sin θ – cos θ =0, then the value of θ is
(a) 30 ° (b) 45 ° (c) 90 ° (d) 0 °
Ans.(b) 45 °
The given equation is
sin θ – cos θ =0
sin θ = cos θ = sin (90° -θ)
θ = 90° -θ⇒ 2θ = 90°⇒θ =45°
Q24. The probability of happening of an event is 0.02. The probability of not happening of the event is
(a) 0.02 (b) 0.80 (c) 0.98 (d) 49/100
Ans. (c) 0.98
Let the probability of an event is P(E) and of not happening is P(not E)
We know
P(E) + P(not E) =1
P(E) =0.02 is given to us
0.02 + P(not E) =1
P(not E) = 1 – 0.02 = 0.98
Q25. Two concentric circles are centred at O. The area of shaded region ,if outer and inner radii are 14 cm and 7 cm respectively,is
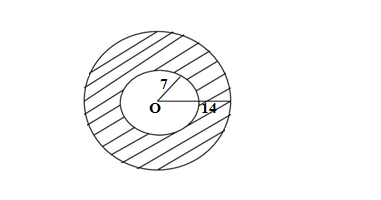
(a) 462 cm² (b) 154 cm² (c) 231 cm² (d) 308 cm²
Ans.(a) 462 cm²
The given concentric circles have outer and inner radii 14 cm and 7 cm repectively
The area of shaded region = Area of the outer circle – Area of inner circle
Area of circle =πr²
The area of outer circle =(22/7)×14×14 = 22 ×28 =616 cm²
The area of inner circle =(22/7)×7×7= 22 ×7 =154 cm²
∴ The area of shaded region = 616 -154 = 462 cm²
Q26. 1/(1+sin θ) + 1/(1-sin θ) can be simplified to get
(a) 2 cos²θ (b) (1/2) sec²θ (c) 2/sec²θ (d) 2sec²θ
Ans. The given expression is
1/(1+sin θ) + 1/(1-sin θ)
(1- sin θ +1+sin θ)/(1- sin θ) (1+sin θ) =2/(1-sin²θ) =2/cos²θ
Q27. The origin divides the line segment AB joining the points A(1,-3) and B(-3,9) in the ratio :
(a) 3 : 1 (b) 1 : 3 (c) 2 : 3 (d) 1 : 1
Ans. (b) 1 : 3
The given line segment AB joining the points A(1,-3) and B(-3,9)
Also given that origin(0,0) divides the line segment AB
Applying the section formula
0 =(-3k +1)/(k+1)(where k is the ratio by which the origin divides the line segment AB)
-3k +1⇒ k =1/3 ⇒1 :3
Q28.The perpendicular bisector of a line segment A(-8,0) and B(8,0) passes through a point (0,k). The value of k is
(a) 0 only (b) 0 or 8 only (c) any real number (d) any non-zero real number
Ans. (c) any real number
It is given that the perpendicular bisector of a line segment A(-8,0) and B(8,0) passes through a point (0,k)
The point (0,k) is equidistant from A(-8,0) and B(8,0)
√[(0+8)² +(k-0)²] =√[(0-8)² +(k-0)²]
√[64+k²] =√[64+k²]
It is possible for any real value of k
Q29.Which of the following is a correct statement?
(a) Two congruent figures are always similar
(b) Two similar figures are always congruent
(c) All rectangles are similar
(d) The polygons having the same number of sides are similar
Ans.(a) Two congruent figures are always similar
Two congruent figures like an example of a pair of equilateral triangles,a pair of square
All rectangles can not be similar because squares are also a special case of the rectangle which can’t be similar to other normal rectangles
Q30.The solutions of the pair of linear equations x =-5 and y =6 is
(a) (-5,6) (b) (-5,0) (c) (0,6) (d) (0,0)
Ans.(a) (-5,6)
The given pair of linear equations is
x =-5 and y =6
The line x=-5 passes through (-5,0) and the line y=6 passes through 6 (0,6)
Both of the lines x=-5 and y=6 intersects at (-5,6)
Therefore solutions of the pair of linear equations x =-5 and y =6 is (-5,6)
Q31.A circle of radius 3 units is centred at (0,0). Which of the following points lie outside the circle ?
(a) (-1,-1) (b) (0,3) (c) (1,2) (d) (3,1)
Ans. (d) (3,1)
The distance from (0,0) and (3,1) is = √[(3-0)²+(1-0)²]=√(9+1) =√10 units
Radius of circle is 3 units
Since √10 > 3
∴ The point (3,1) lies outside the circle
Q32.The value of k for which the pair of linear equations 3x +5y =8 and kx +15y =24 has infinitely many solutions ,is
(a) 3 (b) 9 (c) 5 (d) 15
Ans.(b) 9
The pair of linear equations 3x +5y =8 and kx +15y =24 has infinitely many solutions when
3/k = 5/15 =-8/-24
3/k = 5/15 ⇒ k=9
3/k=-8/-24 ⇒k=9,confirmed
Q33.HCF of two consecutive even numbers is
(a) 0 (b) 1 (c)2 (d) 4
Ans.(c)2
As an example two consecutive even numbers are 2 and 4
2 → 2 ×1
4→ 2² ×1
HCF(2,4) =2
Q34. The zeroes of quadratic polynomial x² +99x +127 are
(a) both negative
(b) both positive
(c) both positive or both negative
(d) reciprocal of each other
Ans.(b) both positive
The given quadratic polynomial is x² +99x +127
x² +99x +127
On comparing the coefficients with ax² +bx +c
Since a,b and c are positives,so both roots are positives
Q35.The mid -point of the line segment joining the points (-3,9) and (-6,-4) is
(a) (-3/2,-13/2) (b) (9/2,-5/2) (c) (-9/2,5/2) (d) (9/2,5/2)
Ans. (c) (-9/2,5/2)
The mid -point of the line segment joining the points (-3,9) and (-6,-4) is=[(-3-6)/2,(9-4)/2]=(-9/2,5/2]
Q36.The decimal expansion of 13/(2×5²×7) is
(a) terminating after 1 decimal place.
(b) non-terminating and non-repeating.
(c) terminating after 2 decimal places.
(d) non-terminating but repeating.
Ans.(d) non-terminating but repeating.
The given expression is
13/(2×5²×7)
The prime factors of the denominator are not of the form 2n×5nj,so its expansion is non-terminating but repeating
Q37.In ΔABC, DE ∥ BC, AD =2 cm, DB =3 cm, DE : BC is equal to

(a) 2 :3 (b)2 :5 (c)1 :2 (d)3 :5
Ans.(b)2 :5
It is given that In ΔABC, DE ∥ BC
∴ ∠ADE = ∠ABC (corresponding angle)
∠AED = ∠ACB (corresponding angle)
ΔABC ∼ΔADE (AA rule)
Therefore
AB/AD =BC/DE =AC/AE
(2+3)/2 =BC/DE
BC/DE = 5/2
DE/BC = 2/5
Q38.The (HCF ×LCM) for the numbers 50 and 20 is
(a) 1000 (b) 50 (c)100 (d) 500
Ans.(a) 1000
The given numbers are 50 and 20
We know
HCF ×LCM= Product of numbers=50×20 =1000
Q39.For which natural number n,6n ends with digit zero ?
(a) 6 (b) 5 (c)0 (d) None
Ans.(d) None
factorizing the given term is 6n =(2×3)n=2n×3n
The factor of the given number 6n are not in the form of 2m×5n ,therefore 6n will never end with digit zero
Q40.(1 +tan²A)(1 + sin A)(1 – sin A) is equal to
(a) cos²A/sec²A (b) 1 (c) 0 (d) 2
Ans.(b) 1
The given expression is
(1 +tan²A)(1 + sin A)(1 – sin A)
=sec²A(1-sin²A)
=sec²A.cos²A
= sec²A.1/sec²A = 1
Case Study-I
Sukriti throws a ball upwards, from a rooftop which is 8 m high from ground level. The ball reaches to some maximum height and then returns and hit the ground.
If the height of the ball at time t(in sec) is represented by h(m), then equation of its path is given as h = -t² +2t +8
Based on the above information, answer the following :
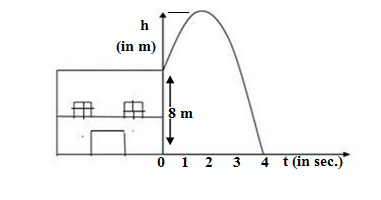
Q41.The maximum height achieved by ball is
(a) 7 m (b) 8 m (c) 9 m (d) 10 m
Ans. (b) 8 m
The maximum height is achieved at t=2 sec.
The polynomial is given as
h = -t² +2t +8
h(max.) =-2² +2×2 +8 =-4 +4+8 =8 m
Q42. The polynomial represented by above graph is
(a) linear polynomial (b) quadratic polynomial (c)constant polynomial (d) cubic polynomial
Ans. (b) quadratic polynomial
The power of polynomial is determined from the term (-t²),the highest power of the variable in the polynomial ,h = -t² +2t +8
Quadratic mean the power of 2
Q43. Time taken by ball to reach maximum height is
(a) 2 sec. (b) 4 sec. (c) 1 sec. (d) 2 min.
Ans. (a) 2 sec.
Q44.Number of zeroes of the polynomial whose graph is given is
(a) 1 (b)2 (c) 0 (d) 3
Ans. (b)2
Since given polynomial, ,h = -t² +2t +8 is a quadratic polynomial, therefore it has two zeroes
Q45. Zeroes of the polynomial are
(a) 4 (b)-2 ,4 (c)2,4 (d) 0,4
Ans.(b)-2 ,4
The given polynomial is
h = -t² +2t +8
-t² +2t +8 =0
t² -2t -8 =0
t² -4t +2t-8 =0
t(t-4) +2(t -4) =0
(t-4)(t+2)=0
t=4 and t=-2
Case Study -II

Quilts are available in various colours and designs .Geometrical designs includes shapes like squares ,triangles,rectangles,haxagones etc.
One such designs is shown above .Two triangles are heighlighted ,ΔPQR.
Based on above information ,answer the following questions:
Q46.Which of the following criteria is not available for ΔABC to be similar to ΔQRP ?
(a) SAS (b) AAA (c) SSS (d) RHS
Ans.(a) SAS
In ΔABC and ΔQRP
AB =AC=x, QR =x +x =2x and QP=x +x =2x
AB/QR =AC/QP =x/2x=1/2
∠BAC =∠PQR =90°(angles of square)
ΔABC∼ ΔQRP(SAS rule)
Q47.If each square is of length x units ,then length BC is equal to
(a) x√2 unit (b) 2x unit (c) 2√x unit (d) x√x unit
Ans.(a) x√2 unit
Applying Pythagoras theorem
BC =√(AB² +AC²) =√(x² +x²)=√2x²=x√2 unit
Q48. Ratio BC : PR is equal to
(a) 2 : 1 (b) 1 : 4 (c) 1 : 2 (d) 4 : 1
Ans. (c) 1 : 2
BC =x√2 unit and PR =2BC=2x√2 unit
BC : PR = x√2 : 2x√2 = √2 : 2√2 = 1 :2
Q49.ar(PQR) : ar(ABC) is equal to
(a) 2 : 1 (b) 1 : 4 (c) 4 : 1 (d) 1 : 8
Ans. (c) 4 : 1
Since ΔPQR∼ΔABC
∴ar(PQR) : ar(ABC) =PQ²/AB²=(2x)²/x²= 4x²/x² =4/1
Q50.Which of the following is not true ?
(a) ΔTQS ∼ ΔPQR (b) ΔCBA ∼ ΔSTQ (c) ΔBAC ∼ ΔPQR (d) ΔPQR ∼ ΔABC
Ans.(d) ΔPQR ∼ ΔABC
Since ∠P ≠∠A, ∠Q ≠∠B
∴ΔPQR ∼ ΔABC but it should be rewritten as ΔPQR ∼ ΔBAC
You can compensate us by donating any amount of money for our survival
Our Paytm No 9891436286
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions of class 9 maths
| Chapter 1- Number System | Chapter 9-Areas of parallelogram and triangles |
| Chapter 2-Polynomial | Chapter 10-Circles |
| Chapter 3- Coordinate Geometry | Chapter 11-Construction |
| Chapter 4- Linear equations in two variables | Chapter 12-Heron’s Formula |
| Chapter 5- Introduction to Euclid’s Geometry | Chapter 13-Surface Areas and Volumes |
| Chapter 6-Lines and Angles | Chapter 14-Statistics |
| Chapter 7-Triangles | Chapter 15-Probability |
| Chapter 8- Quadrilateral |
NCERT Solutions of class 9 science
CBSE Class 9-Question paper of science 2020 with solutions
CBSE Class 9-Sample paper of science
CBSE Class 9-Unsolved question paper of science 2019
NCERT Solutions of class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT solutions of class 10 science
Solutions of class 10 last years Science question papers
CBSE Class 10 – Question paper of science 2020 with solutions
CBSE class 10 -Latest sample paper of science
NCERT solutions of class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions of class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |



