NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry
NCERT Solutions for Class 10 Maths Exercise 8.1 of Chapter 8 Introduction to Trigonometry are created here for your help in boosting your preparation of the class 10 maths CBSE board exam. All questions of class 10 NCERT maths exercise 8.1 Introduction to Trigonometry are solved by a step-by-step method so every student of class 10 can understand the solutions with the clearance of doubts. Here you can study NCERT solutions of other chapters also. These NCERT Solutions class 10 maths exercise 8.1 will clear all your doubts about basic Trigonometry which is required to solve the questions of higher class maths.
NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry
Exercise 8.1- Introduction to Trigonometry
Exercise 8.2 -Introduction to Trigonometry
Exercise 8.3-Introduction to Trigonometry
Exercise 8.4-Introduction to Trigonometry
NCERT solutions of Important Questions-Introduction to Trigonometry
NCERT Solutions for Class 10 Maths Exercise 8.1 of Chapter 8 Introduction to Trigonometry
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
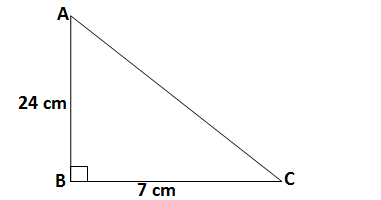
Q1. In ΔABC right angled at B,AB = 24 cm,BC = 7 cm. Determine
(i) sin A, cos A
(ii) sin C, cos C
Ans. The given triangle is ΔABC in which AB = 24 cm, BC = 7 cm and ∠B =90°
Applying Pythagoras theorem
AC = √(AB² + BC²) =√(24² + 7²)=√(576 +49) =√(625) = 25 cm
(i)
(ii)
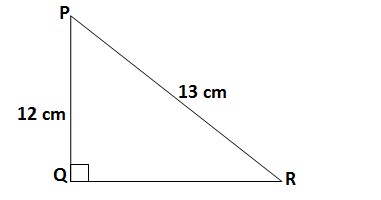
Q2. In the given figure, find tan P – cot R
Ans.In the given ΔPQR, we have PR = 13 cm, PQ =12 cm
Applying Pythagoras theorem
QR = √(PR² – PQ²) = √(13² – 12²) = √(169 -144) = √25 = 5
The value of tan P – cot R
tan P – cot R= 0
Q3.If sin A = 3/4, calculate cos A and tan A
Ans. We are given sin A = 3/4
Since sin A = Perpendicular/Hypotenuse
Let perpendicular = 3x and hypotenuse = 4x
Base = √[(4x)²- (3x)²] = √(16x²-9x²) =x√7
Q4.Given 15 cot A = 8,find sin A and sec A
Ans. We are given that
15 cot A = 8
Let Base is 8x and perpendicular is 15x
Applying pythogorus theorem
Hypotenuse = √(Base² + Perpendicular²) = √[(8x)² + (15x)²]= √(64x² + 225x²)= √(289x²) =17x
Q5. Given sec θ = 13/12, calculate all other trigonometric ratios
Ans. We are given that
Let hypotenuse is 13x and base is 12x
Applying Pythagoras theorem
Perpendicular = √(hypotenuse² – base²) =√(13² – 12²)=√(169-144)=√25 = 5
Q6. If ∠ A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Ans. We are given that
cos A = cos B where ∠A and ∠B are acute angles, the ΔABC must be as follows
Since
cos A = cos B
AC = BC
∠A = ∠B (angles opposite to equal sides in a triangle)
You can see the video for Q1 to Q6 of exercise 8.1
Q7. If cot θ = 7/8,evaluate
(ii) cot²θ
Ans. (i) We are given cot θ = 7/8
Let the base = 7x and perpendicular = 8x
Applying pythogorus theorem
Hypotenuse = √(Base² + Perpendicular²) = √[(7x)² + (8x)²]= √(49x² + 64x²)= √(113x²) =x√113
The given expression
Putting the value of sin θ and cos θ in the given expression
Applying the identity ( x + y)(x -y) = x ² – y²
(ii) The given expression is
cot²θ
Putting the value of cos θ and sin θ
Q8.If 3 cot A = 4, check whether ( 1-tan²A)/(1 +tan²A) = cos²A – sin²A or not
Ans. We are given
3 cot A = 4
Let base = 4x and perpendicular =3x
Applying pythogorus theorem
Hypotenuse = √(Base² + Perpendicular²) = √[(4x)² + (3x)²]= √(16x² + 9x²)= √(25x²) =5x
The value of tan A = p/b = 3x/4x = 3/4, cos A =b/h =4x/5x = 4/5,sin A =p/h=3x/5x = 3/5
Putting the value of tan x, cosx and of sinx in the following equation
LHS = RHS, The equation shown is OK
See the video for Q7 and Q8
Q9. In ΔABC ,right-angled at B ,if tan A = 1/√3 ,find the value of :
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Ans. We are given that tan A = 1/√3
Let BC =x and AB =√3 x
Applying Pythagoras theorem
AC = √(AB² + BC²) = √[(√3x)² + (x)²]= √(3x² + x²)= √(4x²) =2x
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
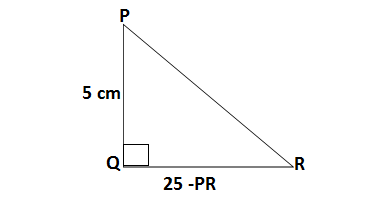
Q10.In ΔPQR ,right angled at Q,PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P,cos P and tan P.
Ans. The given ΔPQR,in which ∠Q=90°, PR + QR = 25 cm and PQ = 5 cm
PR + QR = 25 cm
QR = 25 – PR
Applying Pythogorus theorem
PR² = QR² + PQ²
PR² = (25 – PR)² + PQ²
PR² = 625 + PR²- 50PR + 5²
50PR =650
PR = 13 cm, QR = 25 -13 = 12 cm
sin P = p/h = QR/PR = 12/13
cos P = b/h = PQ/PR = 5/13
tan P = p/h = QR/PQ = 12/5
See the video for Q9,Q10 and Q11
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions of class 9 maths
| Chapter 1- Number System | Chapter 9-Areas of parallelogram and triangles |
| Chapter 2-Polynomial | Chapter 10-Circles |
| Chapter 3- Coordinate Geometry | Chapter 11-Construction |
| Chapter 4- Linear equations in two variables | Chapter 12-Heron’s Formula |
| Chapter 5- Introduction to Euclid’s Geometry | Chapter 13-Surface Areas and Volumes |
| Chapter 6-Lines and Angles | Chapter 14-Statistics |
| Chapter 7-Triangles | Chapter 15-Probability |
| Chapter 8- Quadrilateral |
NCERT Solutions of class 9 science
CBSE Class 9-Question paper of science 2020 with solutions
CBSE Class 9-Sample paper of science
CBSE Class 9-Unsolved question paper of science 2019
NCERT Solutions of class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT solutions of class 10 science
Solutions of class 10 last years Science question papers
CBSE Class 10 – Question paper of science 2020 with solutions
CBSE class 10 -sample paper of science
NCERT solutions of class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions of class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |