NCERT Solutions of Important Questions for Class 10 Maths  Chapter 8 Introduction to Trigonometry

NCERT Solutions of important questions from Class 10 Maths Chapter 8 Introduction To Trigonometry are given here straightforward and well-ordered clarifications. These answers for Introduction To Trigonometry are amazingly well known among Class 10 students for Math Introduction To Trigonometry Solutions convenient for rapidly finishing your homework and getting ready for tests. All questions and answers from the NCERT Book of Class 10 Maths Chapter 8 are given here to you . You will likewise adore the advertisement-free understanding on future study point’s NCERT Solutions of Important questions. All NCERT Solutions of Important Questions for Class 10 Maths are set up by specialists and are 100% precise.

Click for online shopping

Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc

 

NCERT Solutions for Class 10 Maths  Chapter 8 Introduction to Trigonometry

Exercise 8.1- Introduction to Trigonometry

Exercise 8.2 -Introduction to Trigonometry

Exercise 8.3-Introduction to Trigonometry

NCERT solutions of Important Questions-Introduction to Trigonometry

NCERT Solutions of Important Questions for Class 10 Maths  Chapter 8 Introduction to Trigonometry  

For doing all the trigonometric solutions you should have the following formulas in your brain.

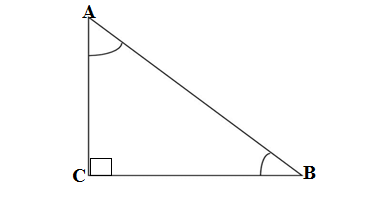
Point to be noticed that here perpendicular means side opposite to the angle and base means side adjacent to the angle, the hypotenuse is the longest side opposite to right angle as in the following fig.

 

 

,      ,     

NCERT Solutions of Important Questions for Class 10 Maths  Chapter 8 Introduction to Trigonometry  

Example –

Express cosθ into all other trigonometric ratios.

Solution- 

transformation into sinθ

The relationship between cosθ and sinθ is given as

sin²θ + cos²θ = 1

cos²θ = 1 – sin²θ

Transformation into tanθ

There is no direct relation between cosθ and tanθ but we know the relationship between cosθ and secθ as following.

…………(1)

Determining the value of secθ in terms of tanθ.

1 + tan²θ = sec²θ

………(2)

Substituting the value of secθ in (1)

Transformation into cotθ 

We have got the cosθ in terms of tanθ

………(1)

We know

………..(2)

Substituting  this value of  tanθ in (1)

Transformation into secθ

There is a direct relationship between cosθ and secθ

Transformation into cosecθ

While expressing cosθ into cosecθ, think over the following fact

………..(1)

Substituting the value of sinθ in (1)

NCERT Solutions of Important Questions for Class 10 Maths  Chapter 8 Introduction to Trigonometry  

Practice exercise-

(1) express sinθ in terms of tanθ.

(2) Write tan θ in phrases of cosecθ.

(3) decide the relationship between secθ and sinθ.

(4) remodel cosecθ into all trigonometric ratios.

(5)express cotθ in terms of secθ.

(1) Hint: sinθ⇒cosecθ⇒cotθ⇒tanθ

(2)Hint:tanθ⇒cotθ⇒cosecθ

(3)Hint:secθ⇒cosθ⇒sinθ

(4)Hint: Check the relationship between cosecθ to other trigonometric ratios one by one.

(5) Hint:cotθ⇒tanθ⇒secθ

Trigonometric Ratios of Complementary Angles-

∠A + ∠B + ∠C = 18O°

∠A + 90° + ∠C =180°

∠A +  ∠C = 180°– 90°

∠A +  ∠C = 90°

∠A & ∠C are complementry to each other

∠C = 90 –∠A

So, comparing the trigonometric ratios corresponding to ∠A, and ∠(90 –A)i.e∠C.

……………(1)

……(2)

From the equations (1) and (2) we have

sin(90–A) = cosA, cos (90– A) = sinA, tan(90–A) = cotA

cot(90–A) = tanA, sec (90– A) = cosecA, cosec(90–A) = sinA

Determining the value of other trigonometric ratio when value of one of them is given-

Table of trigonometric functions for cbse 10 th class

 

Study NCERT solutions for class 10 maths exercise 8.1 Introduction to trigonometry

 

Example-

Find the value of tanθ if

.

sinθ = 7 : 25

 Let perpendicular= 7x and hypotenuse= 25x

Ans.

NCERT Solutions of Important Questions for Class 10 Maths  Chapter 8 Introduction to Trigonometry  

 

Practice exercise- Evaluate the following.

 

(3)   In ΔPQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.

Study A to Z NCERT 10 th class maths solution of lesson 9.1 ‘Some Application Of the Trigonometry’

67° + 23° = 90° and 55° +25° = 90°⇒23= 90 –67 and 25 =90–55, so substituting th values of 23 and 25 in the given expression

(sin²θ +cos²θ=1)

 

(2) If ∠A and ∠B are acute angles such that cosA = cosB then show that ∠A = ∠B.

Answer- Let ΔABC is a right triangle in which ∠A and ∠B are acute angles.

We are given that cosA = cosB

 

AC = BC

∠B = ∠A(angles to equal opposite sides)

See the video for solutions of Q5 part(i),part(ii) and part(iii)  of exercise 8.4 class 10 NCERT maths

 

L.H.S

Substituting sin²θ = 1 – cos²θ

= R.H.S

Solution-

L.H.S

= 2cosecθ= R.H.S

 

(5) Prove that ; (sinα + cosα)(tanα + cotα) = (secα + cosecα)

Solution-

L.H.S

(sinα + cosα)(tanα + cotα)

= cosecα + secα= R.H.S

(6) Prove that

Solution-

L.H.S

= R.H.S

(7) Prove that

Since in the R.H.S we have to get secθ and tanθ so transforming L.H.S in terms of secθ and tanθ, dividing the numerator and denominator by cosθ, we get

Let the [tanθ – secθ] remain in its place at the denominator since in the R.H.S we are to be required this one.

So, multiplying the expressions in the numerators

= R.H.S

(8) Prove that:

L.H.S

= 2secA = R.H.S

(9)

Solution-

L.H.S

=1 + secθ.cosecθ= R.H.S

(10) Prove that:

L.H.S

= secA + tanA = R.H.S

(11) Prove that:

L.H.S

 

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions for class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions for class 9 science 

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

NCERT Solutions for class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT Solutions for Class 10 Science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

NCERT Solutions for class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT solutions for class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals

Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2

Class 12 Maths Important Questions-Application of Integrals

Class 12 Maths Important questions on Chapter 7 Integral with Solutions for term 2 CBSE Board 2021-22

Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22

Solutions of class 12  maths question paper 2021 preboard exam CBSE Solution