Solutions of Class 9 Maths Chapter 12-Heron’s Formula

Solutions of class 9 maths exercise 12.1 of Chapter 12-Heron’s Formula are solved here for the purpose of clearing the doubts of students that are required to get excellent marks in the exam. All solutions of class 9 maths exercise 12.1 of Chapter 12-Heron’s Formula are prepared by an expert of maths who has huge experience in teaching maths subject, each unsolved question of exercise 12.1 is created by a step by step method and as per the CBSE norms therefore every student of 9 class can understand the solutions easily without taking any help from tutor or maths teacher.

Click for online shopping

Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc

NCERT Solutions of class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

Q1.A traffic signal board indicating ‘SCHOOL AHEAD’ is an equilateral triangle with side a. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?

Ans. The side of an equilateral triangle given to us is ‘a’

The sum of its side is = a + a +a = 3a

Semiperimeter of the triagle, s = 3a/2

Since the triangle is equilateral, therefore b=c=a

Applying heron’s formula for calculating its area

If the perimeter of the triangle is 180 cm

a +a +a = 180⇒3a = 180⇒a = 60 m

Area of the triangle

Therefore the area of the triangle is 900√3 cm²

Q2.The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (see figure). The advertisements yield an earning of ₹5000 per m² per year. A company hired one of its walls for 3 months. How much rent did it pay?

Ans.The triangular sides of the wall are,a = 122 m,b=22m, c=120 m

Semiperimeter of the triangular walls,s = (a+b+c)/2 =(122+22+120)/2 =264/2=132

Applying heron’s formula for calculating its area

Putting the value of a,b and c in the formula

=11×2×2×2×5×3 = 1320

Area of the triangular walls is = 1320 m²

The cost of advertisement for hiring 1 year(12 months) = Rs 5000/m²

The cost of advertisement for hiring 3 months = (5000/12)×3 = Rs 1250/m²

The company will pay the rent for 3 months in hiring one of the walls = Area of the triangular walls× 1250= 1320 ×1250 = Rs 1650000

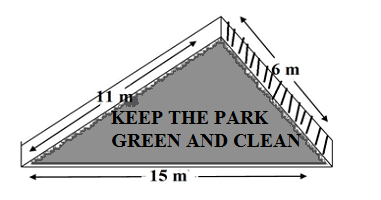
Q3.There is a slide in a park. One of its side company hired one of its walls for 3 months. walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN” (see figure). If the sides of the wall are 15 m, 11 m, and 6m, find the area painted in colour.

Ans.The sides of triangular walls are a = 15 m, b= 11 m and c = 6m

Semiperimeter of the triangular walls,s = (a+b+c)/2 =(15+6+11)/2 =32/2=16

Applying heron’s formula for calculating its area

The area of the triangular wall is 20√2 m²

Q4.Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.

Ans. The given two sides of triangle are ,a = 18 cm and b= 10 cm

Perimeter of the triangle is 42 cm

Third side of the triangle,c = Perimeter -(sum of both sides) =42 -(18+10) =42-28 =14 cm

Semiperimeter,s = Perimeter/2 = 42/2 = 21 cm

Applying heron’s formula for calculating its area

Required area of the triangle is 21√11 cm²

Q5.Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540 cm. Find its area.

Ans. Since the ratio between the sides of triangle given to us is 12:17:25,therefore assuming the sides of triangle 12x, 17x and 25 x

The perimeter given to us = 540 cm

∴ 12x +17x + 25x = 540

54x = 540 ⇒ x =10

Sides of the triangle are,a = 12×10 = 120 cm, b= 17×10=170 cm, c = 25×10=250 cm

Semeiperimeter ,s = Perimeter/2 = 540/2 =270

Applying heron’s formula for calculating the area of triangle

= 100 × 10 ×3×3 = 9000

Therefore required area of the given triangle is 9000 cm²

Q6.An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle

Ans. Each of the equal sides of the isoscell triangle given to us is ,a = b= 12 cm,let the third side of the triangle is c

The perimeter given to us is = 30 cm

∴ c = 30 -(12 + 12) = 30 -24 = 6 cm

Semiperimeter of the triangle is,s = Perimeter/2 =30/2 = 15 cm

Applying heron’s formula for calculating the area of triangle

Therefore the required area of the triangle is 9√15 cm²

Summary of the exercise 12.1 -Heron’s formula

According to Heron’s formula, if the sides of the triangle are a, b .c and the semi perimeter is S , then the area of the triangle is given as follows

Where

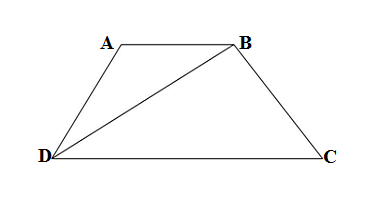
The area of a quadrilateral whose sides and one diagonal is given then it area can also be calculated as follows

Area of the quadrilateral ABCD is = ar ABD + ar DBC

You can compensate us by donating any amount of money for our survival

Our Paytm NO 9891436286

NCERT Solutions of class 9 science

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

CBSE Class 9-Question paper of science 2020 with solutions

CBSE Class 9-Sample paper of science

CBSE Class 9-Unsolved question paper of science 2019

NCERT Solutions of class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT solutions of class 10 science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

Solutions of class 10 last years Science question papers

CBSE Class 10 – Question paper of science 2020 with solutions

CBSE class 10 -Latest sample paper of science

NCERT solutions of class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT solutions of class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals