NCERT Solutions class 9 maths exercise 6.1-Lines and Angles

NCERT solutions class 9 maths exercise 6.1 of chapter 6-Lines and Angles is an easy chapter since the students of 9 class already would have studied Lines and Angles in their previous classes. In this chapter 6- Lines and Angles, the questions are based on lines and angles. All unsolved questions of exercise 6.1 are solved by an expert of maths as per the CBSE norms by a step by step method with a suitable diagram.

Click for online shopping

Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc

NCERT Solutions class 9 maths Chapter 6-Lines and Angles

Exercise 6.1-Lines and Angles

Exercise 6.2-Lines and Angles

Exercise 6.3-Lines and Angles

NCERT Solutions of class 9 maths

Q1.In fig.6.13, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.

Ans. We are given

∠AOC + ∠BOE = 70°

∠BOD = 40°

∠BOD = ∠AOC (Vertically opposite angle)

∴ ∠AOC = 40°

Putting values of ∠AOC in the given equation ∠AOC + ∠BOE = 70°

40 + ∠BOE = 70

∠BOE = 30°

∠AOE + ∠BOE = 180° (Linear pair)

∠AOC + ∠COE + ∠BOE = 180°

40° + ∠COE + 30° = 180°

∠COE = 180° – 70° = 110°

Reflex ∠COE = 360° – ∠COE

Reflex ∠COE = 360° – 110° =250°

Therefore ∠BOE =30° and reflex ∠COE =250°

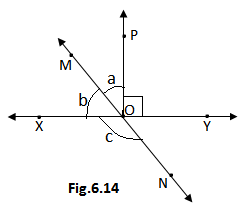
Q2.In fig.6.4 ,lines XY and MN intersect at O .If ∠POY =90° and a: b =2: 3,find c.

Ans.We are given

∠POY =90° and a: b =2: 3

∠POX = 180° – 90° = 90°(Linear pair)

Let a = 2x and b = 3x

∠POX = a + b = 90

2x + 3x = 90

5x = 90°

x = 18°

Therefore a = 2×18 = 36° and b = 3× 18 = 54°

Since MON is a line therefore b and c are linear pair

∴b + c =180°

54° + c = 180°

c = 180° – 54° = 126°

Hence the value of c is 126°

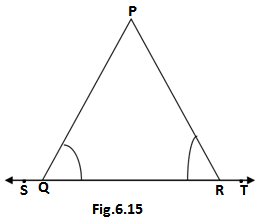
Q3. In fig. 6.15 ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT

Ans.

Given: ∠PQR = ∠PRQ

To Prove: ∠PQS = ∠PRT

Proof: In the given fig.

∠PQS + ∠PQR = 180°(Linear pair)…..(i)

∠PRT + ∠PRQ = 180°(Linear pair)…..(ii)

From equations (i) and (ii)

∠PQS + ∠PQR = ∠PRT + ∠PRQ

∠PQR = ∠PRQ (given)

∠PQS + ∠PRQ = ∠PRT + ∠PRQ

∠PQS = ∠PRT

Hence Proved

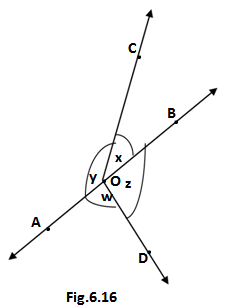
Q4. In fig.6.16 if x +y = w +z, then prove that AOB is a line.

Ans. We have In the given figure

Given: x +y = w +z

To Prove: AOB is a line

Proof: From the figure, we can observe that all the given angles form a complete angle of 360°

Therefore we can write

x +y + w +z = 360° (complete angle)

w + z + w + z = 360°

2w + 2z = 360°

2(w + z) = 360°

w + z = 180

The sum of w and z implies that both angle w and z forms a linear pair, so AOB is a line.

Click-For online purchasing of Computer and Accessories

Q5. In fig.6.17, POQ is a line. Ray OR is perpendicular to line PQ, OS is another ray lying between rays OP and OR. Prove that ∠ROS = 1/2(∠QOS -∠POS).

Ans.

Given: POQ is a line

OR ⊥ PQ

∴ ∠POR = 90° and ∠QOR = 90°

To Prove: ∠ROS = 1/2(∠QOS -∠POS)

Proof: POQ is a line (given)

Therefore ∠POR and ∠QOR are the linear pair

∠POR + ∠QOR = 180°

∠POS + ∠ROS + 90° = 180°

∠POS + ∠ROS = 90°…..(i)

From the fig. we have

∠QOS = ∠QOR + ∠ROS

∠QOS = 90° + ∠ROS

∠QOS – ∠ROS = 90°……(ii)

From (i) and (ii)

∠POS + ∠ROS = ∠QOS – ∠ROS

∠ROS + ∠ROS = ∠QOS – ∠POS

2∠ROS = ∠QOS – ∠POS

∠ROS = 1/2(∠QOS – ∠POS)

Hence proved

Q6.It is given that ∠XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ZYP, find XYQ and reflex QYP.

Ans.

We are given

∠XYZ = 64°

Let ∠PYZ = 2x

∠QYZ = ∠QYP = x ( YQ is the bisector of ∠PYZ)

Since PYX is a line,so

∠PYZ +∠XYZ = 180°

∠QYZ + ∠QYP + 64° = 180°

x + x = 180° – 64° = 116°

2x = 116°

x = 58°,so ∠QYZ = ∠QYP = 58°

∴∠XYQ = ∠XYZ + ∠QYZ = 64° + 58° = 122°

Since ∠QYP = 58°, therefore reflex ∠QYP = 360°-58° = 302°

Hence ∠XYQ = 122° and reflex ∠QYP = 302°

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions for class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions of class 9 science

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

CBSE Class 9-Question paper of science 2020 with solutions

CBSE Class 9-Sample paper of science

CBSE Class 9-Unsolved question paper of science 2019

NCERT Solutions of class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT solutions of class 10 science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

Solutions of class 10 last years Science question papers

CBSE Class 10 – Question paper of science 2020 with solutions

CBSE class 10 -sample paper of science

NCERT solutions of class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT solutions of class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals