NCERT solutions class 9 maths exercise 6.2-Lines and Angles

NCERT solutions class 9 maths exercise 6.2 of chapter 6- Lines and Angles are presented here for helping the class 9 maths students of CBSE in doing their homework and preparation for class tests and the CBSE board exam.NCERT solutions for class 9 maths NCERT of chapter 6 are the most important input material for clearing the doubts on the chapter Lines and Angles which is the basic maths chapter of class 9 maths in the steps of understanding the geometry of class 9 and class 10 level maths. All NCERT solutions of the class 9 maths chapter 6 are created by an expert of maths.

Click for online shopping

Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc

Exercise 6.1-Lines and Angles

Exercise 6.3-Lines and Angles

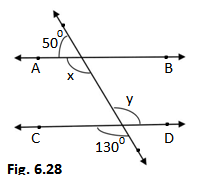
Q1.In fig.6.28, find the values of x and y and then show that AB ll CD.

Ans. It can be observed from the figure that 50° and x forms linear pair

So, x + 50° =180°

x = 180° – 50° = 130°

130° and y forms vertically opposite angles

So, y = 130°

x = y = 130°, implies that interior alternative angles are equal

Since alternative angles are equal, therefore AB ll CD, Hence proved

Q2.In fig. 6.29,if AB ll CD, CD ll EF and y: z = 3 : 7, find x.

Ans.If AB ll CD and CD ll EF

Then AB ll EF

Therefore x = z (alternate angle)

We are given

y: z = 3 : 7

Putting z = x

y : x = 3 : 7

Let y = 3a and x = 7a

y and x are co-interior angles ,so the sum of both x and y is 180°

y + x = 180°

3a + 7a = 180°

10 a = 180°

a = 18

Therefore y = 3×18 = 54° and y =7× 18 = 126°

Hence the value of x is 126°

Q3.In fig.6.30 if AB ll CD, EF ⊥ CD and ∠GED = 126°, find ∠AGE,∠GEF and ∠FGE.

Ans.  We are given that ∠GED = 126°

EF ⊥ CD, so ∠DEF = 90°

∠AGE = ∠GED (alternate angle)

∠AGE =126°

From fig.we have

∠GEF = ∠GED -∠DEF

Putting the value of  ∠GED =126° and ∠DEF= 90°

∠GEF = 126° – 90°= 36°

∠AGE and ∠FGE are linear pair

So,∠AGE + ∠FGE = 180°

Putting the value ∠AGE = 126°

126°+ ∠FGE = 180°

∠FGE = 180° – 126° = 54°

Hence the value of ∠AGE= 126°,∠GEF=36° and ∠FGE= 54°

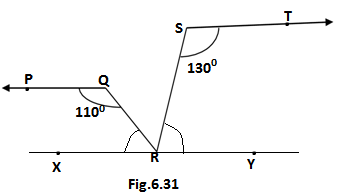
Q4. In fig. 6.31 ,if PQ ll ST,∠PQR = 110° and ∠RST = 130°, find ∠QRS.(Hint: draw a line parallel to ST through point R).

Ans.In the fig. we are given

∠PQR = 110° and ∠RST = 130°

PQ ll ST

Drawing a line XY ll PQ ll ST

Since XY ll PQ and QR is the transversal

∠PQR and ∠QRX are co-interior angles

So,  ∠PQR + ∠QRX = 180°

Putting the value of ∠PQR = 110°

110° +∠QRX = 180°

∠QRX = 180°- 110° = 70°

From the fig. we have

XY  ll ST and SR is the transversal

So,∠RST  and  ∠SRY are the co-interior angles

∠RST  +  ∠SRY = 180°

Putting the value of ∠RST = 130°

130° +  ∠SRY = 180°

∠SRY = 180° – 130°  = 50°

It can be observed in the figure that ∠SRX and ∠SRY are the linear pair

∴ ∠SRX + ∠SRY = 180°

∠QRX + ∠QRS + ∠SRY = 180°

Putting the value of  ∠QRX = 70° and ∠SRY  = 50°

∠QRS + 70° + 50° = 180°

∠QRS + 120° = 180°

∠QRS = 180° – 120° = 60°

Therefore the value of ∠QRS is  60°

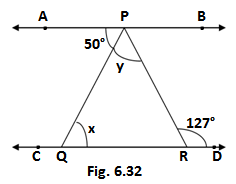
Q5.In fig.6.32 , if AB ll CD, ∠APQ = 50° and ∠PRD = 127°, find x and y.

Ans.We are given in the figure

AB ll CD , ∠APQ = 50° and ∠PRD = 127°

AB ll CD and SR is the transversal, so ∠APR and ∠PRD are the alternates angle

∠APR = ∠PRD

∠APQ + y = 127°

50° + y = 127°

y = 127°- 50° = 77°

AB ll CD and PQ is the transversal, so ∠APQ and ∠PQR are the alternates angle

∠APQ = ∠PQR

x = 50°

Hence the value of x  is 50° and of y is 77°

Click-For online purchasing of Computer and Accessories

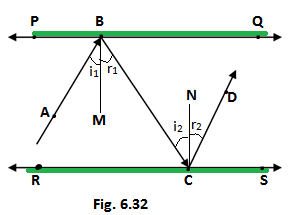
Q6. In fig. 6.33, PQ and RS are the two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB ll CD.

 

 

Ans. We are given the plane mirrors PQ ll RS, the ray AB is incident on PQ and ray CD incident on RS.

Let BM is normal to the plane PQ and CN is normal to the plane RS

Let ∠ABM = i₁, is the incident angle on PQ, r₁ is the reflected angle on PQ, i₂ is the incident angle on RS and r₂ is the reflected angle on RS

PQ and RS can be supposed as  parallel lines and BC as transversal then ∠ABC and ∠BCD are the alternate angles

∴ ∠ABC = ∠BCD

i₁= r₁and i₂= r₂ (incident angle = reflected angle)

BM ⊥PQ and CN ⊥ RS

So, BM ll CN (Perpendiculars on parallel lines are parallel) and BC transversal

Therefore r₁= i₂ (alternate angles)

2r₁= 2i₂

_i1+r₁ =  i₂ + r₂

∠ABC = ∠BCD (alternate angles)

∴AB ll CD

You can compensate us

Paytm number 9891436286

The money collected by us will be used for the education of poor students who leaves their study because of a lack of money.

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions for class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions for class 9 science 

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

NCERT Solutions for class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT Solutions for Class 10 Science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

NCERT Solutions for class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT solutions for class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals

Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2

Class 12 Maths Important Questions-Application of Integrals

Class 12 Maths Important questions on Chapter 7 Integral with Solutions for term 2 CBSE Board 2021-22

Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22

Solutions of class 12  maths question paper 2021 preboard exam CBSE Solution