NCERT Solutions for Class 10 Maths Exercise 15.2 of Chapter 15 Probability

NCERT Solutions for Class 10 Maths Exercise 15.2 of Chapter 15 Probability gives you an idea of solving the questions based on the probability in the CBSE class 10 board maths question paper and other competitive exams maths paper. All the NCERT solutions are created by a qualified maths teacher who has huge experience in teaching mathematics to classes of 9 ,10,11, and 12. These NCERT solutions are solved as per the CBSE norms and updated syllabus of class 10 as prescribed by CBSE.

Click for online shopping

Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc

NCERT Solutions for Class 10 Maths of Chapter 15 Probability

Exercise 15.1-Probability

Exercise 15.2-Probability

NCERT Solutions of class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT Solutions for Class 10 Maths Exercise 15.2 of Chapter 15 Probability

Q1.Two customers Shyam and Ekta are visiting a particular shop in the same week (Tuesday to Saturday). Each is equally likely to visit the shop on any day as on another day. What is the probability that both will visit the shop on
(i) the same day?
(ii) consecutive days?
(iii) different days?

Ans. We are given that Shyam and Ekta visits a particular shop in the same week from Tuesday to Saturday

Let Shyam visits on T,W,Th,F,S and Ekta visits on T,W,Th,F,S

The possible combination of the days they visit the shop in a week are (T,T),(T,W),(T,Th),(T,F),(T,S),(W,T),(W,W),(W,Th),(W,F),(W,S),(Th,T),(Th,W),(Th,Th),(Th,F),(Th,S),(F,T),(F,W),(F,Th),(F,F),(F,S),(S,T),(S,W),(S,Th),(S,F),(S,S),

(i) The outcomes which represents their visits on the same days are (TT),(WW),(Th Th),(FF) and (SS),therefore number of favourable outcomes = 5

Total outcomes are = 25

P(E) = Favourable outcomes/Total possible outcomes

P(Visit on the same day) = 5/25 = 1/5

(ii) The outcomes which represents their visits on consecutive days are (T,W),(W,T),(Th,F),(F,S), number of favourable outcomes = 4

Total possible outcomes = 25

P(Shyam visit the shop on consecutive days) = 4/25

P(Ekta visit the shop on consecutive days) = 4/25

P(Both visit the shop on consecutive days) = 2×(4/25) = 8/25

(iii) The outcomes which represents their visits on different days are (T,W),(T,Th),(T,F),(T,S),(W,T),(W,Th),(W,F),(W,S),(Th,T),(Th,W),,(Th,F),(Th,S),(F,T),(F,W),(F,Th),,(F,S),(S,T),(S,W),(S,Th),(S,F), therefore number of favourable outcomes are =20

P( Their visit on different days) = 20/25 = 4/5

NCERT Solutions for Class 10 Maths Exercise 15.2 of Chapter 15 Probability

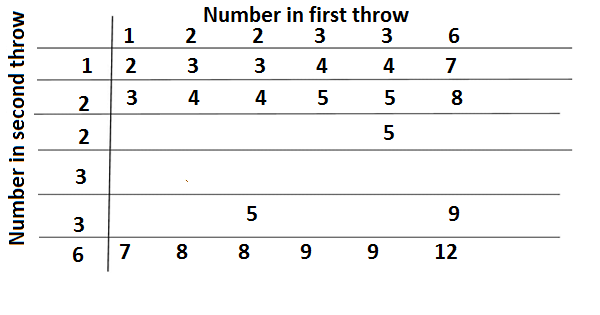
Q2.A die is numbered in such a way that its faces show the number 1, 2, 2, 3, 3, 6. It is thrown two times and the total score in two throws is noted. Complete the following table which gives a few values of the total score on the two throws.

What is the probablity that the total score is

(i) even (ii) 6 (iii) at least 6

Ans.We are given that the dies whose faces show the numbers 1,2,2,3,3,6 are thrown two times,so the outcomes are as follows

(1,1),(1,2),1,2),(1,3),(1,3),(1,6),(2,1),(2,2),2,2),(2,3),(2,3),(2,6),(2,1),(2,2),(2,2),(2,3),(2,3),(2,6)(3,1),(3,2),3,2),(3,3),(3,3),(3,6),(3,1),(3,2),3,2),(3,3),(3,3),(3,6),(6,1),(6,2),6,2),(6,3),(6,3),(6,6),

Total scores in both dies are

(2,3,3,4,4,7),(3,4,4,5,5,8),(3,4,4,5,5,8),(4,5,5,6,6,9),(4,5,5,6,6,9),(7,8,8,9,9,12)

Therefore the complete score tables will be as follows

(i) The outcomes which represent total score even are 2,4,4,4,4,8,4,4,8,4,6,6,4,6,6,8,8,12,therefore favourable outcomes are = 18

Total possible outcomes are = 36

P(score is even) = 18/36 = 1/2

(ii) The outcomes which represent total score 6 are 6,6,6,6, therefore favourable outcomes are = 4

Total possible outcomes are = 36

P(score is 6) = 4/36 = 1/9

(iii)The outcomes which represent total score at least 6 are 7,8,8 6,6,9,6,6,9,7,8,8,9,9,12,,therefore favourable outcomes are = 15

P(at least 6) = 15/36 = 5/12

NCERT Solutions for Class 10 Maths Exercise 15.2 of Chapter 15 Probability

Q3.A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball is double that of a red ball, determine the number of blue balls in the bag.

Ans. Let the number of blue balls in the bag are = x

The number of given red balls in the bag are = 5

Total balls in the bag are = (5 +x)

P(drawing a blue ball) = (number of blue balls)/Total balls = x/ (5 +x)

P(drawing a red ball) = (number of red balls)/Total balls = 5/ (5 +x)

According to question

P(drawing a blue ball) = 2×P(drawing a red ball)

x/ (5 +x) = 2× 5/ (5 +x)

x/ (5 +x) = 10/ (5 +x)

x = 10

Therefore number of blue balls in the bag are 10

NCERT Solutions for Class 10 Maths Exercise 15.2 of Chapter 15 Probability

Q4.A box contains 12 balls out of which x are black. If one ball is drawn at random from the box, what is the probability that it will be a black ball? If 6 more black balls are put in the box, the probability of drawing a black ball is now double of what it was before. Find x

Ans.We are given the number of balls in the bag are = 12

And the number of black balls in the bag are = x

∴P( drawing a black ball) = (number of black balls in the bag)/(Total number of black balls in the bag) = x/12

Since 6 more black balls are put in the box therefore total number of balls in the bag are =12 +6 =18

∴The number of black balls in the bag becomes = (x + 6)

Now,the probability of drawing a black ball is = (x+6)/18

According to question

The probability of drawing a black ball in the second case = 2×The probability of drawing a black ball in first case

(x+6)/18 = 2× x/12

12( x+ 6) = 2x× 18

12x + 72 = 36x

24x = 72

x = 3

NCERT Solutions for Class 10 Maths Exercise 15.2 of Chapter 15 Probability

Q5.A jar contains 24 marbles, some are green and others are blue. If a marble is drawn at random from the jar, the probability that it is green is 2/3. Find the number of blue balls in the jar.

Ans.Let the number of blue balls in the jar are = x

Total number of marbles in the jar are = 24

The number of green marbles in the jar = 24 – x

∴ P( drawing a green marbles) = (number of green marbles)/(Total marbles in the jar)

=(24-x)/24

It is given to us that probability of drawing a green marbles is = 2/3

According to question,we have

(24-x)/24 = 2/3

72 – 3x = 48

3x = 24

x = 8

Therefore the number of blue balls in the jar are 8

NCERT Solutions of class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions of class 9 science

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

CBSE Class 9-Question paper of science 2020 with solutions

CBSE Class 9-Sample paper of science

CBSE Class 9-Unsolved question paper of science 2019

NCERT Solutions of class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT solutions of class 10 science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

Solutions of class 10 last years Science question papers

CBSE Class 10 – Question paper of science 2020 with solutions

CBSE class 10 -Latest sample paper of science

NCERT solutions of class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT solutions of class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals