Class 10 maths NCERT solutions of chapter 13-Surface area and volumes exercise 13.2
Class 10 maths NCERT solutions of chapter 13-Surface area and volumes exercise 13.2
Class 10 maths NCERT solutions of chapter 13 -Surface areas and volumes exercise 13.2 is the chapter of mensuration of class 10 maths NCERT textbook. The NCERT solutions of exercise 13.2 of chapter 13-Surface areas and volumes of class 10 maths are written by an expert CBSE teacher of maths as per the parametric dimension of CBSE board. Class 10 maths NCERT solutions of exercise 13.2 of chapter 13-Surface areas and volumes are written by step by step method, so each student can understand all solutions without getting any help from teachers or tutors.
The exercise 13.2 -Surface area and volume of chapter 13 class 10 maths posses the questions based on the surface area and volume of the combined three-dimensional geometrical figures of cones, spheres, hemispheres, and cylinders. Before you go through the solutions of the questions of exercise 13.2, recall the following formula you have studied in earlier classes.
Total surface area of cylinder =2πr(h +r)
The volume of cylinder = π r²h
Total surface area of cone =πr(l +r)
The volume of cone = 1/3(πrr²h)
The volume of sphere = 4/3(πr³)
The total surface area of hemisphere =3πr²
Volume of hemisphere = 2/3(πr³)
Class 10 maths NCERT solutions of chapter 13-Surface area and volumes exercise 13.2
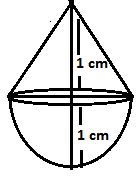
Q1.A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
Ans.
The volume of solid = Volume of hemisphere + Volume of the cone
Radii of cone and hemisphere, r = 1 cm
Height of the cone, h = 1 cm
Volume of hemisphere
Volume of cone
Volume of solid
The volume of solid = π cm³
Class 10 maths NCERT solutions of chapter 13-Surface area and volumes exercise 13.2 question 2
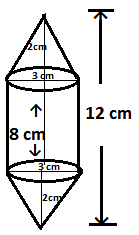
Q2.Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminum sheet. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)
Ans.
The volume of air contained in the model = Total volume of the solid
Total volume of solid = Volume of cylinder + volume of both cones
The diameter of the base of each cone and of cylinder = 3cm
The radius of the base of each cone
Height of each cone = 2cm
Height of the cylinder = 12 – (2+2) = 8 cm
The volume of one cone
The volume of both cones
= 3π cm³
The volume of cylinderical part of the model = π r²h
= 18 π
Vlolume of solid
= 3π + 18 π = 21 π
Hence the volume of the model made by Rachel is = 66 cm³
Class 10 maths NCERT solutions of chapter 13-Surface area and volumes exercise 13.2 question 3
Q3.A gulab jamun contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm.
Ans.
Radius of hemisphere part,r = 2.8/2 = 1.4 cm
Length of the cylindrical part ,h = 5 – (2×1.4) = 2.2 cm and its radius,r = 1.4 cm
Volume of 1 gulab jamun = 2× volume of hemispherical part + volume of cylindrical part
∴ Volume of 45 gulab jamun = 45 × 25.07 = 1128.15 cm³
Since the volume of sugar syrup in gulab jamun = 30%
The volume of sugar syrup in gulab jamun
Therefore sugar syrup in 45 gulab jamun = 338 cm³
Class 10 maths NCERT solutions of chapter 13-Surface area and volumes exercise 13.2 question 4
Q4.A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand.
Ans. We are given ,Length of cuboidal box = 15 cm,Breadth =15 cm, Height = 3.5 cm
Radius of depression,r = 0.5 cm, Height of conical depression,h = 1.4 cm
The volume of wood in pen stand = Volume of cuboidal box – 4× Volume of depression
The volume of cuboidal box = Length × Breadth × Height = 15 × 10 × 3.5 = 525 cm³
The volume of one depression
The volume of 4 depression = 4× 0.367 =1.468 ≈ 1.47
The volume of wood in pen stand = 525 – 1.47 = 523.53≈ 523.5 cm³
Class 10 maths NCERT solutions of chapter 13-Surface area and volumes exercise 13.2 question 5
Q5.A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
Ans.Radius of cone = 5 cm
Height of cone = 8 cm
Volume of water in the cone
Volume of water flows out
Radius of one spherical shot = 0.5 cm [Given]
Volume of one spherical shot
Number of lead shots dropped
Hence number of lead shots dropped on vessels are =100
Class 10 maths NCERT solutions of chapter 13-Surface area and volumes exercise 13.2 question 6
Q6. A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm3 of iron has approximately 8 g mass.
Ans.Given, the height of the big cylinder (H) = 220 cm
Radius of the base (R) = 24/12 = 12 cm
So, the volume of the big cylinder = πR²H
= π(12)² × 220 cm³
= 99565.8 cm³
Now, the height of smaller cylinder (h) = 60cm
Radius of the base (r) = 8 cm
So, the volume of the smaller cylinder =
πr²h
= π(8)2×60 cm³
= 12068.5 cm³
∴ Volyme of iron = Volume of the big cylinder + Volume of the small cylinder
= 99565.8 + 12068.5
= 111634.5 cm³
We know,
Mass = Density × Volume
So, mass of the pole = 8×111634.5
= 893 Kg (aaprox.)
Therefore mass of the pole is ≈ 893 Kg
Class 10 maths NCERT solutions of chapter 13-Surface area and volumes exercise 13.2 question 7
Q7. A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.
Ans
Here, the volume of water left will be = Volume of cylinder – Volume of solid
Given,
Radius of cone.r = 60 cm
Height of cone,h = 120 cm
Radius of cylinder = 60 cm
Height of cylinder,H = 180 cm
Radius of hemisphere,r = 60 cm
Now,
Total volume of solid = Volume of Cone + Volume of hemisphere
The volume of cylinder = π r²H
The volume of water left will be
= 1131428.57 cm³
Hence the volume of water left in the cylinder = 1.131 m³
Class 10 maths NCERT solutions of chapter 13-Surface area and volumes exercise 13.2 question 8
Q8.A spherical glass vessel has a cylindrical neck 8 cm long, 2 cm in diameter; the diameter of the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm3. Check whether she is correct, taking the above as the inside measurements, and π = 3.14.
Ans.
The volume of given vessel = Volume of spherical part + Volume of cylindrical part
We are given radius,r of cylindrical part = 2/2= 1 cm, Height of cylindrical part,h = 8 cm, Radii of spherical part of the vessel,R = 8.5/2 = 4.25 cm
The volume of given vessel
= 3.14(102.354 +8)
= 3.14 × 110.354
= 346.51 cm³
Therefore answer of a child is wrong the right answer of me of the el is 346.51 cm³
You can compensate us
Paytm number 9891436286
The money collected by us will be used for the education of poor students who leaves their study because of a lack of money.
NCERT Solutions of class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for class 9 maths
NCERT Solutions for class 9 science
NCERT Solutions for class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for Class 10 Science
NCERT Solutions for class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions for class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Class 12 Maths Important Questions-Application of Integrals
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution