NCERT Solutions for Class 12 Maths Exercise 10.5 of Chapter 10 Vector Algebra: Miscellaneous Exercise
NCERT Solutions for Class 12 Maths Exercise 10.5 of Chapter 10 Vector Algebra: Miscellaneous Exercise constitutes the summary of the whole chapter 10 of the class 12 maths NCERT textbook.Chapter 10 Vector Algebra: Miscellaneous Exercise is the most important for term 2 CBSE Board exam of class 12 maths because the miscellaneous exercise of vector algebra contains all types of the questions you have studied in exercise 10.1, exercise 10.2, exercise 10.3, and exercise 10.4.Here you can study class 12 maths NCERT solutions free of cost, therefore for any kind of update related to your study, you can subscribe us.
You can also study
Continuity and Differentiability of a function
NCERT Solutions Exercise 10.1 :Vector Algebra
NCERT Solutions Exercise 10.2: Vector Algebra
NCERT Solutions Exercise 10.3 Vector Algebra
NCERT Solutions Exercise 10.4 Vector Algebra
Q1.Write down a unit vector in the XY plane, making an angle of 30° with the positive direction of the x-axis.
Solution: Let us cosider as a unit vector in XY-plane aking an angle θ with the positive direction of x-axis
So,
Here θ = 30°
Hece the required unit vector is
Q2. Find the scalar components and magnitude of the vector joining the points P (x1, y1, z1) and Q (x2, y2, z2).
Solution: The vector joining the points P (x1, y1, z1) and Q (x2, y2, z2) is
The magnitude of the vector is
Hence the scaler components are {(x2– x1 ),(y2– y1 ),(z2– z1 )} and magnitude of is
Q3. A girl walks 4 km towards the west, then she walks 3 km in a direction 30° east of the north and stops. Determine the girl’s displacement from her initial point of departure.
Solution: Let the initial point of the girl is O, from O she walks 4 km towards the west up to the point P, then she walks 3 km in a direction 30° east of the north up to the point Q, it can be shown in the figure below.
As per the figure
Let’s find the displacement during the given journey,i.e
According to the triangular rule of vector addition
Hence, the the girl’s displacement from her initial point of departure is
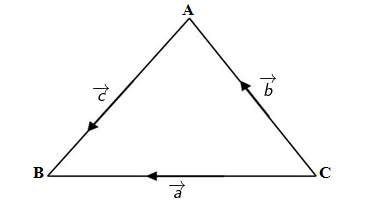
Q4.If ,then it is true that
?
Solution: The given condition is
The given vectors can be drawn as in the following figure
In ΔABC,
By the triangular rule of the addition of the vectors,we have
The magnitudes of the vectors represents the sides of the triangle
Since side of a triangle is always less than the sum of other two sides
Therefore it the given situation is not true.
Q5.Find the value of x for which is a unit vector.
Solution:It is given to us that is a unit vector
±x√3 = 1
x = ±1/√3
Q6.Find a vector of magnitude 5 units, and parallel to the resultant of the vectors
Solution; The given vectors are
Let the resultant vector of the given vectors is
The unit vector in the direction of
Therefore the vector parallel to the resultant vectors of the magnitude 5 units
= ±5×unit vector
Rationalizing denominator
Q7.If , find a unit vector parallel to the vector
Solutions: The given vectors are
A unit vector parallel to the given vector is
Therefore unit vector parallel to the given vector is
NCERT Solutions and CBSE notes for classes 9,10,11 and 12 of Maths and Science
NCERT Solutions and CBSE notes for Class 9,10,11 and 12 of Maths and Science
Download:Direct and Indirect Narration rules Tenses wise and Sentences wise
You can also study
Active Voice to Passive Voice Rules
Learn Tenses in English and translate Hindi sentences into English language
Download PDF-Learn Tenses in English and translate Hindi sentences into the English language
Download: PDFActive Voice to Passive Voice rules,tenses wise and sentences wise
You can also study
Percentage questions for competitive entrance exams with Solutions
NCERT Questions on mensuration helpful for competive entrance exams
Tips to get success in competitive exams
The best books for cracking the competitive entrance exams of CPO,NDA, IAS, CDS and Bank PO
Government jobs after 10 or 12 th pass : Qualify Entrance exams of SSC MTS and SSC CHSL
Science Notes
What is the difference between virtual and real images?
Image formation by Convex and Concave Lenses
Image formation by Convex and Concave Mirrors
Difference between Convex and Concave lenses
What are the factors affecting evaporation?
How does the water kept in an earthen pot become cold during summer ?
Functioning of Soda-Acid Fire Extinguisher
Structure and Function of Cell : Cell Biology
Archimedes Principle: Complete detail
Average Speed and Average velocity
The universal law of gravitational force
Thrust and Pressure : Difference
Evoporation,Vapourization and Latent heat
Important salts class 10 CBSE sceience notes
Reflection, Refraction, Dispersion, and Scattering
Determining Valency, Net Charge and Molecular Formula
Ozone Layer and How it is Getting depleted.
Human Eye – Structure and functions
Myopia, Hypermetropia, and Presbyopia
Electric Current and Heating effect of Electric Current
Complete detail of electrical resistance and conductance
Type of Chemical Reactions with Complete detail
Class 10 chemistry Viva Voce Questions and Answers for CBSE Board 2020-21
What are the physical and chemical properties of metals?
Important maths notes
Tricks – How to write linear equations
Tricks- How to solve question from algebraic equations
Three ways of solving quadratic equation
Solutions- Specific questions of mensuration
Finding the roots of the polynomial by Complete square method
Technics – Achieving 100% marks in Maths
You can compensate us
Paytm number 9891436286
The money collected by us will be used for the education of poor students who leaves their study because of a lack of money.
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions for class 9 maths
NCERT Solutions for class 9 science
CBSE Class 9-Question paper of science 2020 with solutions
CBSE Class 9-Sample paper of science
CBSE Class 9-Unsolved question paper of science 2019
NCERT Solutions for class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for Class 10 Science
Solutions of Class 10 Science Sample Paper and Question Papers for Term-1 and Term 2 2021-22 CBSE Board
Solution of Class 10 Science Question Paper Preboard 2021-22:Term 2 CBSE Board Exam
Solutions of Class 10 Science Sample Paper Term-1 2021-22 CBSE Board
Class 10 Science Sample Paper for Term 2 CBSE Board Exam 2021-22 with Solution
Solutions of Class 10 Science Question Paper Preboard Examination (First) 2021 -22 Class 10 Science
CBSE Class 10 – Question paper of science 2020 with solutions
CBSE class 10 -Sample paper of Science 2020
NCERT Solutions for class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions for class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Class 12 Maths Important Questions-Application of Integrals
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution