NCERT solutions for class 11 maths exercise 9.4 of chapter 9-Sequence and Series

NCERT solutions for class 11 maths exercise 9.4 of chapter 9-Sequence and Series are created for helping the students of 11 class students in clearing their doubts. These NCERT solutions are very important for the students of 11 class students for a better understanding of chapter 9-Sequence and Series. Study of these NCERT solutions will give you a technical idea of solving different types of questions needed in solving the maths question paper in the exams.

Click for online shopping

Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc

NCERT solutions for class 11 maths of chapter 9-Sequence and Series

Exercise 9.1- Sequence and Series

Exercise 9.2 – Sequence and Series

Exercise 9.3 – Sequence and Series

Find the sum to n terms of each of the series in Exercises 1 to 7.

Q1. 1 ×2 + 2 × 3 + 3 × 4 + 4 × 5 +……..

Ans. Observing the first and second number of each term of the series,we can get n^th term a_nof the series as follows.

a_n = n^th term of (1,2,3……) × n^th term of (2,3,4……)

= [1+ (n-1)×1]× [2 + (n -1)×1]

= n × (n +1)

= n² + n

The sum of the series S_nis

S_n= ∑(n² + n)

= ∑n² + ∑n

$=\frac{n\left ( n+1 \right )\left ( 2n+1 \right )}{6}+\frac{n\left ( n+1 \right )}{2}$

$=\frac{n\left ( n+1 \right )}{2}\left [ \frac{2n+1}{3}+1 \right ]$

$=\frac{n\left ( n+1 \right )}{2}\left [ \frac{2n+1+3}{3} \right ]$

$=\frac{n\left ( n+1 \right )}{2}\left ( \frac{2n+4}{3} \right )$

$S_{n}=\frac{n\left ( n+1 \right )\left ( n+2 \right )}{3}$

Q2. 1 × 2 ×3 + 2× 3×4+ 3× 4 ×5+……….

Ans. Observing the first , second and third number of each term of the series,we can get n^th term a_nof the series as follows.

a_n = n^th term of (1,2,3……) × n^th term of (2,3,4……) ×n^th term of (3,4,5……)

= [1+ (n-1)×1]× [2 + (n -1)×1]× [3 + (n -1)1]

n(n + 1)(n + 2) = n(n² +3n +2) = n³ + 3n² +2n

The sum of the series S_nis

S_n=∑ (n³ + 3n² +2n)

= ∑n³ + 3∑n²+ 2∑n

$=\frac{n^{2}\left ( n+1 \right )^{2}}{4}+3.\frac{n\left ( n+1 \right )(2n+1)}{6}+2.\frac{n\left ( n+1 \right )}{2}$

$=n\left ( n+1 \right )\left [ \frac{n\left ( n+1 \right )}{4}+\frac{2n+1}{2}+1 \right ]$

$=n\left ( n+1 \right )\left ( \frac{n^{2}+n+4n+2+4}{4} \right )$

$=n\left ( n+1 \right )\left ( \frac{n^{2}+5n+6}{4} \right )$

Factorizing n² +5n +6

n² + 2n+3n + 6

n (n + 2) + 3(n +2)

(n + 2)(n +3)

$S_{n}=\frac{n\left ( n+1 \right )\left ( n+2 \right )\left ( n+3 \right )}{4}$

Q3.3 ×1² + 5 × 2² + 7 × 3²+……

Ans. Observing the first and second number of each term of the series,we can get n^th term a_nof the series as follows.

a_n = n^th term of (3,5,7……) × n^th term of (1²,2²,3²……)

= [3+ (n-1)×2]× n²

= (2n + 1)n²= 2n³ + n²

The sum of the series S_nis

S_n = ∑(2n³ + n²)

= 2∑n³ +∑ n²

$=2.\frac{n^{2}\left ( n+1 \right )^{2}}{4}+\frac{n\left ( n+1 \right )\left ( 2n+1 \right )}{6}$

$=\frac{n\left ( n+1 \right )}{2}\left [ n\left ( n+1 \right )+\frac{2n+1}{3} \right ]$

$=\frac{n\left ( n+1 \right )}{2}\left [ \frac{3n^{2}+3n +2n+1}{3} \right ]$

$S_{n}=\frac{n}{6}\left ( n+1 \right )\left ( 3n^{2}+5n+1 \right )$

$Q4.\frac{1}{1\times 2}+\frac{1}{2\times 3}+\frac{1}{3\times 4}+......$

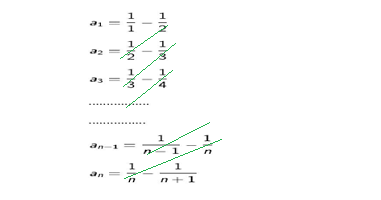
Ans. Observing the pattern of both numbers of denominators of each term.

we can get n^th term a_nof the series as follows.

$a_{n}=\frac{1}{n^{th}\: term\: of\left ( 1,2,3... \right )\times n^{th}\: term\: of\left (2,3,4 ...\right )}$

$=\frac{1}{n\left ( n+1 \right )}$

We can write it in the form

$a_{n}=\frac{\left ( n+1 \right )-n}{n\left ( n+1 \right )}=\frac{1}{n}-\frac{1}{n+1}$

Now,putting n =1,2,3…,we get the series

On adding the terms are canceled out diagonally, we get the sum of the series S_n as follows.

$S_{n}=1-\frac{1}{n+1}$

$S_{n}=\frac{n}{n+1}$

Q5. 5² + 6² + 7²+……..20²

Ans. The given series is 5² + 6² + 7²+……..20²

The sum S_n of the series (5² + 6² + 7²+……..20²) = Sum of the square of first 20 natural number – Sum of the square of first 4 natural number

5² + 6² + 7²+……..20² =( 1² + 2² +3²+4²+ 5²……..20²)-(1² + 2² +3²+4²)

$S_{n}=\sum_{n=1}^{20}n^{2}-\sum_{n=1}^{4}n^{2}$

The sum of the square of first natural number is given as

$=\frac{n\left ( n+1 \right )\left ( 2n+1 \right )}{6}$

$\therefore S_{n}=\frac{20\left ( 20+1 \right )\left ( 2\times 20+1 \right )}{6}-\frac{4\left ( 4+1 \right )\left ( 2\times 4+1 \right )}{6}$

$=\frac{20\times 21\times 41}{6}-\frac{4\times 5\times 9}{6}$

S_n= 2870 – 30 = 2840

Q6. 3 × 8 + 6 × 11 + 9 × 14+……….

Ans. The given series is 3 × 8 + 6 × 11 + 9 × 14+……….

The n^th term of the given series is

= n^th term of (3,6,9…..) × n^th term of (8,11,14…..)

=[3+(n-1)3] × [8 +(n-1)3]

=3n(3n +5) = 9n² +15n

The sum S_n of the series is

S_n = ∑(9n² +15n)

= 9∑n² +15∑n

$=\frac{9n\left ( n+1 \right )\left ( 2n+1 \right )}{6}+\frac{15n\left ( n+1 \right )}{2}$

$=\frac{3n\left ( n+1 \right )}{2}\left [ 2n+1+5\right ]$

$=\frac{3n\left ( n+1 \right )}{2}\left [ 2n+6\right ]$

$=\frac{3n\left ( n+1 \right )}{2}2.\left [ n+3\right ]$

S_n= 3n(n+1)(n+3)

Q7. 1² + (1² +2²) +(1² +2²+ 3²) + ……

Ans. We are given the series

1² + (1² +2²) +(1² +2²+ 3²) + ……

The n^th term of the given series is

(1² +2²+ 3²+……n²)

=∑n²

$=\frac{n\left ( n+1 \right )\left ( 2n+1 \right )}{6}$

$a_{n}=\frac{n\left ( n+1 \right )\left ( 2n+1 \right )}{6}$

$=\frac{1}{6}\left [ (n^{2}+n )\left ( 2n+1 \right )\right ]$

$=\frac{1}{6}\left [ 2n^{3} +n^{2}+2n^{2}+n\right ]$

$S_{n}=\frac{1}{6}\left [ 2\sum n^{3} +3\sum n^{2}+\sum n\right ]$

$=\frac{1}{6}\left [ \frac{2n^{2}\left ( n+1 \right )^{2}}{4}+\frac{3n\left ( n+1 \right )\left ( 2n+1 \right )}{6} +\frac{n\left ( n+1 \right )}{2}\right ]$

$=\frac{n\left ( n+1 \right )}{12}\left [ n\left ( n+1 \right )+2n+1+1 \right ]$

$=\frac{n\left ( n+1 \right )}{12}\left ( n^{2}+n+2n+2 \right )$

$=\frac{n\left ( n+1 \right )}{12}\left ( n^{2}+3n+2 \right )$

Factorizing n² +3n +2 =n² +2n+n +2 =n(n+2) +1(n+2) =(n+2)(n+1)

$S_{n}=\frac{n\left ( n+1 \right )^{2}\left ( n+2 \right )}{12}$

Q8. n(n+1)(n+4)

Ans. We are given the expression of n^th term of the series

n(n+1)(n+4)

Solving it

=n(n² +5n +4)

=n³ + 5n² + 4n

The sum S_n of the series is

S_n = ∑n³ + 5∑n² + 4∑n

$=\frac{n^{2}\left ( n+1 \right )^{2}}{4}+5.\frac{n\left ( n+1 \right )\left ( 2n+1 \right )}{6}+4.\frac{n\left ( n+1 \right )}{2}$

$=n\left ( n+1 \right )\left [ \frac{n\left ( n+1 \right )}{4}+5.\frac{2n+1}{6}+2 \right ]$

$=n\left ( n+1 \right )\left ( \frac{3n^{2}+3n+20n+10+24}{12} \right )$

$=n\left ( n+1 \right )\left ( \frac{3n^{2}+23n+34}{12} \right )$

Factorizing the expression

3n² +23n +34

=3n² + 6n+17n+34

=3n(n+2) + 17(n +2)

=(n+2)(3n +17)

Therefore the sum S_n

$S_{n}=\frac{1}{12}n\left ( n+1 \right )\left ( n+2 \right )\left ( 3n+17 \right )$

Q9. n² +2ⁿ

Ans. We are given n^th term of the series

n² +2ⁿ

Putting n =1,2,3…we get subsequent terms of the series as follows

a₁ = 1²+2¹

a₂ = 2²+ 2²

a₃ = 3² +2³

……………

………….

On adding all the terms we get the sum S_n

S_n= 1²+2¹ + 2²+ 2² + 3² +2³…….

= (1² + 2² +3³ +….) + (2¹ +2² + 2³ +…..)

Since (2¹ +2² + 2³ +…..) is a GP

$=\sum n^{2}+\frac{a\left ( r^{n}-1 \right )}{r-1}$

$=\frac{n\left ( n+1 \right )\left ( 2n+1 \right )}{6}+\frac{2\left ( 2^{n}-1 \right )}{2-1}$

$S_{n}=\frac{n}{6}\left ( n+1 \right )\left ( 2n+1 \right )+2\left ( 2^{n}-1 \right )$

Q10.(2n -1)²

Ans.We are given the expression of n^th term of the series

(2n-1)²

Expading it

=4n² -4n +1

The sum S_n of the series is

S_n = 4∑n² – 4∑n +∑1 (∑1= 1+1+1….upto n terms =n)

$=4.\frac{n\left ( n+1 \right )\left ( 2n+1 \right )}{6}-4.\frac{n\left ( n+1 \right )}{2}+n$

$=n\left ( \frac{2\left ( n+1 \right )\left ( 2n+1 \right )}{3} -2n-2+1\right )$

$=n\left ( \frac{2\left ( n+1 \right )\left ( 2n+1 \right )}{3} -2n-1\right )$

$=\frac{n}{3}\left ( 4n^{2}+6n+2-6n-6+3 \right )$

$=\frac{n}{3}\left ( 4n^{2}-1\right )$

$S_{n}=\frac{n}{3}\left ( 2n-1\right )\left ( 2n+1 \right )$

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions for class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

Study notes of Maths and Science NCERT and CBSE from class 9 to 12

NCERT Solutions for class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions for class 9 science

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

CBSE Class 9-Question paper of science 2020 with solutions

CBSE Class 9-Sample paper of science

CBSE Class 9-Unsolved question paper of science 2019

NCERT Solutions of class 10 maths

Chapter 1-Real number	Chapter 9-Some applications of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT Solutions for Class 10 Science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

Solutions of class 10 last year’s Science question papers

CBSE Class 10 – Question paper of science 2020 with solutions

CBSE class 10 -Latest sample paper of science

NCERT solutions for class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals