Solutions of Class 10 Unit Test -1(2022-23) Mathematics-G.D Lancer’s Public School Delhi
Solutions of Class 10 Unit Test -1(2022-23) Mathematics-G.D Lancer’s Public School Delhi is created here for helping the class 10 students in clearing their doubts about incoming exams and tests. All students of class 10 are needed special attention in mathematics because it is the subject that helps you to increase your aggregate percentage marks in the exam. The solutions of the class 10 Unit Test will give you an idea about the technics of solving the question papers. The unit test of class 10 is presented here is taken from a reputed public school of Delhi G.D Lancer Public School. The solution to the test is created by an expert in maths in a step-by-step way so every student can understand the solution easily. The total questions in this test are 11 and divided into three sections A, B, and C. Section A contains 6 questions and each question is of one mark, section B contains 3 questions and each question is of 2 marks and section C contains 2 questions and each question is of 4 marks. The maximum mark for this maths test is 20.
Solutions of Class 10 Unit Test -1(2022-23) Mathematics-G.D Lancer’s Public School Delhi
Q1.The number √(5+3)/√(5-3) is
(a)Rational number (b) Irrational number
(c)An Integer (d)A natural number
Solution.(a)Rational number
The given number is
√(5+3)/√(5-3)
=√8/√2 = 2√2/√2 =2
2 is a rational number.therefore given number is rational
Q2.If a,b are both positive rational number then is (√a + √b)(√a – √b)
(a)Rational number (b) Irrational number
(c)An Integer (d)both rational as well as irrational
Solution.(a)Rational number
The given number is
(√a + √b)(√a – √b)
Applying the identity (x+y)(x -y) = x² -y²
√a² – √b² = a – b
Since it is given that a and c are positive rational number, according to closure property of rational number (a -b) must be a rational number,therefore the given number is a rational number.
Q3.If am ≠bl then system of equations ax +by = c,lx +my = n has
(a)Unique solution (b) May or may not have solution
(c)Infinitely many the solution (d)no solution
Solution.(a)Unique solution
Since it is given to us
am ≠bl
a/l ≠b/m
⇒a1/a1 ≠b1/b2
Comparing the coefficients of the given pair of the linear equations with the standard pair of the linear equation a1x+b1y +c1=0 and a2x+b2y +c2=0
Q4.Form a quadratic polynomial whose zeroes are 5 +√3 and 5 -√3
Solution.The given zeroes ,α= 5 +√3 and β=5 -√3
The required polynomial is given as
x² -(α +β)x + αβ
x² -( 5 +√3 +5 -√3)x + (5 +√3 )(5 -√3)
x² -10x + (5² -√3²)
x² -10x +(25 -3)
x² -10x +22
Hence the given quadratic polynomial is x² -10x +22
Q5.What number is to be added to the polynomial x² -5x +4, so that 3 becomes the zero of the polynomial
Solution. Let k is added to the given polynomial so that 3 is the zero of the given polynomial x² -5x +4
The polynomial will become
p(x) =x² -5x +4 +k
Then it should satisfy 3 for p(x) =0
3² -5×3 +4 +k =0
9 -15 +4 +k =0
-2 +k =0
k =2
Therefore 2 is added to the given polynomial so that 3 is its zero
Q6.If sum of the zeroes of the polynomial p(x) =(k² -14)x² -2x -12 is 1,then k takes the value
(a)14 (b)-14 (c)2 (d)±4
Solution. (d)±4
The sum of the zeroes is given as
α +β = -b/a, where a is the coefficient of the quadratic term and b is the coefficient of linear term
In the given quadratic equation p(x) =(k² -14)x² -2x -12
a = k² -14, b = -2 and c =-12
α +β = -(-2)/(k²-14)
Since it is given to us α +β =1
1 =2/(k²-14)
k²-14 = 2
k² = 16
k =≠4
Solutions of Class 10 Unit Test -1(2022-23) Mathematics-G.D Lancer’s Public School Delhi
Section-B
Q7.Prove that √5 is irrational.
Ans. Let √5 is a rational number
Where a and b are co-prime number ( study Number system)
b√5 = a
Squaring both sides
5 b² = a²………..(i)
5 is one of the factors of a²
∴ 5 will also be one of the factors of a
Therefore a can be written as a multiple of 5
a = 5c ( where c is another positive integer)
Putting the value of ‘a’ in equation number (i)
5 b² = (5c)² = 25c²
b² = 5c²…………(ii)
5 is one of the factors of b²
∴ 5 will also be one of the factors of b
It is evident from eq.(i) and (ii) that 5 is a common factor in ‘a’ and ‘b’, so it is contrary to the fact we have supposed that √5 is a rational number
Therefore √5 is an irrational number.
Solutions of Class 10 Unit Test -1(2022-23) Mathematics-G.D Lancer’s Public School Delhi
Section-C
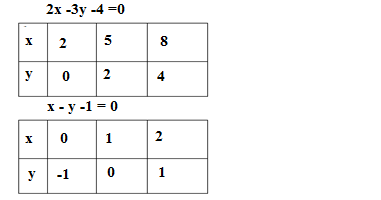
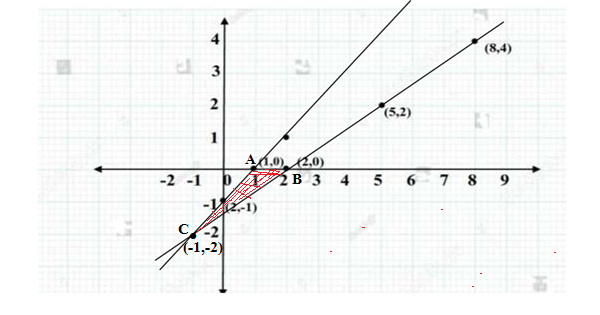
Q10.Solve the following graphically
2x -3y -4 =0
x – y -1 = 0
Shade the triangle between x-axis and given lines.
Solution. The given pair of the linear equation is
2x -3y -4 =0
x – y -1 = 0
The solutions of the equations 2x -3y -4 =0 and x – y -1 = 0 are given as
Now drawing the graph of both equations
The graph of the both equations intersect at (-1,-2),therefore the solutions of the equation is x=-1 and y=-2
Q11.Show that 15n
can not end with the digits 0,2,4,6 and 8 for any natural number
Solution.
The number given is
15n
= (3×5)n
= 3n×5n
3n ×5ncan not end at at 0,2,4,6 and 8 for any value n =1,2,3…. because 3 and 5 both are odd numbers
As an example
If n = 1
then 31×51=15
For n =2
32×52=225
And so on
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions for class 9 maths
NCERT Solutions for class 9 science
NCERT Solutions for class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for Class 10 Science
NCERT Solutions for class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions for class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Class 12 Maths Important Questions-Application of Integrals
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution