Class X th Maths NCERT Solutions of Chapter 9’Some Application of Trigonometry’
Class X th Maths NCERT Solutions of Chapter 9’Some Application of Trigonometry’created here for helping the students of class 10 in boosting their preparation for term-2 CBSE Board exam 2021-22. Class X th Maths NCERT Solutions of Chapter 9’Some Application of Trigonometry’is the most important input study material for clearing the basics of Chapter 9’Some Application of Trigonometry’.The questions in chapter 9 ‘Some Application of Trigonometry’are designed by NCERT as per the prescription of CBSE for class 10 students. All the NCERT Solutions of Chapter 9’Some Application of Trigonometry’are completed by a CBSE maths expert teacher in a step by step way therefore we hope every student of class 10 students can understand these solutions.
Class X th Maths NCERT Solutions of Exercise’Some Application of Trigonometry’
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
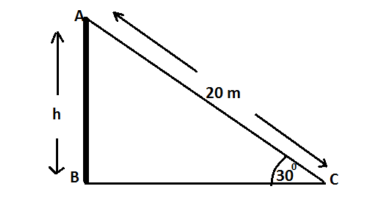
Q.1: A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.
Solution-
The rope is shown as AC and pole by AB
BC =distance of the rope on the ground from the pole
AC = 20m
So, length of pole = 10 m
Class X th Maths NCERT Solutions of Chapter 9’Some Application of Trigonometry’
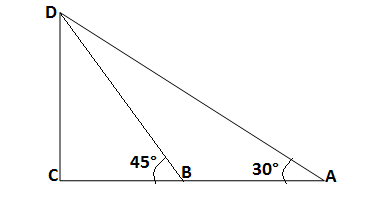
Q.2: A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle
Solution
Let the tree is parted from point C and its top point D contacts the ground at B.
The broken part DC falls on the ground which is appeared by BC making an angle of 30°with the ground.
The length of the tree,AD =BC+DC= AC +BC ( DC =AC)
So for getting the length of the tree, we have to evaluate AC and BC.
………(1)
……..(2)
from (1) and (2) Length of tree
Length of the tree =8√3 m
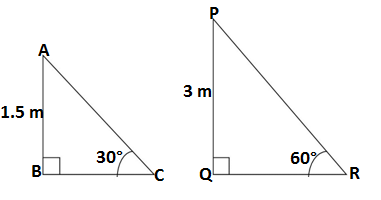
Q.3: A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for the elder children she wants to have a steep side at a height of 3 m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
Solution-
The slide for the children below 5 years is shown by the ΔABC and for elder children by the ΔPQR.
So, considering the ΔABC, the length of the slide= AC
sin 30° = AB/AC
1/2 =1.5/AC
AC = 1.5 × 2
AC = 3
Now considering the ΔPQR, the length of the slide= PR
sin 60° = PQ/PR
√3/2 = 3/PR
PR = 6/√3 = 2√3
Therefore the length of the slides for the children below 5 years is 3m and for elder children is 2√3 m.
Q.4: The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30°. Find the height of the tower.
Solution-
Let the height of the tower is h, the tower is supposed to make an angle of 90°,so the Δ formed with the ground will be right Δ.
The height of the tower will be = 10√3 m
Q.5: A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60° . Find the length of the string, assuming that there is no slack in the string.
Solution-
Length of the string = 40√3 m
Q.6: A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
Solution-
Let the boy is standing initially at a distance of y meter from the foot of the building and walked x meter towards building in such a way that the angle of elevation of the top of the tower from his eyes increases from 30°to 60°.
From the fig.
y = 28.5√3
The initial distance of the boy from the foot point of the building =28.5√3 m
√3(y–x) = 28.5
√3(28.5√3–x) = 28.5
x√3 = 28.5 ×3–28.5
x√3 = 85.5 –28.5 = 57
x = 19√3
So, the boy walked towards the building 19√3 m
Study 8 th lesson of maths and clear your concepts and doubts on 10 th class cbse trigonometry.
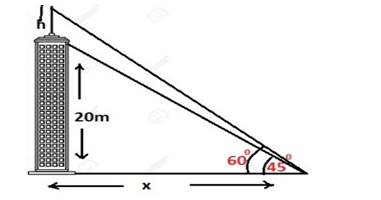
Q.7: From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60°respectively. Find the height of the tower.
Solution-
Let the height of the transmission tower is h, and the distance of the point from the foot point of the building is x
1 ×x = 20
x =20……..(1)
x√3 = 20 +h……(2)
from (1) and (2)
20√3 –20 = h
h = 20(√3 –1)
So, the height of the transmission tower is 20(√3 –1)
Q.8: A statue, 1.6 m tall, stands on a top of pedestal, from a point on the ground, the angle of elevation of the top of statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45° . Find the height of the pedestal.
Solution-
Let the height of pedestal =h
Since the pedestal and statue are vertical to the ground making an angle of 90° , so the horizontal distance to the point of observation and the distance to the top of the statue will make a right Δ.
So, from the fig. we have
⇒h = x
x√3 = h +1.6
h√3 –h = 1.6
h(√3–1) = 1.6
h= 0.8(√3 +1)
Therefore, the height of padestal is 0.8(√3 +1) m.
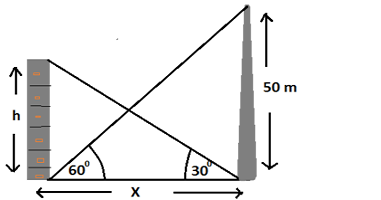
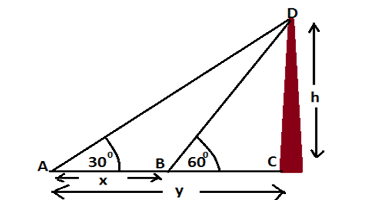
Q.9: The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°.If the tower is 50 m high, find the height of the building.
Solution-
Let the height of the building is = h and the horizontal distance between the building and the tower is = x
Solution-
So, from the fig. we have
……….(1)
x = h√3………..(2)
from (1) and (2)
study the simple tricks of solving the roots of the quadratic equation by the complete squire method.
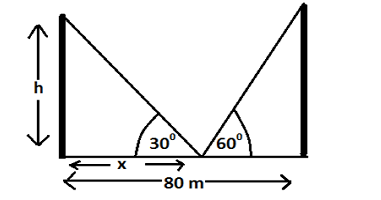
Q.10: Two poles of equal heights are standing opposite each other either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30° , respectively. Find the height of poles and the distance of the point from the poles.
Solution-
Let the height of both poles is = h and the distance of one of the pole is x from the point of observation on the road and of another pole will be = 80–x
So, from the fig. we have
………..(1)
80–x = h√3
………(2)
from (1) and (2) we have
3x = 80–x
x = 20
Therefore the distances of both poles from the point of observation on the road are 20 m and 80–20 =60
Q11.A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30° .Find the height of the tower and the width of the canal.
Solution-
Let DC is the T.V tower, BC is the width of the canal and B is the point on another bank of the canal and A is another point that is 20 meters away from B.
Let DC is a tower, B is a point on another bank of canal and A is a point 20 meter away from point B locatd on the same line that is joining the foot of the tower.
From the fig.
∠A = 30° and ∠DBC = 60°
AC = AB+BC
In ΔBCD
DC = BC√3…. (2)
From equation (i) and (ii)
3BC = 20+BC
BC = 10
Substituting this value of BC in (2) we get
DC = 10√3
Therefore, the hight of tower(DC) is 10√3 m and widh of canal is 10 m.
Q.12: From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Solution-
Let AE is a 7-meter tall building and BD is a cable tower, drawing EC∥AB.
So, AE = BC and CE = AB
In the fig. considering the ΔDCE
DC = CE√3 ………..(1)
CE = BC
BC = 7 (BC = AE)
So, CE = 7, Substituting it in (1)
DC = 7√3
BD = BC + DC = 7 + 7√3 = 7(√3 +1)
Therefore the height of the tower is 7(√3 +1) m.
Q.13: As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45° . If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
Solution-
Let A and B are two ships and lighthouse is DC.
AC = 75√3
In the ΔDCB, we have
BC = DC
BC = 75
SO, the distance between two ships(AB) will be= AC –BC
Therefore the distance between ships = 75√3 –75= 75(√3 –1) m
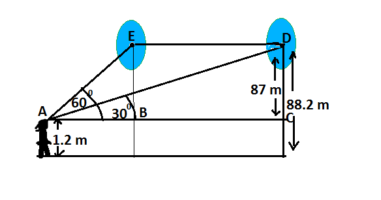
Q.14: A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60° . After some time the angle of elevation reduces to 30°,what will be the distance traveled by the balloon.
Solution-
Let the girl is observing the angle of elevation of 60° when the balloon was on point E and it is reduced to 30°when the balloon reaches D horizontally.
Considering the ΔABE where BE = 88.2 –1.2 = 87 m
…….(1)
From the ΔADC we have
………..(2)
From (1) and (2) we have
BC = AC – AB = 87√3 –87 = 87(√3 –1)
Therefore the distance traveled by the balloon = 87(√3 –1) m
Q.15: A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car as an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60° . Find the time taken by the car to reach the foot of the tower from this point.
Solution-
Let initially the position of the car was A and traveled a distance of x up to B, the height of the tower is h and the distance of the initial position of the car from the point of the tower is y.
In ΔADC, we have
………(1)
In ΔDBC, we have
y√3 –x√3 = h
……(2)
3h = h + x√3
2h =x√3
So, the distance traveled by car in 6s is .
The distance traveled by the car from B to C = y – x = BC is as follows.
BC = y – x
Q.16: The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m, from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Solution-
Let AB is a tower of the height h, C and D are the two points on the ground making the angles of elevation θ and (90 –θ) and located at a distances of 4 m and 9 m respectively from the foot of the tower.
So, from the fig.
In ΔABC
……….(1)
……….(2)
Multiplying (1) and (2)
h² = 36
h = ±6
Neglecting – sign because height is always positive, so the height of the tower will be 6 m.
Class 10 maths ncert solutions chapter 1: Real numbers
Dear students how did you like NCERT solution of the chapter ‘some application of the trigonometry’ please write a comment and ask us the problems you are facing in maths and other subjects, we will resolve it in this platform of future study point. Please subscribe to this web site so that you could get the information about our new published post.
Thanks
You can compensate us by donating any amount of money for our survival
Our Paytm No 9891436286
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions for class 9 maths
NCERT Solutions for class 9 science
NCERT Solutions for class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for Class 10 Science
NCERT Solutions for class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions for class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Class 12 Maths Important Questions-Application of Integrals
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution