NCERT Solutions of class 11 maths exercise 11.1-Conic sections

NCERT Solutions of class 11 maths chapter 11 -Conic sections are the solutions of unsolved questions of the NCERT maths text book of class 11 chapter 11-Conic sections prescribed by CBSE a reputed school board of India.All NCERT Solutions of class 11 maths chapter 11 are solved by CBSE maths expert by a step by step way. All NCERT solutions of class 11 maths chapter 11 are explained here will help all maths students of class 11 and the candidates who are going to appear in competitive entrance exams like NDA,CDS,engineering entrance exams etc .
Download pdf of NCERT solutions class 11 chapter 11-Conic Section
PDF-NCERT solutions class 11 chapter 11-Conic Section
The chapter 11 of NCERT maths text book of class 11 is based on the –Conic Section, Conic Sections contains parabola,ellipse and hyperbola which are the planes carved out from the cone,it is that’s why chapter is named ‘Conic Section’. The questions are based on the equations of all the figure of parabola,ellipse and hyperbola.The chapter ‘Conic Section’ is easy so students can get an excellent score in maths by attempting the questions of chapter 11-Conic Sections in the maths question paper of class 11.
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
Q1.FNCERT Solutions of class 11 maths chapter 11ind the equation of the circle with center (0,2) and radius 2.
Solution. The standard equation of the circle is
(x – h)² + (y – k)² = r²
Where (h,k) are the coordinates of the circle and r is the radius of the circle
It is given that center (h,k) = (0,2) and radius (r)=2
Therefore, equation of the circle is
(x – 0)² + (y – 2)² = (2)²
x² + y² + 4 – 4y = 4
x² + y² – 4y = 0
Q2.Find the equation of the circle with center (-2,3) and radius 4.
Ans. The equation of the circle with centre (h,k) and radius r is given as
(x – h)² + (y – k)² = r²
It is given that center (h,k) = (-2,3) and radius (r)= 4
Therefore, equation of the circle is
(x + 2)² + (y – 3)² = (4)²
x² + 4x² + 4 + y² – 6y + 9 = 16
x² + y² + 4x – 6y – 3 = 0
Q3. Find the equation of the circle with the centre (1/2, 1/4) and radius 1/12.
Ans. The equation of the circle with center (h,k) and radius r is given as
(x – h)² + (y – k)² = r²
It is given that center (h,k) = (-1/2,1/4) and radius (r)= 1/12
Therefore, the equation of the circle is
144x² – 144x+ 36 + 144y² – 72y +9 – 1 = 0
144x² – 144x + 144y² – 72y + 44 = 0
36x² – 36x+ 36y² – 18y + 11 = 0
36x² + 36y² – 36x – 18y + 11 = 0
Q4. Find the equation of the circle with the center (1,1) and radius √2.
Ans. The equation of the circle with center (h,k) and radius r is given as
(x – h)² + (y – k)² = r²
It is given that center (h,k) = (1,1) and radius (r)=√2
Therefore, the equation of the circle is
(x – 1)² + (y – 1)² = (√2)²
x² – 2x +1 + y² – 2y + 1 = 2
x² + y² – 2x – 2y = 0
Q5. Find the equation of the circle with the center (-a,-b) and radius √(a² – b²).
Ans. The equation of the circle with center (h,k) and radius r is given as
(x – h)² + (y – k)² = r²
It is given that center (h,k) = (-a,-b) and radius (r)= √(a² – b²)
Therefore, the equation of the circle is
(x + a)² + (y + b)² = [√(a² – b²)]²
x² + 2ax + a² + y² + 2by + b² = a² – b²
x² + a² + 2ax + y² + b² + 2by = a² – b²
x² + y² + 2ax + 2by + 2b² = 0
Q6. Find the circle and radius of the circle (x + 5)² + (y – 3)² = 36
Ans. The equation of the given circle is
(x + 5)² + (y – 3)² = 36
{x -(- 5)}² + (y – 3)² = 6²
Which is of the form (x – h)² + (y – k)² = r², where h = -5, k = 3, and r = 3.
Thus, the center of given circle is (-5,3) while its radius is 6.
Q7. Find the circle and radius of the circle x² + y² – 4x – 8y – 45 = 0
Ans. The equation of the circle is
x² + y² – 4x – 8y – 45 = 0
(x² – 4x)+ (y² – 8y) = 45
{x² – 2(x)(2) + 2²} + {y² – 2(y)(4) + 4²} – 4 – 16 = 45
(x – 2)² + (y – 4)² = 65
(x – 2)² + (y – 4)² = (√65)²
Which is of the form (x – h)² + (y – k)² = r², where h = 2, k = 4, and r =√65
Thus, the center of the given circle is (2,4), while its radius is √65.
Q8. Find the center and radius of the circle is x² + y² – 8x +10y – 12 = 0
Ans. Standard equation of the circle is
(x – h)² + (y – k)² = r², where (h,k) are the co-ordinates of the centre of the circle.
The given equation of the circle is x² + y² – 8x +10y – 12 = 0
Rewritting the equation of the circle by applying the complete square method
x² – 8x + 4²- 4² + y²+10y +5²-5² – 12 = 0
(x – 4)² + (y + 5)² -16 – 25- 12 = 0
(x – 4)² + (y + 5)² = (√53)²
Comparing the standard equation of the circle
(x – h)² + (y – k)² = r²
h =4, k = -5 and r = √53
Therefore, the centre of the circle is (4,-5) and radius of the circle is √53
Q9. Find the centre and radius of the circle 2x² + 2y² -x = 0
Ans. The given equation of the circle is
2x² + 2y² -x = 0
Rearranging the equation by the method of complete square method
2x² -x + 2y² = 0
Dividing the equation by 2
x² – x/2 + y² = 0
Adding and subtracting the equation by 1/4
x² -x/2 + 1/4 – 1/4 + y² = 0
(x – 1/2)² + (y – 0)² = (1/2)²
(x – 1/2)² + (y – 0)² = (0.5)²
Now, comparing the equation with standard equation of the circle
(x – h)² + (y – k)² = r², where (h,k) are the co-ordinates of the centre of the circle.
Therefore co-ordinates of the centre are (1/2,0) and radius (0.5)
Q10.Find the equation of the circle passing through the points (4,1) and (6,5) and whose centre is on the line 4x + y = 16
Ans. Let the equation of the required circle be (x – h)² + (y – k)² = r²
Since the circle passes through (4,1) and (6,5)
(4 – h)² + (1 – k)² = r²….(i)
(6 – h)² + (5 – k)² = r²….(ii)
Since the centre (h, k) of the circle lies on line 4x + y = 16
4h + k = 16….(iii)
From equations (i) and (ii), we obtain
(4 – h)² + (1 – k)² = (6 – h)² + (5 – k)²
16 – 8h +h² +1 – 2k +k² = 36 – 12h +h² +25 – 10k +k²
16 – 8h +1 – 2k = 36 – 12h +25 – 10k
4h + 8k = 44
h + 2k = 11….(iv)
On solving equations (iii) and (iv), we obtain h = 3 and k = 4
On substituting the values of h and k in equation (i), we obtain
(4 – 3)² + (1 – 4)² = r²
(1)² + (- 3)² = r²
1 + 9 = r²
r² = 10
r = √10
Thus, the equation of the required circle is
(x – 3)² + (y – 4)² = (√10)²
x² – 6x + 9 + y² – 8y + 16 = 0
x² + y² – 6x – 8y + 15 = 0
Q11.Find the equation of the circle passing through the points (2,3) and (-1,1) and whose centre is on the line x – 3y – 11 = 0
Ans. Let the equation of the required circle be (x – h)² + (y – k)² = r²
Since the circle passes thrpugh points (2,3) and (-1,1)
(2 – h)² + (3 – k)² = r²….(i)
(-1 – h)² + (1 – k)² = r²….(ii)
Since the centre (h,k) of the circle lies on line x – 3y – 11 = 0
h – 3k = 11….(iii)
From equations (i) and (ii), we obtain
(2 – h)² + (3 – k)² = (-1 – h)² + (1 – k)²
4 – 4h + h² + 9 – 6k + k² = 1 + 2h + h² + 1 – 2k + k²
4 – 4h + 9 – 6k = 1 + 2h + 1 – 2k
6h + 4k = 11….(iv)
On solving equations (iii) and (iv), we obtain h = 7/2 and k = -5/2
On substituting the values of h and k in equation (i), we obtain
(2 – 7/2)² + (3 + 5/2)² = r²
[(4 – 7)/2)]² + [(6 + 5)/2)]² = r²
(-3/2)² + (11/2)² = r²
9/4 + 121/4 = r²
130/4 = r²
The equation of the required circle is
(x – 7/2)² + (y + 5/2)² = 130/4
[(2x – 7)/2)]² + [(2x + 5)/2)]² = 130/4
4x² – 28x + 49 +4y² + 20y +25 = 130
4x² +4y² – 28x + 20y – 56 = 0
4(x² +y² – 7x + 5y – 14) = 0
x² +y² – 7x + 5y – 14 = 0
∴ The equation of the required circle is x² +y² – 7x + 5y – 14 = 0
Q12.Find the equation of the circle with radius 5 cm whose centre lies on x-axis and passes through the point (2,3)
Ans. The standard equation of the circle is
(x – h)² + (y – k)² = r² where (h,k) are coordinates of the centre and r is the radius of the circle
We know that the radius of the circle is 5 and its centre lies on the x-axis, so coodinates of the centre are (h,k) =(h,0) and r = 5
So now, the equation of the circle is (x – h)² + y ² = 25
It is given that the circle passes through the point (2,3) so the point will satisfy the equation of the circle.
(2 – h)² + 3² = 25
(2 – h)² = 25 – 9
(2 – h)² = 16
2 – h = ± 4
h = 2± 4
h = 6 or -2
The required equation of circle is
(x-6)² +y² =5² or (x + 2)² +k² = 5²
x² + 36 – 12x + y² = 25, x² + 2² +4x +k² = 25
x² – 12x + y² +11=0, x² +4x +k² -21 =0
Q13. Find the equation of the circle passing through (0,0) and making intercepts a and b on the coordinate axes.
Ans.The standard equation of the circle is (x – h)² + (y – k)² = r² where (h,k) are coordinates of the centre and r is the radius of the circle
We are given that circle is passing through (0,0) and making intercepts a and b on the coordinate axes means circle is passing through the point (a,0) on x-axis and (0,b) on y-axis.
substituting (0,0) , (a,0) and (b,0) in the equation of the circle
h² + k² = r²…….(i)
(a -h)² + k²=r²…….(ii)
h² + (b -k)²=r² …….(ii)
from equation (i) and (ii), we have
(a -h)² + k²= h² + k²
a² + h² -2ah + k² = h² + k²
a² – 2ah = 0 ⇒ a(a – 2h) = 0 ⇒a = 0 and a = 2h
a ≠0, so h = a/2
similarly from equation (iii) and (i), we have
(b -k)² + h²= h² + k²
b² + k² -2bk + h² = h² + k²
b² – 2bk = 0 ⇒ b(b – 2k) = 0 ⇒b = 0 and b = 2k
b ≠0, so k= b/2
Now, sbstituting the value of (h,k) =(a/2, b/2) in equation (i)
a²/4 + b²/4 = r²
Putting the value of (h,k) and r in the equation of circle
4x²+ 4y² – 4ax – 4by = 0
x²+ y² – ax – by = 0 is the required equation
Q14.Find the equation of a circle with centre (2,2) and passes through point (4,5).
Ans. The standard equation of the circle is (x – h)² + (y – k)² = r² where (h,k) are coordinates of the centre and r is the radius of the circle
We are given that circle is passing through (4,5) and the coordinates(h,k) of the centre are (2,2)
So,we have r² = (4 -2)² + (5 -2)²= 4 + 9 = 13
r = √13
The equation of the circle is
(x -2)² + (y -2)² =13
x ² + 4 -4x + y² + 4 – 4y = 13
x ² + y² -4x – 4y +8 -13 =0
x ² + y² -4x – 4y -5 =0
Q15.Does the point(-2.5,3.5) lie inside,outside or on the circle x² + y² = 25 ?
Ans. The given equation of the circle is x² + y² = 25
Comparing the given equation with the standard equation of the circle
(x – h)² + (y – k)² = r² where (h,k) are coordinates of the centre and r is the radius of the circle
We get h =0,k =0 and r = 5
Extract of the exercise 11.1 of the chapter 11-Conic Section
The centre of the circle is (0,0) and radius 5 indicates that the point (-2.5,3.5) lies inside the circle since the distance of the point from the centre(0,0) is less than 5 , the radius of the circle.
The circle is the most common geometrical figure in a range of all conic sections. The circle can be driven by slicing a plane parallel to its base and perpendicular to the axis of the cone.
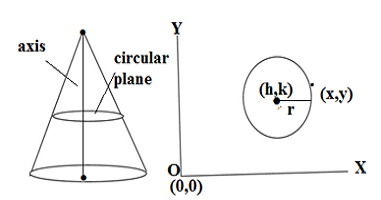
The standard equation of the circle
The standard equation of the circle is
(x – h)² + (y – k)² = r²
Where (h,k) are the coordinates of the circle and r is the radius of the circle
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions for class 9 maths
NCERT Solutions for class 9 science
NCERT Solutions for class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for Class 10 Science
NCERT Solutions for class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions for class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Class 12 Maths Important Questions-Application of Integrals
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution



