NCERT Solutions Class 10 Maths Exercise 12.1 -Areas related to circles
NCERT Solutions Class 10 Maths Exercise 12.1 of Chapter 12-Areas related to circles are the solutions of unsolved questions of NCERT maths text book of class 10 prescribed by CBSE. All NCERT solutions of unsolved questions are created by an expert of future study point. You can study here sample papers, solutions of previous year question papers, tips for the preparation of government entrance exams, and carrier in online jobs.
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
Download pdf of NCERT Solutions of class 10 maths chapter 12-Areas related to circles
Pdf-NCERT solutions of class 10 maths chapter 12-Areas related to Circle
NCERT Solutions for Class 10 Maths Chapter 12-Areas related to circles
Exercise 12.1- Area Related to Circle
Exercise 12.2- Areas related to Circle
Exercise 12.3-Areas Related to the Circle
Q1. The radii of the two circles 19 cm and 9 cm respectively . Find the radius of the circles which has a circumference equal to the sum of the circumferences of two circles.
Ans. Circumference of the circle = 2πr, where r is the radius of the circle and π= 22/7
In the question, we are given the radii of two circles r1 = 19cm ,r2 = 9 cm
Let the radius of the required circle = R
According to question
Circumference of the required circle = Sum of the circumferences of two circles.
2πR = 2πr1+ 2πr2
2πR = 2π(r1 + r2)
R = 19 + 9 = 28
Therefore the radius of the circle is = 28 cm
Q2.The radii of the two circles 8 cm and 6 cm respectively. Find the radius of the circle having an area equal to the sum of the areas of two circles.
Ans.
Area of the circle = πr², where r is the radius of the circle and π= 22/7
In the question, we are given the radii of two circles r1 = 8cm ,r2 = 6cm
Let the radius of the required circle = R
According to question
Area of the required circle = Sum of the areas of two circles.
πR² = πr1²+ πr2²
πR² = π(r1² + r2²)
R²= 8² + 6²= 64+ 36 = 100
R = 10
Therefore the radius of the circle is = 10 cm
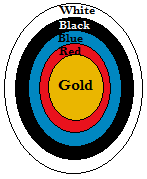
Q3. The given figure depicts an archery target with its 5 scoring areas from the centre outwards as Gold, Red, Blue, Black, and White. The diameter representing the Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.(Use π = 22/7).
Ans. We are given the diameter of circle representing gold region = 21 cm
The radius of gold region is = 21/2 = 10.5 cm
Width of each band of colour is = 10.5 cm
Area of gold region =are of 1 st circle = πr² = (22/7)×10.5 ×10.5 = 346.5 sq.cm
Area of red band = Area of 2 nd circle – Area of 1 st circle
= π[(radius of 2 nd circle)²- (radius of 1 st circle)²]
=22/7[(10.5 +10.5)²- (10.5)²]
22/7[ 21² -(10.5)²]
22/7[ 441 – 110.25]
22/7(330.75) = 22×47.25= 1039.5 sq.cm
Area of blue band = Area of 3 rd circle – Area of 2 nd circle
= π[(radius of 3 rd circle)²- (radius of 2 nd circle)²]
=22/7[(21+10.5)²- (21)²]
22/7[ 31.5² -(21)²]
22/7[ 992.25 – 441]
22/7(551.25) = 22×78.75= 1732.5 sq.cm
Area of black band = Area of 5 th circle – Area of 3 rd circle
= π[(radius of 4 th circle)²- (radius of 3 rd circle)²]
=22/7[(31.5+10.5)²- (31.5)²]
22/7[ 42² -(31.5)²]
22/7[ 1764 – 992.25]
22/7(771.75) = 22×110.25= 2425.5 sq.cm
Area of white band = Area of 5 th circle – Area of 4 th circle
= π[(radius of 5 th circle)²- (radius of 4 th circle)²]
=22/7[(42+10.5)²- (42)²]
22/7[( 52.5)² -(42)²]
22/7[ 2756.25 – 1764]
22/7(992.25) = 22×141.75= 3118.5 sq.cm
Q4. The wheels of a car of diameter 80 cm each . How many complete revolutions does each wheel make in 10 minutes when the car is travelling at the speed of 66 km/h.
Ans. We are given the diameter of the wheel = 80 cm
The radius of the wheel,r = 80/2 = 40 cm
One revolution of the wheels corresponds to the distance traveled by the car= Circumference of the wheel = 2πr = (2×22/7 )40 = 1760/7 cm
The speed of car is given = 66 km/h means the car travels 66 km in 1 h
1h = 60 minutes and 66 km = 66000 m = 6600000 cm
In 60 minutes car travels = 6600000 cm
In 1 minute the car travel = 6600000/60 = 110000 cm
In 1 revolution car travels = 1760/7 cm
The number of revolutions of wheels in 1 minute = The distance traveled by the car in 1 minute/ distance traveled in revolutions
= 110000 ÷ 1760/7
= 110000 × 7/1760
= 437.5 revolutions
In 10 minutes the number of revolutions ,the wheels have = 437.5 ×10 = 4375
Q5.Tick the correct answer in the following and justify your choice. If the perimeter and area of a circle are numerically equal, then the radius of the circle is.
(i) 2 units (ii) π units (iii) 4 units (iv) 7 units
Ans.
Let the radius of the circle is = r
Circumference of the circle is = 2πr
The area of the circle is = πr²
According to question
πr² = 2πr
r = 2
Hence the radius of the circle is 2 units, so the answer is (i) 2 units
ou can compensate us
Paytm number 9891436286
The money collected by us will be used for the education of poor students who leaves their study because of a lack of money.
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions for class 9 maths
NCERT Solutions for class 9 science
NCERT Solutions for class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for Class 10 Science
NCERT Solutions for class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions for class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Class 12 Maths Important Questions-Application of Integrals
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution