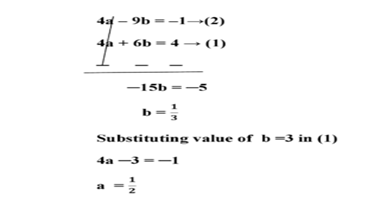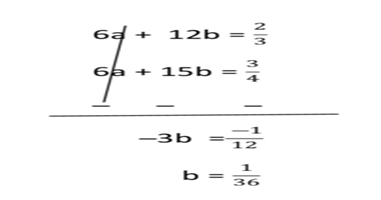Solutions of the most important questions for 10 Class CBSE SA-1 and SA-2

In this post, we have brought for you the most important questions of your NCERT book, as it is clear from the most recent years’ SA-1 and SA-2 exam question papers that the greater number of the questions have been asked , are from NCERT book, After you would have experienced the exercises of NCERT book, repeat these most important questions more than once for getting additional benefits. All questions are fathomed by a subject expert, questions are planned according to the CBSE standards with the goal of perfecting you so you need not be confounded. Design of questions is chosen in an ordered way that will help you in your study plan for SA-1 and SA-2 CBSE board.

Here we have introduced just those questions wherein the majority of the students face a few sorts of troubles, and irrespective of whether you are a genius, normal or week in maths it will support everyone, our principal target is to give you an idea that how might you accomplish the phenomenal performances that you merit. Toward the finish of the post please reveal to us your concern and how did you like these solutions of 10 th class maths solution of most important questions for SA1/SA-2 CBSE board exam.

Solution of Latest Sample paper Class 10 maths for Term 1 2021 CBSE board

Solutions of the most important maths questions for Class 10 CBSE-II

Solutions of the Most important maths questions for Class 10 CBSE for SA-1 and SA2

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

Solutions of most important maths questions for class 10 CBSE-iii

Solutions of the most important questions for 10 Class CBSE SA-1 and SA-2

Click for online shopping

Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc

Q1. Use Euclid’s division lemma to show that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.

Solution-

According to Euclid’s division lemma, any positive integer is written in the form of bq +r where 0 ≤ r < b.

Let b = 3, so possible values of r = 0, 1, 2 (as 0 ≤ r<3)

We get corresponding values of positive integers by placing b=3 and values of r one by one in the expression bq + r.

(3q)² = 3(3q²) = 3m (where m = 3q², another positive integer)

(3q +1)² = 9q² +6q +1 = 3(3q² +2q) +1 = 3m +1(where m = 3q²+2q another positive integer)

(3q +2)² = 9q² +12q +4 = 9q² +12q +3+ 1= 3(3q² +4q +1) +1 = 3m +1(where m = 3q² +4q +1, is another positive integer)

Hence it has been proved that squire of any positive integers either of the form 3m or 3m +1.

Q2. Use Euclid’s division lemma to show that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.

Solution.

According to Euclid’s division lemma, a positive integer is written in the form bq + r where 0 ≤ r < b.

Let b = 9, then 0 ≤ r < 9, so possible values of r will be →0,1,2,3,4,5,6,7,8

Correspoding values of positive intgers are →9q,9q +1, 9q +2, 9q +3, 9q +4, 9q +5, 9q +6, 9q +7, 9q +8

Cubing each term we have

(9q)³ = 9(81 q³) = 9m (where m = 9q³ is another positive integer)

(9q + 1)³ = (9q)³ + 3(9q)² + 3(9q) + 1 = 9(81q³ + 27q² + 3q) + 1 = 9m + 1(where m =81q³ + 27q² + 3q is another positive integer)

(9q +2)³ = (9q)³ +3(9q)²×2 +3×2²×9q +2³= 9(81q³ +54q +12q) +8 = 9m+8 (where m = 81q³ +54q +12q, is another positive integer)

Therefore it is evident from above that cubes of any positive integer is written in the form of 9m or 9m +1 or 9m +8.

Q3.Find a quadratic polynomial, the sum and product of whose zeroes are –3 and 2, respectively.

Solution.

If α and β are the two zeroes of a quadratic polynomial then the quadratic polynomial is expressed as follows.

x² –(α +β)x + αβ

we are given α +β =–3, αβ =2

x² –(–3)x + 2

x²+3x +2

Q4.Obtain all other zeroes of 3x⁴ + 6x³ – 2x² – 10x – 5, if two of its zeroes are √(5/3) and – √(5/3).

Solution.

If two of the zeroes of the given polynomial are √(5/3) and – √(5/3) then [x- √(5/3)] and[x +√(5/3)] will be its two of the factors.

The product of both zeroes = [x- √(5/3)] [x +√(5/3)] = x² – √(5/3)

Therefore the product of both factor will be the factor of the given polynomial so dividing the polynomial by

Factorizing the quotient 3x²+6x + 3

3x² + 3x +3x +3

3x(x +1) + 3(x +1)

(x +1)(3x +1)

x = –1, x = –1/3

Two other zeroes of the given polynomial are –1 and –1/3

Q.5-On dividing x³–3x²+x +2 by a polynomial g(x), the quotient and remainder were (x-2) and (-2x+4) respectively. Find g(x).

Solution.

p(x) = x³–3x²+x +2, q(x) = x-2, r(x) = -2x+4

p(x) = g(x). q(x) +r(x)

g(x) = [p(x) -r(x)]/q(x)

g(x) = [(x³–3x²+x +2) -( -2x+4)/(x-2)

= (x³ -3x² -3x -2)/(x -2)

Therefore g(x) = x³ –x +1

Q6. Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, –7, –14 respectively.

Solution.

If zeroes of a polynomial are given by α, β and γ then the polynomial is written as follows

x³ – (α + β + γ)x² + (αβ + βγ + γα )x – αβγ

α = 2, β=–7, γ = –14

x³ –(2 –7–14)x²+ (2 × –7 –7×–14 –14×2)x + 2×–7×–14

x³ +19x² + 56x +196

Q7.If the zeroes of the polynomial x³ – 3x² + x + 1 are a–b, a, a+b, find a and b.

Solution.

α + β + γ=a –b + a + a + b = 3a

αβ + βγ + γα = (a –b)a + a(a +b) + (a –b)(a +b) =a² +ab +a²+ab +a²–b²= 3a²– b² +2ab

αβγ = (a–b) a (a+b) = a³–ab²

So, the polynomial will be as follows

x³– 3ax² + (3a²– b² +2ab)x – a³+ ab²

Comparing it with the given polynomial x³ – 3x² + x + 1

x³– 3ax² + (3a²– b² +2ab)x – a³–ab² = x³ – 3x² + x + 1

– 3a = –3

a = 1

– a³+ab² = 1

–(1)³ + 1 × b² = 1

b² = 2

b = ±√2

Therefore a = 1, b= ±√2

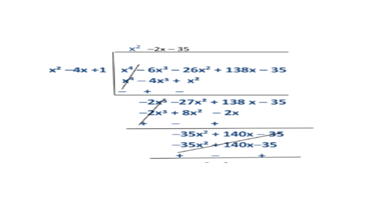
Q8. If two zeroes of the polynomial x⁴ – 6x³ – 26x² + 138x – 35 are 2±√3, find other zeroes.

Solution.

Two zeroes of the polynomial are 2 +√3 and 2 –√3, therefore two of the factors are [x -(2 +√3)] and [x -(2 –√3)]

Hence, one of the factor of the polynomial will be = [x –(2 +√3)][x –( 2 –√3)] =[(x–2 )–√3][(x–2) +√3] = (x –2)² –(√3)² = x² +4 –4x –3 = x² –4x +1

Therefore, dividing the polynomial by x² –4x +1

x²– 2x – 35

x² – 7x + 5x – 35

x(x – 7) + 5(x – 7)

(x – 7)( x + 5)

Therefore its other two zeroes will be x =7 and x = – 5

Q9. If the polynomial X⁴– 6x³ + 16x²– 25x + 10 is divided by another polynomial x² –2x +k the remainder comes out to be x +a find k and a.

Solution.

Comparing it with the reminder given to us

(2k – 9)x + (10 – 8k + k²) = x + a

2k – 9 = 1

k = 5

a =10 – 8k + k² =10 –8 ×5 + 5² = 10–40 + 25 = –5

Therfore value of k = 5 and a = –5

Q10. Solve the following equations

2√x + 3√y = 0

3√x + 2√y = 0

Solution.

The given pair of the equation is

2√x + 3√y = 0 …..(i)

3√x + 2√y = 0 …..(ii)

Multiplying eq.(i) by 2 and eq.(ii) by 3 and then subtracting (i) from (ii)

Substituting the value of y =0 in equation (1) we get x = 0

Solution.

So, equations will become

2a + 3b = 2 → (1)

4a – 9b = –1→(2)

For making the coefficient of ‘a’ equal in both equations, multiplying (1) by 2 and subtracting it from (2)

As we have supposed

So,

Therefore value of x =9 and y = 4

Q12. Solve the following equations

Solution.

Substituting 1/x = a and 1/y = b in the equations (1) and (2) we get following equations (3) and (4)

4a + 3y = 14…….(2), 3a – 4y = 23……..(3)

Multiplying equation (2) by 3 and equation (3) by 4 , we get equation (5) and (6), subtracting equation (6) from (5)

Substituting y = –2, in equation (2)

4a + 3 × –2 = 14

a = 5

As we have supposed

Therefore x = 1/5 and y = –2

Q13.Solve the following equations

Solution.

Substituting 1/(x +y) and 1/(x –y) by a and b we get the equations (3) and (4)

10a + 2b = 4………(3) 15a – 5b = –2…….(4)

Multiplying equation (3) by 5 and equation (4) by 2 we get equation (5) and (6), adding (6) to equation (5)

Putting the value of ‘a’ in the equation (3)

we get b = 1

As we have supposed 1/(x +y) = a and 1/(x –y) = b

So,

x +y = 5……….(7)

x – y =1……….(8)

Adding both of the equation (7) and (8) we get

x =3 and y= 2

Q14. Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current.

Solution.

Let the speed of current = x km/h and the speed of boat in still water is y km/h.
In downstream the speed of boat will be = distance/time= 20/2 = 10 km/h

According to first condition

x + y = 10………..(1)

According to the second condition, the speed of the boat in upstream = distance/time = 4/2 =2 km/h

So,

x – y = 2………(2)

Adding both of the equation (1) and (2)

2x = 12

x =6

Placing the value of x = 6 in (1), we have

y = 4

Therefore speed of boat in still water =4 km/h and speed of current = 6 km/h

Q15. 2 women and 5 men can together finish an embroidery work in 4 days, while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the work, and also that taken by 1 man alone.

Solution.

Let the time taken by 1 woman alone to finish the work = x days and time taken by 1 man alone = y days

x days are the time taken by a woman alone in doing → 1 piece of embroidery work

In 1 day she will do = th part of that work

In 1 day 2 women will do = th part

Y days are the time taken by man alone in doing → 1 piece of embroidery work

In 1 day he will do = th part of that work

In 1 day 5 men will do = th part

It is given to us that 2 women and 5 men finish the work = in 4 day

∴In 1 day they will do = th part

According to first condition the equation will become as following

Similarly, according to the second condition, the equation will be

So, we get the following equations

Multiplying equations (3) by 3 and equation (4) by 2 and then subtracting (3) from (4)

Putting b= 1/36 in equation (3)

putting this value of b = 1/36 in b = 1/y, we get y = 36

Placing the value of a in a = 1/x, we get x = 18

Therefore a woman will take 36 days and a man alone will take 18 days to complete the embroidery work

You can download pdf of most important questions for SA-1/SA-2 from the following link that will definitely help you in achieving your target of excellent marks.

Click for online shopping

Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions for class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions for class 9 science

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

NCERT Solutions for class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT Solutions for Class 10 Science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

NCERT Solutions for class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT solutions for class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals