Solutions of the Most Important Maths Questions of 3 and 4 marks for Class 10 CBSE-Part 3

This article brings the CBSE Class 10 Mathematics: Most Important questions of 3 Marks and 4 marks Questions to get ready for board exams 2021-22.Each question is explained by a step by step method that offers you an idea to display how to solve maths questions in the most ideal manner in the exam.

Mathematics required skill  that can be developed by practicing it. Examining the solutions to a variety of questions is the only way to be perfect in mathematics. We at Future Study Point, furnish students of class 10  a series of  important 3 and 4 marks questions  with solutions  for helping class 10 students . The students who are planning for  achieving  excellent marks in  maths in CBSE Class 10 Board Exam are encouraged to practice the questions given below.

 

In this article Future Study Point is delivering the CBSE Class 10 Mathematics most  Important 3 and 4 Marks Questions for the preparation of CBSE board exam 2021-22. Every one of these questions is totally solved in a systematic and ordered way.

In CBSE Class 10 Mathematics Board Exam 2021-22, Section C and D will involve 10 and 8 questions of 3 and 4 marks each consecutively. In the maths question paper pretty much 65 percent of toatal marks  in class 10 maths paper can be accomplished by trying the 3 and 4 marks questions successfully. Along these lines, if one wishes to surpass desires in the appraisal, an incredible everyday practice with respect to 3 and 4 marks questions are fundamental since the prepration of these questions also accomodate 1 and 2 marks questions.

Here, CBSE class 10 maths most important questions and answers for 2021-22 CBSE board exam – III published by Future Study Point are presented for the students of 10 class who are going to appear in 2021-22 board exam of CBSE.

NCERT Solutions Class 10 Science from chapter 1 to 16

All the questions in CBSE class 10 maths most important questions and answers for 2021-22 board-III are designed by the expert of the maths subject and their answers are readily explained in an ordered way.

These  CBSE class 10 maths most important questions and answers for 2021-21 board-III are designed as per the updated syllabus of CBSE, so you need not to have any kinds of doubt in the selections of the questions. Don’t forget to make a comment and to subscribe us.

Solutions of Most Important Class 10 Maths Questions of 3 and 4 marks Part-1

Solutions of the most important maths questions for Class 10 CBSE-II

Solutions of the Most important maths questions for Class 10 CBSE for SA-1 and SA2

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

Solutions of the Most Important Maths Questions of 3 and 4 marks for Class 10 CBSE-Part 3

Click for online shopping

Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc

Q1.Two taps running together can fill a tank in 3 and 1/13 hr. If one tap takes 3 hours more than the other to fill the tank, then how much time will each tap take to fill the tank?

Solution: Let the time is taken by one of the taps to fill the tank = x hr

∴ In 1 hour it will fill the part of tank = 1/x  part

Time taken by another tap to fill the tank = (x +3) hr

∴ In 1 hour it will fill the part of tank = 1/(x+3)  part

Both of tank will fill the tank in one hour = (1/x) + 1/(x+3)

The part of tank filled by one of the tap to fill the tank in 1 hr + The part of tank filled by another tap to fill the tank in 1 hr = The part of tank filled by both the taps to fill the tank in 1 hr

∴(1/x) + 1/(x+3) = 13/40

(x +x +3)/x(x+3) = 13/40

80x + 120 = 13x² + 39x

13x² – 41x  – 120 = 0

Neglecting minus sign because value of time can not be negative

x = 5

Therefore the time taken by one of the tap is 5 hours and by another tap is (5+3) = 8 hours.

Q2. If  α and β are zeroes of the polynomial P(x) = 3x² +2x + 1, find

See the Video-

Solution: The polynomial given to us = 3x² +2x + 1 with its zeroes α and β

The relationship between zeroes and their coefficients is as follows:

The polynomial corresponding to given zeroes in the question can be driven from the following formula:

x² – (sum of the zeroes)x + product of the zeroes

The sum of zeroes

From (i) and (ii) we have

The product of zeroes

From equation(i) and (ii)

Therefore the sum of the zeroes  and product of the zeroes of the polynomial  = 2 and 3 respectively

So, required polynomial will be = x² – 2x + 3

Q3.If the polynomial  X4 −6×3+ 16×2− 25x + 10   is divided by another polynomial  x²  – 2x + k, the remainders comes out to be x + a,, find k and a.

See the Solution.

CBSE Class lX, X Class, NCERT Solutions and Important questions of Science and Maths

Q4. Prove that the chords of a circle that are equidistant from the center are equal in length.

Solution:

 

GIVEN. A circle with center O, in which there are two chords such that OP ⊥AB and OQ⊥CD and OP =OQ

TO PROVE. AB = CD

PROOF. Joining A and C to O, we get two Δ’s AOP and QOC, so considering both of these Δ’s

AO = CO (radii of the same circle)

OQ = OP (given)

OQ  ⊥ CD, OP ⊥ AB ( OQ and OP are distances of the chords CD and AB from the center O)

∴ ∠OQC = ∠APO= 90°

Δ AOP ≅ ΔQOC ( RHS rule)

CQ = AP ( By CPCT)

2CQ = 2AP( OQ and OP are perpendiculars on both the chords)

∴ CD = AB, Hence proved

Solutions of the Most Important Maths Questions of 3 and 4 marks for Class 10 CBSE-lll

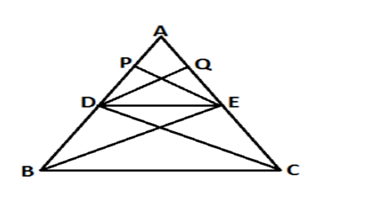
Q5.If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio. Prove it.

Solution.

 

GIVEN: ΔABC, In which BC∥DE

TO PROVE:

CONSTRUCTION: Drawing PE ⊥AB and DQ⊥AC, Joining  C to D and B to E

PROOF. 

From (i) and (ii)

Area of ΔADE in terms of other dimensions

From (iv) and (v) 

arBDE = arDCE (area of Δ’s are equal with a common base and between the same parallel lines)

∴from (vi) we have 

Comparing (iii) and (vii) we have

HENCE PROVED

Q6.Prove that 

Solutions.

LHS

Changing LHS into sin and cos

=RHS

Q7. Prove that

Solutions.

Taking LHS

Since  x³ – y³ = (x -y)( x² + y² +xy)

cos²θ + sin²θ +sinθ.cosθ

= 1 + sinθ.cosθ = RHS, Hence Proved

See the video for most important questions of Trigonometry of Class 10

NCERT Solutions of Science and Maths for Class 9,10,11 and 12

NCERT Solutions for class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron’s Formula
Chapter 5- Introduction to Euclid’s Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions for class 9 science 

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

NCERT Solutions for class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT Solutions for Class 10 Science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

NCERT Solutions for class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT solutions for class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals

Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2

Class 12 Maths Important Questions-Application of Integrals

Class 12 Maths Important questions on Chapter 7 Integral with Solutions for term 2 CBSE Board 2021-22

Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22

Solutions of class 12  maths question paper 2021 preboard exam CBSE Solution