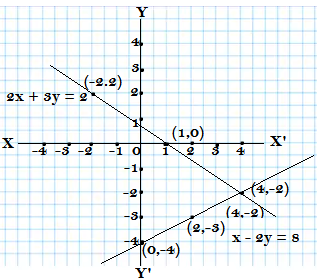Solutions of half-yearly maths question paper of class 10 CBSE 2020
Here you can study the Solutions of the half-yearly maths question paper of 10 class CBSE 2020, the class 10 maths CBSE question paper is taken from one of the reputed schools of Delhi i.e Sanjivani Senior Secondary School of Mohan Garden, New Delhi. Solutions of this question paper will help all the students of class 10 in their preparation for the CBSE annual exam. All questions are solved by an expert teacher of Maths.
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
Solution of Latest Sample paper Class 10 maths for Term 1 2021 CBSE board
Download pdf of solutions of class 10 maths question paper 2020 half yearly exam
Download pdf of solutions of class 10 maths question paper 2020 half yearly exam
Here you can study NCERT solutions of science ad maths from class 9 to 12. You can also study and download important questions of science ad maths, sample papers, previous year’s question papers, government, and other competitive entrance exams, online jobs
Sanjivani Senior Secondary School, Mohan Garden, New Delhi
MM -80
Time-3 hr
Subject-Maths
Class 10 Maths Question Paper CBSE 2022 Half yearly exam with solutions
General Instruction: Read the following instructions very carefully and strictly follow them
(i) This question paper comprises four sections – A, B, C, and D. This question paper carries 40 questions. All questions are compulsory.
(ii) Section A. question number 1 to 20 comprises 20 questions of one mark each.
Section B. question number . 21 to 26 comprises 6 questions of two marks each.
Section C. question number 27 to 34 comprises 8 questions of three marks each.
Section D.question number 35 to 40 comprises 6 questions of four marks each.
SECTION-A
question number 1 to 10 are a multiple-choice questions. Select the correct option.
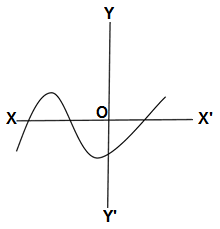
Q1.The graphs of polynomial x = p(y) are given in the figure. Then no of its zeroes is
(a) 3
(b) 1
(c) 2
(d) 4
Ans.(a)
Q2.Which of the following rational number have terminating decimal
Ans.(d)
Q3.The sum and the product of zeroes of a quadratic polynomial are 3 and -10 respectively.The quadratic polynomial is.
(a) x² – 3x + 10
(b) x² + 3x – 10
(c)x² – 3x – 10
(d)x² + 3x + 10
Ans. Applyig the formula for quadratic polyomial
x² – (α + β)x + αβ
Where α and β are the zereoes of the quadratic polynomial given
We are given α + β = 3, αβ = -10
x² – 3x -10
Hence and is (c) x² – 3x – 10
See the video for the solutions of Science Question Paper half yearly exam 2021 Sanjivani Public School
Subscribe us for all updated information
Q4.Write number of solutions of following pair of linear equations
x + 2y -8 = 0
2x + 4y = 16
(a) Unique solution
(b) No solutions
(c) Infinite many solutions
(d) None
Ans.Comparing the coefficients of given pair of linear equations with the coefficients of standard pair of linear equations a1x + b1y + c1= 0 and a2x + b2y + c2= 0
x + 2y -8 = 0, 2x + 4y = 16(rewritten as 2x + 4y -16 = 0)
a1=1 ,b1=2, c1= -8and a2=2 , b2=4 , c2= -16
Since the relationship between the coefficients of both equations are as following
Therefore the given pair has infinite solutions
Q5.Which of the following are quadratic equation ?
(a) x³ + x² + 4 = 0
(b)2x² – 7x = 0
Ans. The equation (a) x³ + x² + 4 = 0 is cubic, the equation (b)2x² – 7x = 0 is quadratic equation, (c) is cubic and (d) is of power 4
Hence the answer is (b)2x² – 7x = 0
Q6. If b² – 4ac ≥ 0 then what would be the roots of the quadratic equation ax² + bx + c = 0
(d) None
Ans. (a)
Q7. Find the common difference of AP.
(a) 2
(b) -2
(c) -3
(d) None
Ans. The given AP is as following
The common difference (d) of the given AP is
Hence the answer is (b) -2
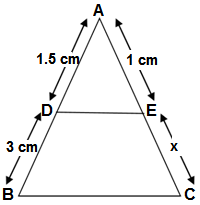
Q8.In figure DE ll BC, find the value of x.
(a) 3 cm
(b) 2 cm
(c) 4 cm
(d) 1 cm
Ans.
In ΔABC we are given DE ll BC, applying the BPT theorem
x = 2
Hence the answer is (b) 2 cm
Q9.Sides of triangles are given below. Determine which of the sides are of right triangles.If the right triangle then finds the length of the hypotenuse.
7 cm, 24 cm and 25 cm
(a) Yes, 24 cm
(b) Yes, 25 cm
(c) No
(d) Yes, 7 cm
Ans.The condition of a triangle being a right triangle is as follows
The square of longest side = sum of the squares of other sides
25² = 24² + 7²
625 = 576 + 49
625 = 625
Therefore the given triangle is right triangle and its hypotenuse is 25 cm
Hence the answer is (b) Yes, 25 cm
Q10. Find 10th term of AP 2, 7, 12……..
(a) 37
(b) 47
(c) 57
(d) None
Ans.
nth term of AP is = a + (n-1)d
a = 2, d = 7-2 = 5 and n = 10
a10 = 2 + (10-1)5
= 2 + 9×5 = 2 + 45 = 47
Therefore the answer is (b) 47
In question number 11 to 15 , fill in blank
Q11. If equation kx -2y = 3 and 3x + y = 5 represent two intersection lines at unique point then value of k is ….
Ans. The given equations are kx -2y = 3 and 3x + y = 5
Writting both equation in standard form
kx -2y – 3=0, 3x + y – 5 = 0
The condition of two lines a1x + b1y + c1= 0 and a2x + b2y + c2= 0 itersecting each other is as follows
Comparing the coefficients of both given lines
a1=k ,b1= -2, c1= -3 and a2=3 , b2=1 , c2= -5
k ≠ -6
The given line has unique solutions for all values of k except to -6
So, answer , k is not equal to -6
Q12.If quadratic equation has equal roots 3x² – 4x + k = 0 has equal roots then value of k is………
Ans. The given equation is 3x² – 4x + k = 0
The condition that the ax² + bx + c = 0 has equal roots is as follows
b² – 4ac = 0
Comparing the given equation with standard equation
a = 3, b = -4 and c = k
(-4)² – 4× 3 ×k = 0
12k = 16
Hence the answer is
Q13. The HCF of two number is 27 and their LCM is 162. If one of the number is 54 . Find other number……..
Ans. We are given HCF of two number = 27 and LCM of two number = 162
One of the number = 54, let another number = x
The relationship between two numbers and their LCM and HCF is as follows
LCM × HCF = Product of both numbers
27× 162 = 54 × x
Therefore another number is 81
Q14. Sum of first n natural number is ……..
Ans. The natural numbers are 1,2,3,4…
First term, a = 1, common difference, d = 1, sum of n terms is = Sn
Putting the value of d = 1, a = 1
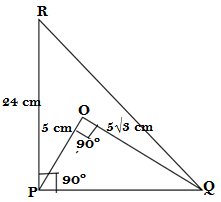
Q15. I fig. OP = 5 cm, OQ = 5√3 cm, ∠POQ = 90°, ∠RPQ = 90° and PR = 24 cm, find RQ……
Ans. In fig. right ΔPQR,we are given PR = 24 cm , In right ΔPOQ , OQ = 5√3 cm, OP = 5 cm
Applying Pythagoras theorem in triangle ΔPQR
RQ² = PQ² + PR²
RQ² = PQ² + 24²
RQ² = PQ² + 576…….(i)
Let’s find the value of PQ from ΔPOQ
In right ΔPOQ
PQ² = OP² + OQ²
PQ² = 5² + (5√3)²
PQ² = 25 + 75
PQ² = 100
Putting the value of PQ in equation (i)
RQ² = 100 + 576
RQ² = 676
RQ = 26
The value of RQ = 26 cm
Question number 16- 20, answer the following
Q16.The nth term of an AP is (7 – 4n), then what is its common difference.
Ans. Let nth is represented by Tn
We are given
Tn= 7 – 4n
T1= 7 – 4×1 = 3
T2= 7 – 4×2 = -1
……
The common difference, d = T2– T1= -1 -3 = -4
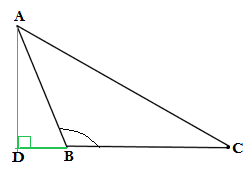
Q17. ΔABC is an isosceles triangle with AC = BC, if AB² = 2AC², then find the measure of ∠C.
Ans. We are given ΔABC is an isosceles
AC = BC
If AB² = 2AC²
AB² = AC² + AC²
Putting AC = BC
AB² = AC² + BC²
Therefore ΔABC is a right triangle in which AB is hypotenuse with sides AC and BC and ∠C
= 90°
Q18.The decimal expansion of will terminates after how many places of decimal.
Ans. We are given the fraction
Converting the denominator into the power of 10, for this multiplying the denominator and numerator by 5
Hence the decimal expansion of the given fraction will terminate after 2 places.
Q19.Form the quadratic polynomial whose zeroes are √2 + 3 and √2 – 3.
Ans. If zeroes of a quadratic polynomial are given as α and β then the quadratic polynomial is given as follows
x² – (α + β)x + αβ
Putting the values α = √2 + 3, β = √2 – 3
x² – (√2 + 3 + √2 – 3)x + (√2 + 3) (√2 – 3)
x² – 2√2 x + √2² – 3²
x² – 2√2 x + 2 – 9
x²- 2√2 x – 7
Hence required quadratic polynomial is x²- 2√2 x – 7
Q20. If -5 is a root of 2x² + px – 15 = 0, find value of p.
Ans. We are given -5 is the root of 2x² + px – 15 = 0
Therefore x = -5 will satisfy the equation 2x² + px – 15 = 0
2×(-5)² + p(-5) – 15 = 0
50 -5p -15 = 0
-5p + 35 = 0
-5p = -35
p = 7
Section B
Question number 21 -26 carry 2 marks each
Q21. Divide the polynomial (9x² + 12x + 10) by (3x + 2).
Ans. Dividing (9x² + 12x + 10) by (3x + 2)
Therefore the quotient is (3x + 2) and the reminder is 6
Q22.Find HCF and LCM of 540 and 72.
Ans. Factorizing the numbers
540 = 2²× 3³×5
72 = 3²× 2³
HCF = 2² ×3² = 36
LCM = 2³×3³× 5 = 1080
Q23. Solve for x and y
x -4y = 1, 2x – 5y = 5
Ans.We are given the equations
x -4y = 1….(i) 2x – 5y = 5…..(ii)
Multiplyig the equation (i) by 2 , we get equation (iii)
2x -8y = 2…….(iii)
Subtractig the equation (iii) form (ii), we get
3y = 3
y = 1
Putting the value y = 1 in equation (i)
x -4× 1 = 1
x = 1 + 4 = 5
Hence,the value of x =5 and y = 1
Q24. Find roots by quadratic formula
4x² + 4√3 x + 3 = 0 OR 2x² + x -4 = 0
Ans. We are given the quadratic equation
4x² + 4√3 x + 3 = 0
Applying the quadratic equation formula
Putting the value a = 4, b= 4√3 and c = 3
Both of the roots of the given equation are -√3/2, -√3/2
Similarily the equation 2x² + x -4 = 0 can be solved by using the quadratic equation formula
Q25.In an AP find missing terms
Ans. We are given second term 13 and fourth term 3
Applying the nth term formula of AP an = a + (n-1)d
a2 = a + (2-1)d, a4 = a + (4-1)d
a2 = a + d, a4 = a + 3d
13 =a + d…..(i) 3 = a + 3d…..(ii)
Subtracting equation (ii) from equation (i)
-2d = 10
d = -5
Putting the value of d = -5 in equation (i)
a -5 = 13
a = 18
Therefore the required term of AP are
18, 13, 8, 3
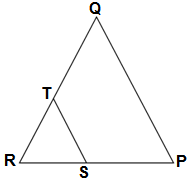
Q26. S and T are points on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ∼ ΔRTS.
Ans.
GIVEN: Δ PQR
S is a point on PR and T is the point on QR
∠P = ∠RTS
CONSTRUCTION: Joining the point T and S, we get a ΔRTS
TO PROVE: ΔRPQ ∼ ΔRTS
PROOF: In ΔPQR and ΔRTS
∠P = ∠RTS (given)
∠R = ∠R (common)
ΔRPQ ∼ ΔRTS (AA rule)
Hence proved
Section C
Question number 27 to 34 carry 3 marks each
Q27. Prove that √3 is an irrational number.
Ans.
Let √3 is a rational number
Where a and b are co-prime number (i.e the numbers who has no common factor except to 1)
b√3 = a
Squaring both sides
3b² = a²……..(i)
It is clear from here that a² is divisible by 3
So, a will also be divisible by 3
Therefore putting a = 3c in equation (i) (where c is another positive integer)
3b² = (3c)² = 9c²
b² = 3c²……(ii)
It is clear from here that b² is divisible by 3
So, b will also be divisible by 3
From equation (i) and equation (ii), we concluded to the point that 3 is a common factor between a and b, hence a and b can’t be co-prime number
Since our assumption that √3 is a rational number is wrong, therefore √3 is an irrational number.
OR
Find HCF of 378, 180, and 420 by the prime factorization method. Is HCF × LCM of three numbers equal to the product of three numbers.
Ans. The given numbers are 378, 180, and 420
Factorizing the numbers
378 = 2 ×3³×7
180 = 2²× 3²×5
420 = 2²× 5×3×7
HCF = 2×3 = 6
LCM = 2²×3³×7×5= 3780
HCF × LCM = 6×3780= 22680
Product of numbers = 378 × 180 ×420 =28576800
HCF × LCM ≠ Product of numbers
Therefore HCF × LCM of three numbers is not equal to the product of three numbers.
OR
Solve graphically 2x + 3y = 2, x – 2y = 8
Ans. We are given the equation 2x + 3y = 2, x – 2y = 8
The solutions of both equations is as following
Solutions of the equation 2x + 3y = 2
| x | 1 | 4 | -2 |
| y | 0 | -2 | 2 |
Solutions of the equation x – 2y = 8
| x | 0 | 2 | 4 |
| y | -4 | -3 | -2 |
Drawing the graph of the equation
Hence both of the lies intersect at(4,-2), so the solution of both equations is (4,-2)
Q28. Solve for x ad y
Ans.
We are given the equations
Let
5a + b = 2……..(iii)
6a – 3b = 1……(iv)
Multiplying the equation (iv) by 5 and equation (iii) by 6 , we get equation (v) and equation (vi)
30 a + 6b = 12….(v) and 30a – 15b = 5…..(vi)
Subtractig equation (vi) from equation (v)
21b = 7
Putting the value of b in equation (iii)
As
x – 1 = 3, y – 2 = 3
x = 4, y = 5
Q29.Find zeroes of quadratic polynomial 6x² + 2 + 7x and verify the relationship between zeroes and coefficients.
Ans. We are given the quadratic polynomial 6x² + 2 + 7x
Rewriting the quadratic polynomial in standard form
6x² + 7x + 2
Factorizing the polynomial by the splitting up method
6x² + 4x + 3x+ 2
2x(3x + 2) + 1(3x + 2)
(3x + 2)(2x + 1)
3x + 2 = 0, 2x + 1 = 0
Therefore zeroes of quadratic polynomial(α and β)
The relationship between zeroes and coefficients of a quadratic polynomial ax² +bx + c are as follows
comparing the equation with standard quadratic equation
a = 6, b = 7, c= 2
Putting the values of a,b,c and zeroes of the polynomial in the relationship formula of zeroes and coefiicients.
Therefore the relationship of zeroes and coefficients is verified
OR
If α and β are zeroes of a quadratic polynomial 4x² + 4x + 1, then form a quadratic polynomial whose zeroes are 2α and 2β.
Ans. We are given the quadratic polynomial 4x² + 4x + 1
The relationship between zeroes(α and β) and coefficients of a quadratic polynomial ax² +bx + c are as follows
Comparing the equation with the standard quadratic equation
a = 4, b = 4 and c = 1
Puttig the values in the relationship formula
α + β = -4/4 and αβ = 1/4
α + β = -1….(i) αβ = 1/4…..(ii)
Let’s find out the quadratic polynomial whose zeroes are 2α and 2β by the following formula
x² -(sum of zeroes)x + product of zeroes
x² -(2α+ 2β)x + 2α×2β
x² -2(α+ β)x + 4 αβ
Putting the values of α+ β and αβ
x² -2(-1) x + 4 ×1/4
x² + 2x + 1
Hence the required quadratic polynomial is x² + 2x + 1
Q30.Find the roots of the equations
Ans. The given equation is
Simplifying it to get the standard quadratic equation
11x² -33x – 308 = -330
11x² -33x – 308 + 330 = 0
11x² -33x + 22 = 0
Factorisig it by splitting method
11x² -22x -11x + 22 = 0
11x(x – 2) – 11(x – 2) = 0
(x – 2) (11x -11) = 0
x = 2, x = 1
Hence the solution of the given equation is x = 2, x = 1
Q31.Which term of AP 3,15,27,39…….. is 132 more than its 54th term.
Ans. The given AP is 3,15,27,39……..
The first term, a of AP is = 3, common difference, d = 15-3 = 12
Let nth term of given AP is 132 more than its 54th term.
an= a54+ 132
a + (n-1)d = a + 53d + 132
(n-1)d – 53d = 132
d(n –1 -53) = 132
12(n – 54) = 132
n – 54 = 132/12
n = 54 + 11 = 65
Hence 65th term is 132 more than the 54th term of the given AP
OR
In an AP, given a = 3, n = 8, S = 192, Find d
Ans. We are given a = 3, n = 8, S = 192
Applying the formula for sum of an AP
4(6 +7d) = 192
24 + 28d = 192
28d = 192 – 24 = 168
d = 4
Hence the value of d is 4
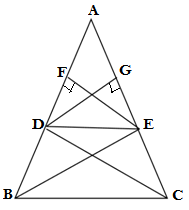
Q32. If a line is drawn parallel to one side of a triangle to intersect other two sides in district points .Prove that the other two sides are divided in the same ratio.
Ans.
GIVEN: ΔABC in which DE ll BC
CONSTRUCTION: Drawing EF ⊥ BD and DG ⊥ AC
TO PROVE:
PROOF: Triangles ΔDBE and ΔDEC made on the same base and between the same parallel lines
∴arΔDBE = ar ΔDCE……(i)
arΔADE = 1/2 AD×EF
arΔDBE = 1/2 BD×EF
arΔADE = 1/2 DG×AE
arΔDCE = 1/2 CE×DG
Dividing equation (ii) by equation (iii)
From equation (i) arΔDBE = ar ΔDCE
AD × CE = BD × AE
Hence proved
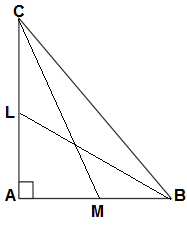
Q33. BL and CM are median of a triangle ABC, right-angled at A.
Prove that 4(BL² + CM²) = 5 BC².
Ans.
GIVEN: ΔABC in which
∠A = 90°
BL and CM are median of a Δ ABC
TO PROVE: 4(BL² + CM²) = 5 BC²
PROOF: Applying the Pythagoras theorem in right ΔABC, ΔAMC and ΔABL
BC² = AB² + AC²…….(i)
CM² = AM² + AC²….(ii)
BL² = AB² + AL²…..(iii)
Adding equation number (ii) and (iii)
CM² + BL²= AM² + AC² + AB² + AL²
From equation number (i) AC²= BC² -AB²
CM² + BL²= AM² + BC² -AB² + AB² + AL²
CM² + BL²= AM² + BC² + AL²
AM = AB/2 (CM is the median of the ΔABC on BC)
AL = AC/2 (BL is the median of ΔABC on AC)
CM² + BL² = AB²/4 + BC² + AC² /4
Multiplying both sides by 4
4 (CM² + BL²) = AB² + 4BC² + AC²
4 (CM² + BL²) = 4BC² + AC²+ AB²
Substituting from equation (i) BC² = AB² + AC²
4 (CM² + BL²) = 4BC² + BC²
4 (CM² + BL²) = 5BC² , Hence proved
Q34. Solve for x
Ans. We are given the equation
(3x + 4)(x + 4) = 4(x² + 3x + 2)
3x² + 12x + 4x + 16 = 4x² + 12x + 8
4x² -3x² – 4x -8 = 0
x² -4x -8 = 0
Factorising it by quadratic formula
x = 2 ±2√3
Hence x = 2 + 2√3, 2 – 2√3 are the required solutions of the given equation
OR
Yash scored 40 marks in a test getting 3 marks for each right answer and losing 1 mark for each wrong answer . Had 4 marks been awarded for each correct answer and 2 marks been deducted for each incorrect answer ,then Yash would have scored 50 marks . How many questions were there in the test.
Ans. Let Yash answered the questions correctly = x and answered the questions incorrectly = y
According to first condition of the question
3x – y = 40……(i)
According to second condition of the question
4x -2y = 50….(ii)
Multiplying equation (i) by 2, we get equation (iii)
6x -2y = 80…..(iii)
Subtracting equation (iii) from equation (ii)
-2x = -30
x = 15
Putting x = 15 in equation (i)
3×15- y = 40
45-y = 40
y = 5
The solutions of the equation is x = 15 and y = 5
Number of questions Yash answered correctly = 15 and answered incorrectly = 5
Hence total number of questions in the test were = x + y = 15 + 5 = 20
Section D
Question numbers 35 to 40 carry 4 marks each.
Q35. If 4 times the 4th term of an AP is equal to 18 times the 18th term ,then find 22 nd term.
Ans. nth term of an AP is given by
an = a + (n -1) d
Where a is first term, d is the common difference of an AP
We are given in the question
4 times the 4th term of an AP is = 18 times the 18th term
4[a + (4-1)d ]=18[a + (18 -1)d]
4a + 12d = 18a +306d
294d = -14a
21d = -a
a = -21d
Now,22nd term = a + 21d
Putting the value a = -21d
22nd term = -21d+ 21d = 0
Hence the 22nd term of the AP is 0.
OR
How many terms of AP 24, 21, 18…..must be taken so that their sum is 78.
Ans. The given AP is 24, 21, 18….
Common difference of the given AP,d is = 21 -24 = -3 and first term, a = 24
Let the number of terms whose sum is 78 are = n
Applying the following formula for the sum(S) of an AP
We are given S = 78
(51 – 3n)n =156
-3n² + 51n = 156
3n² – 51n + 156 = 0
n² – 17n + 52= 0
Factorising it by splitting up method
n² – 13n -4n+ 52= 0
n(n -13) – 4(n – 13) = 0
(n – 13)(n -4) = 0
n = 13, n = 4
Therefore the number of terms are either 13 or 4 whose sum is 78.
Q36.In an obtuse ΔABC, ∠B is obtuse AD is perpendicular to CB produced,then prove that AC² = AB² + BC² + 2BC.BD
Ans.
GIVEN: In an obtuse ΔABC, ∠B is obtuse
AD ⊥CB
TO PROVE:AC² = AB² + BC² + 2BC.BD
PROOF: In ΔADB and ΔADC, applying the Pythagoras theorem
AC² = DC² + AD²…..(i)
AB² = AD² + BD²…..(ii)
Subtracting equation (ii) from equation (i)
AC² – AB² = DC² – BD²
In figure, we have DC = BD + BC
AC² – AB² = (BD + BC)² – BD²
AC² – AB²= BD² + BC² + 2BC.BD – BD²
AC² – AB² = BC² + 2BC.BD
AC² = AB² + BC² + 2BC.BD, Hence proved
OR
The perpendicular from A on side BC of a ΔABC intersect BC at D, such that DB = 3CD,prove that 2AB² = 2AC² + BC²
Class 10 Maths NCERT Solutions from chapter 1-15
Q37.Solve for x
Ans. The given equation is
ax + bx +x² = -ab
x² + ax + bx + ab = 0
x(x + a) + b( x +a) = 0
(x + a)(x + b) = 0
x = -a, -b
Hence the solutions of the equation is x = -a and x = -b
Q38.A boat takes 4 hr to go 44 km downstream and it can go 20 km upward in the same time . Find speed of stream and that of the boat in still water.
Ans.Let the speed of boat in still water = x and speed of stream = y
The speed of the boat in downward stream = speed of boat + speed of stream=x+y
The speed of the boat in downward stream = Distace covered in downwardstream/Time taken = 44/4 = 11 km/h
∴ x + y = 11……(i)
The speed of the boat in upward stream = speed of boat -speed of stream=x-y
The speed of the boat in downward stream = Distance covered in upward stream/Time taken = 20/4 = 5 km/h
∴ x – y = 5……(ii)
Adding equation (i) and (ii)
2x = 16
x = 8
Putting the value of x in equation (i)
8 + y = 11
y = 3
Hence the speed of boat in still water is 8 km/h and speed of stream is 3 km/h
Q39. Find all zeroes of 2x4– 3x3-3x2+ 6x -2, if two of its zeroes are √2 and -√2.
Ans. We are given the polynomial 2x4– 3x3-3x2+ 6x -2
If two of zeroes are √2 and -√2 then (x -√2)(x +√2) =x² -2 will be one of its factor.
Therefore further factorizing the polynomial by the reminder’s theorem
2x4– 3x3-3x2+ 6x -2
2x2(x² -2) +4x²- 3x(x²-2)-6x-3x²+ 6x -2
2x2(x² -2) – 3x(x²-2)-3x² +4x²-3x²- 2
2x2(x² -2) – 3x(x²-2) + (x² – 2)
(x² -2)(2x2 – 3x +1)
(x² -2)[2x2 – 2x-x +1]
(x² -2)[2x(x -1) -1(x -1)]
(x² -2)(x -1)(2x -1)
(x² -2) = 0⇒x =±√2, x =1 and x = 1/2
Hence other two zeroes of the given polynomial are 1 and 1/2
Q40. Prove that 1/√2 is an irrational number.
Ans. Let 1/√2 is a rational number
So, 1/√2 = a/b (Where a and b are co-prime numbers)
a√2 = b
Squaring both sides
2a² = b²……(i)
b² is divisible by 2
∴ b is also divisible by 2
b is also written in the form of 2c, where c is another positive integer
b = 2c
Putting b = 2c in equation (i)
2a² =(2c)²= 4c²
a² = 2c²……(ii)
a² is divisible by 2
∴ a is also divisible by 2
Equation (i) and equation (ii) implies that 2 is a common factor between a and b,so our assumption is wrong that a and b are co-prime number
Therefore 1/√2 can’t be a rational number, so 1/√2 is an irrational number
What are the physical and chemical properties of metals?
Class 10 Science NCERT Solutions from Chapter 1 to 16
You can compensate us by donating any amount of money for our survival
Our Paytm NO 9891436286
You can compensate us
Paytm number 9891436286
The money collected by us will be used for the education of poor students who leaves their study because of a lack of money.
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions for class 9 maths
NCERT Solutions for class 9 science
NCERT Solutions for class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for Class 10 Science
NCERT Solutions for class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions for class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Class 12 Maths Important Questions-Application of Integrals
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution