NCERT Solutions of class 9 Maths exercise 7.1 – Triangles
NCERT Solutions of class 9 Maths exercise 7.1 of chapter 7- Triangles are the solutions of unsolved questions of class 9 NCERT maths textbook, these NCERT solutions are solved by an expert of maths as per the CBSE norms. The NCERT solutions of exercise 7.1 of chapter 7-Triangles are based on the congruency of the triangle. Every year one or two questions of 3 to 4 marks are always asked from this exercise 7.1, so it is very important for class 9 students to study NCERT solutions of exercise 7.1.
Click for online shopping
Future Study Point.Deal: Cloths, Laptops, Computers, Mobiles, Shoes etc
NCERT Solutions of Class 9 Science : Chapter 1 to Chapter 15
Q1.In quadrilateral ACBD, AC = AD, and AB bisect ∠A (see the given figure). Show that ΔABC≅ΔABD. What can you say about BC and BD?
Ans.
GIVEN:In quadrilateral ACBD, AC = AD
AB is the bisector of ∠A
So, ∠BAC = ∠DAB
TO PROVE: ΔABC≅ΔABD
PROOF: In ΔABC and ΔABD
We have
AC = AD (given)
AB = AB (common)
∠BAC = ∠DAB (given)
ΔABC≅ΔABD (SAS rule)
BC = BD (by CPCT)
Q2. ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (see the given figure ).Prove that
(i) ΔABD ≅ΔBAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC
Ans.
(i) GIVEN: ABCD is a quadrilateral
AD = BC and ∠DAB = ∠CBA
TO PROVE: ΔABD ≅ΔBAC
PROOF: In ΔABD and ΔBAC
AD = BC (given)
AB = AB (common)
∠DAB = ∠CBA
ΔABD ≅ΔBAC (SAS)
Hence proved
(ii) BD = AC (By CPCT)
(iii) ∠ABD = ∠BAC(By CPCT)
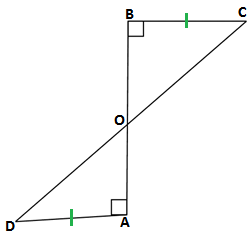
Q3. AD and BC are equal perpendiculars to a line segment AB (see the given figure).Show that CD bisects AB.
Ans.
GIVEN: AD = BC
AB ⊥ BC and AB ⊥ BC
∴∠OBC = ∠OAD = 90°
TO PROVE: CD bisects AB i.e AO = BO
PROOF: In ΔAOD and ΔBOD
Since BOA and COD is a line
∠DOA = ∠BOC (vertically opposite angle)
AD = BC (Given)
∠OBC = ∠OAD = 90°(given)
ΔBOC ≅ ΔAOD(AAS)
AO = BO (By CPCT)
Hence Proved
See the video for the solutions of Q1 TO Q3
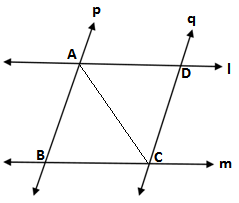
Q4. l and m are two parallel lines intersected by another pair of parallel lines p and q(see the given figure). Show that ΔABC ≅ CDA.
Ans.
GIVEN: p ∥ q and l∥ m
TO PROVE: ΔABC ≅ ΔCDA
PROOF:In the figure
l∥ m and AC is the transversal(given)
So, ∠DAC = ∠ACB (alternate angles)
p ∥ q and AC is the transversal(given)
∠BAC = ∠ACD(alternate angles)
AC = AC(given)
ΔABC ≅ Δ CDA(ASA rule)
Hence proved
Q5.Line l is the bisector of an angle ∠A and B is any point on l ,BP and BQ are perpendiculars from B to the arms of ∠A(see the given figure). Show that
(i) ΔAPB ≅ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠A
Ans.
(i) GIVEN: ,BP and BQ are perpendiculars from B to the arms of ∠A
∴∠AQB = ∠APB = 90°
Line l is the bisector of an angle ∠A and
∴∠QAB = ∠PAB
TO PROVE: ΔAPB ≅ΔAQB
PROOF:∠AQB = ∠APB = 90°(given)
AB = AB (common)
∠QAB = ∠PAB (given)
ΔAPB ≅ΔAQB (AAS rule)
(ii) BP = BQ(by CPCT)
Hence proved
Q6. In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC =DE.
Ans.
GIVEN: AC = AE
AB = AD
∠BAD = ∠EAC
TO PROVE: BC =DE
PROOF: We have to prove BC =DE, which are sides of the triangle ΔABC and ΔADE
In triangles ΔABC and ΔADE
AB = AD(given)
AC = AE(given)
∠BAD = ∠EAC (given)
Adding both sides ∠DAC
∠BAD + ∠DAC = ∠EAC + ∠DAC
∠BAC = ∠DAE(proved)
ΔABC ≅ ΔADE (SAS rule)
BC = DE (by CPCT )
Hence proved
See the video for the solutions of Q4 TO Q6
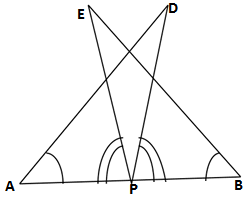
Q7. AB is a line segment and p is its midpoint. D and E are points on the same sides of AB such that ∠BAD = ∠ABE and ∠EPA=∠DPB(see the given figure). Show that
(i) ΔDAP≅ ΔEBP
(ii) AD = BE
Ans.(i)
GIVEN: ∠DAP = ∠EBP
∠EPA = ∠DPB
P is the mid point of AB
∴AP = BP
TO PROVE:
(i) ΔDAP≅ ΔEBP
(ii) AD = BE
PROOF: In ΔDAP and ΔEBP
∠BAD = ∠ABE(given)
∠EPA=∠DPB(given)
Adding ∠EPD both sides
∠EPA +∠EPD =∠DPB+ ∠EPD
∠APD = ∠EPB
AP = BP(given)
ΔDAP≅ ΔEBP(ASA rule)
Q8.In right triangle ABC ,right angled at C , M is th mid point of hypotenuse AB, C is joined to M and produced to a point D such that DM = CM . Point D is joined to point B(see the given figure). Show that
(i) ΔAMC ≅ BMD
(ii) ∠DBC is a right angle
(iii) ΔDBC ≅ ΔACB
Ans.
(i) GIVEN:ΔABC is a right triagle ,∠C = 90°
M is the midpoint of AB
∴BM = AM
AM = AB/2
DM = CM
TO PROVE: ΔAMC ≅ BMD
PROOF:DM = CM (given)
BM = AM (given)
∠BMD = ∠AMC (Vertically opposite angle)
ΔAMC ≅ BMD(SAS rule)
Hence proved
(ii) Since ΔAMC ≅ BMD(proved)
∠DBM = ∠CAM (By CPCT)
∠DBM and ∠CAM are alternate angles
∴DB ∥ AC
∠DBC + ∠ACB = 180° (co-interior angles)
∠ACB = 90°
∠DBC + 90° = 180°
∠DBC = 90°
Hence proved
(iii) Since ΔAMC ≅ BMD(proved)
BD = AC (By CPCT)
BC = BC(common)
∠DBC = ∠ACB =90°(Proved above)
ΔDBC ≅ ΔACB (SAS rule)
proved above
(iv) CM = DM(given)
CM + DM = DC
CM + CM = DC
2CM = DC
CM = 1/2 DC
Since we have proved
ΔDBC ≅ ΔACB
So, DC = AB (by CPCT)
Therefore
CM = 1/2 AB
Hence proved
See the video of the solutions for question 7 and question 8
You can compensate us by donating any amount of money for our survival
Our Paytm NO 9891436286
Paytm number 9891436286
The money collected by us will be used for the education of poor students who leaves their study because of a lack of money.
NCERT Solutions of Science and Maths for Class 9,10,11 and 12
NCERT Solutions for class 9 maths
NCERT Solutions for class 9 science
NCERT Solutions for class 10 maths
CBSE Class 10-Question paper of maths 2021 with solutions
CBSE Class 10-Half yearly question paper of maths 2020 with solutions
CBSE Class 10 -Question paper of maths 2020 with solutions
CBSE Class 10-Question paper of maths 2019 with solutions
NCERT Solutions for Class 10 Science
NCERT Solutions for class 11 maths
| Chapter 1-Sets | Chapter 9-Sequences and Series |
| Chapter 2- Relations and functions | Chapter 10- Straight Lines |
| Chapter 3- Trigonometry | Chapter 11-Conic Sections |
| Chapter 4-Principle of mathematical induction | Chapter 12-Introduction to three Dimensional Geometry |
| Chapter 5-Complex numbers | Chapter 13- Limits and Derivatives |
| Chapter 6- Linear Inequalities | Chapter 14-Mathematical Reasoning |
| Chapter 7- Permutations and Combinations | Chapter 15- Statistics |
| Chapter 8- Binomial Theorem | Chapter 16- Probability |
CBSE Class 11-Question paper of maths 2015
CBSE Class 11 – Second unit test of maths 2021 with solutions
NCERT solutions for class 12 maths
| Chapter 1-Relations and Functions | Chapter 9-Differential Equations |
| Chapter 2-Inverse Trigonometric Functions | Chapter 10-Vector Algebra |
| Chapter 3-Matrices | Chapter 11 – Three Dimensional Geometry |
| Chapter 4-Determinants | Chapter 12-Linear Programming |
| Chapter 5- Continuity and Differentiability | Chapter 13-Probability |
| Chapter 6- Application of Derivation | CBSE Class 12- Question paper of maths 2021 with solutions |
| Chapter 7- Integrals | |
| Chapter 8-Application of Integrals |
Class 12 Solutions of Maths Latest Sample Paper Published by CBSE for 2021-22 Term 2
Class 12 Maths Important Questions-Application of Integrals
Solutions of Class 12 Maths Question Paper of Preboard -2 Exam Term-2 CBSE Board 2021-22
Solutions of class 12 maths question paper 2021 preboard exam CBSE Solution